Основные алгоритмы на графах

• Я не стану подробно описывать, что такое граф, так как полно других источников, но скажу, что задача из ОГЭ(ЕГЭ) по информатике на нахождение кратчайшего пути, это и есть граф.

• Держите ссылочку на основную информацию о графах: Графы
• Больше про терминологию в мире графов можно прочитать здесь

Поиск (Обход) в ширину | BFS

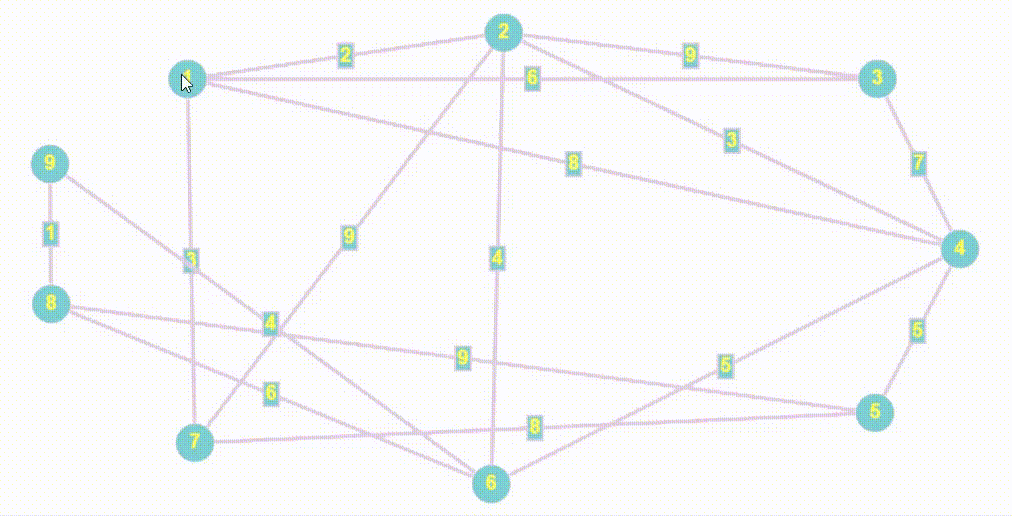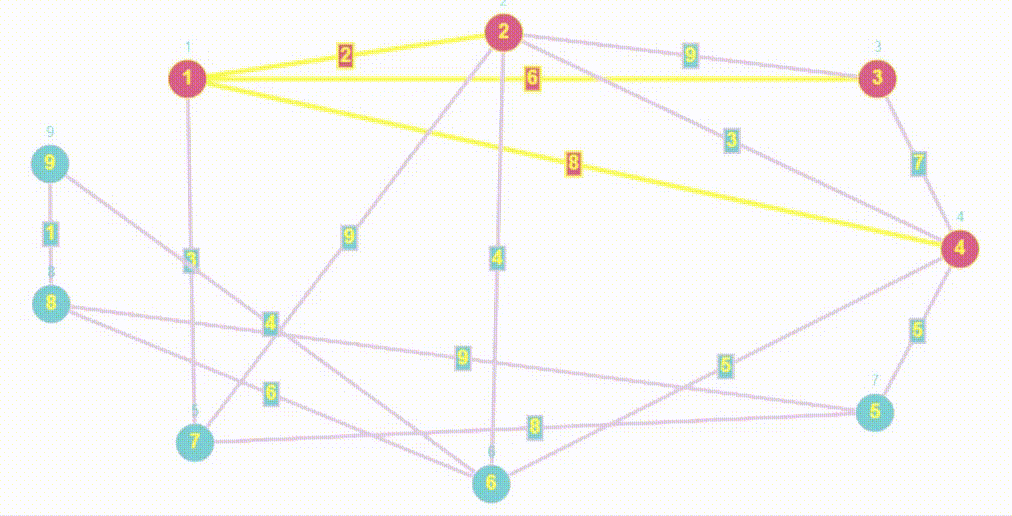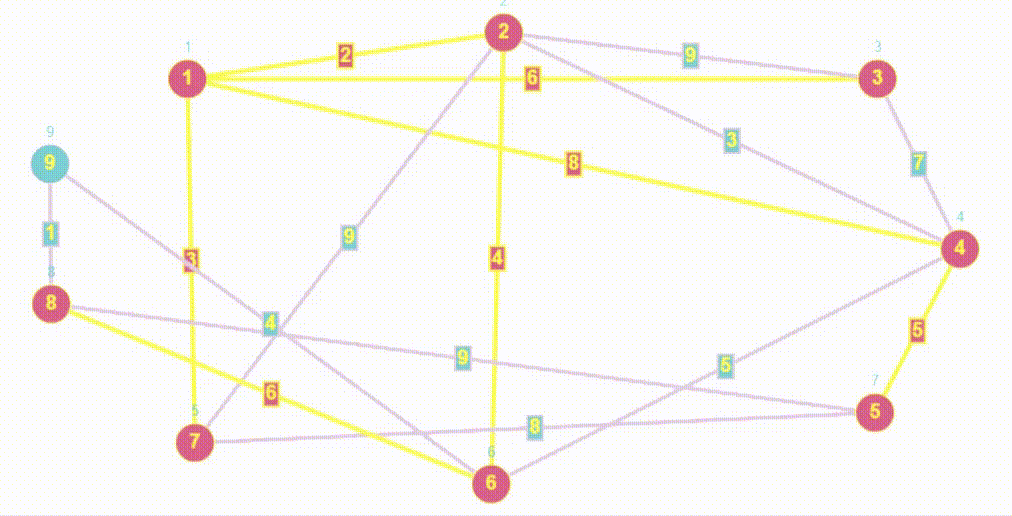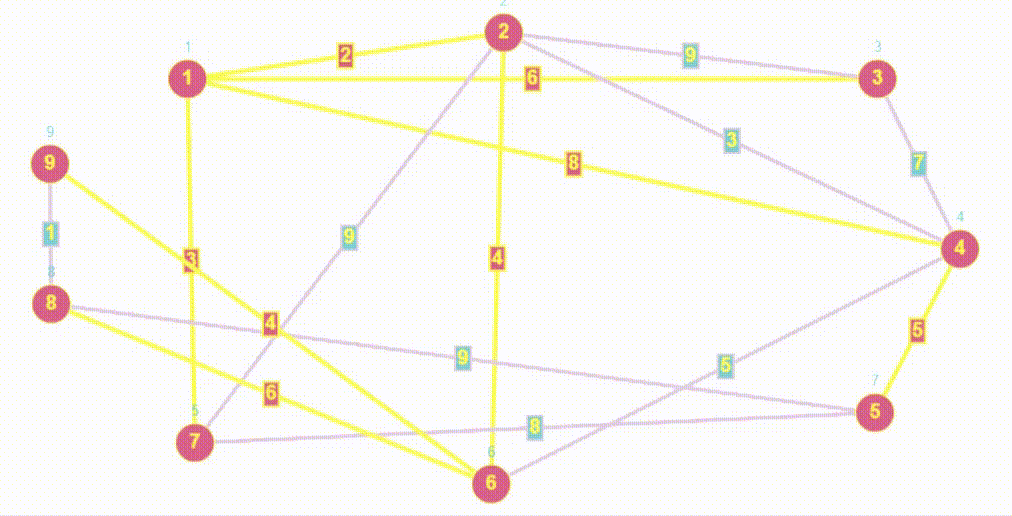
• Алгоритм BFS очень похож на Волновой алгоритм, так как волновой алгоритм относится к семейству алгоритмов основанных на методах поиска в ширину.
• Обход в ширину работает на основе очереди

Алгоритм

1. На вход в функцию BFS приходит граф и стартовая вершина
2. Возвращать BFS будет массив порядка посещения вершин (пометим как enter_order)
3. Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
4. Кладем в очередь нашу стартовую вершину и кладем в enter_order нашу стартовую вершину
5. Пока наша очередь
   5.1. Получаем элемент из очереди (пометим это как from) (в очереди хранится лишь порядковый номер вершины)
   5.2. Удаляем вытащенный элемент из очереди
   5.3. Перебирая все вершины графа:
   5.3.1. Если перебираемая вершина (пометим как to) непосещенная и по матрице смежности между from и to есть ребро, то
   5.3.1.1. Помечает вершину to как посещенную
   5.3.1.2. Кладем эту вершину в очередь и enter_order
   5.3.2. Иначе ничего не делаем
6. Возвращаем enter_order

Поиск (Обход) в глубину| DFS

• Основное отличие BFS от DFS только в том, что BFS используется очередь а DFS используется stack, в остальном алгоритм обхода практически не отличается
• Обычно все реализовывают рекурсивный обход в глубину, я распишу алгоритм итеративного обхода в глубину

Алгоритм

1. На вход в функция DFS приходит граф и стартовая вершина
2. Возвращать BFS будет массив порядка посещения вершин (пометим как enter_order)
3. Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
4. Кладем в стек нашу стартовую вершину и кладем в enter_order нашу стартовую вершину
5. Пока наш стек не пустой:
   5.1. Получаем элемент из стека (пометим это как from)
   5.2. Перебирая все вершины графа:
   5.2.1. Если перебираемая вершина (пометим как to) непосещенная и по матрице смежности между from и to есть ребро, то
   5.2.1.1. Помечаем вершину to как посещенную
   5.2.1.2. Кладем эту вершину в стек и в enter_order
   5.2.1.3. Присваиваем вершине from значение вершины to (Это нужно для того чтобы просматривать ребра в глубину)
   5.2.2. Иначе ничего не делаем
   5.3. Если условие 5.2.1 не выполнилось выполнилось, то удаляем из стека наш верхний элемент
6. Возвращаем enter_order

BFS

std::vector<int> BreadthFirstSearch(Graph &graph, int start_vertex) {   if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)     return {};    std::vector<int> enter_order;   std::vector<short> visited(graph.GetVertexesCount());   std::queue<int> q;    // Функция принимает вершину, нумерация которой начинается с 1   // Для удобства уменьшаем ее значение на 1, чтобы нумерация начиналась с 0   --start_vertex;   visited[start_vertex] = true;   q.push(start_vertex);   enter_order.emplace_back(start_vertex + 1);    while (!q.empty()) {     auto from = q.front();     q.pop();      for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {       if (!visited[to] and graph(from, to) != 0) {         visited[to] = true;         q.push(to);         enter_order.emplace_back(to + 1);       }     }   }    return enter_order; }

DFS

std::vector<int> DepthFirstSearch(Graph &graph, int start_vertex) {   if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)     return {};    std::vector<int> enter_order;   std::vector<short> visited(graph.GetVertexesCount());   std::stack<int> s;    --start_vertex;   visited[start_vertex] = true;   s.push(start_vertex);   enter_order.emplace_back(start_vertex + 1);    while (!s.empty()) {     auto from = c.top();     bool is_found = false;      for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {       if (!visited[to] and graph(from, to) != 0) {         is_found = true;         visited[to] = true;         s.push(to);         enter_order.emplace_back(to + 1);         from = to;       }     }      if (!is_found)       s.pop();   }    return enter_order; }

Заметим, что код практически ничем не отличается, поэтому их можно объединить в одну функцию, и передавать туда просто тип контейнера

// // If Container type = std::stack<int> it will be DepthFirstSearch // If Container type = std::queue<int> it will be BreadthFirstSearch // template <typename Container = std::stack<int>> std::vector<int> FirstSearch(Graph &graph, int start_vertex) {   if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)     return {};    constexpr bool is_stack = std::is_same_v<Container, std::stack<int>>;    std::vector<int> enter_order;   std::vector<short> visited(graph.GetVertexesCount());   Container c;    --start_vertex;   visited[start_vertex] = true;   c.push(start_vertex);   enter_order.emplace_back(start_vertex + 1);    while (!c.empty()) {     int from = -1;     if constexpr (is_stack) from = c.top();     else {       from = c.front();       c.pop()     }      bool is_found = false;      for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {       if (!visited[to] and graph(from, to) != 0) {         is_found = true;         visited[to] = true;         c.push(to);         enter_order.emplace_back(to + 1);         if (is_stack)           from = to;       }     }      if (is_stack and !is_found)       c.pop();   }    return enter_order; }

• Тогда код BFS & DFS будет выглядеть так:

std::vector<int> BreadthFirstSearch(Graph &graph, int start_vertex) {   return FirstSearch<std::queue<int>>(graph, start_vertex); }  std::vector<int> DepthFirstSearch(Graph &graph, int start_vertex) {   return FirstSearch<std::stack<int>>(graph, start_vertex); }

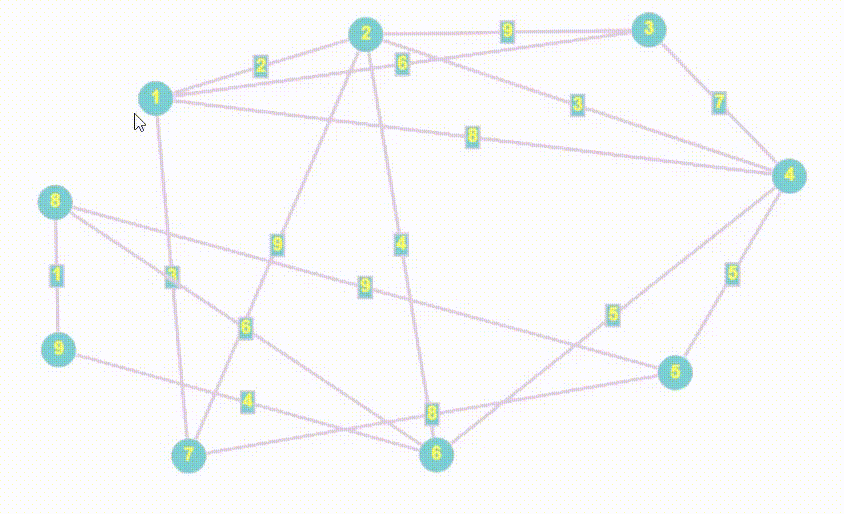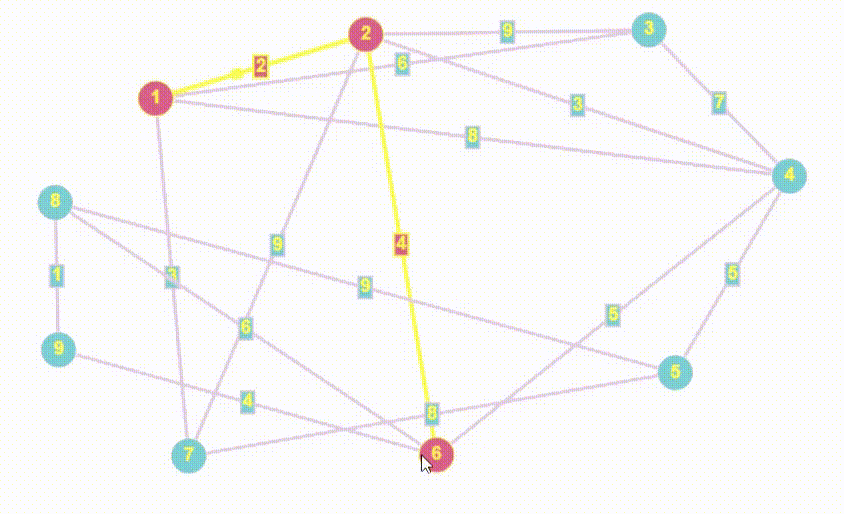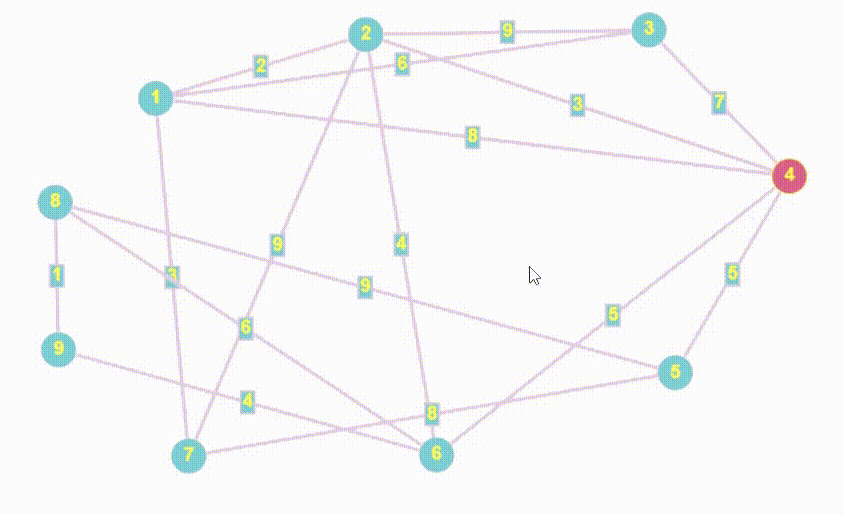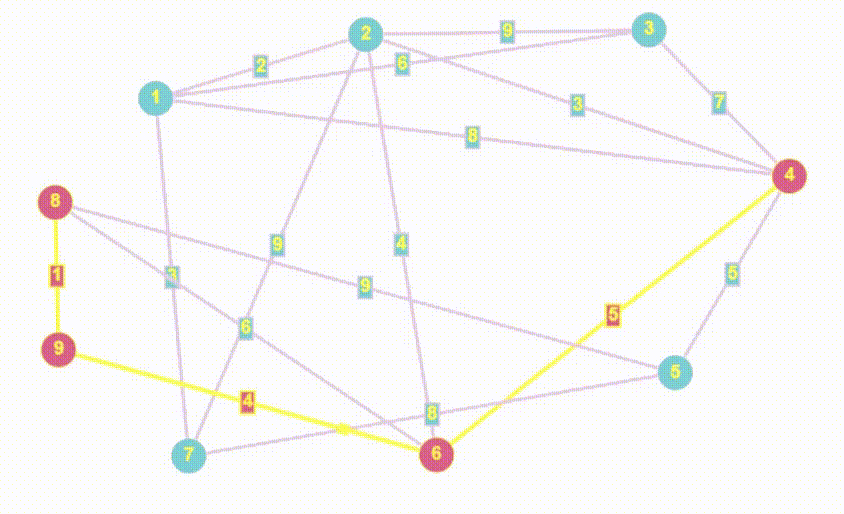
• Алгоритм Дейкстры принципом работы очень похож на BFS
• Полный алгоритм Дейкстры возвращает массив кратчайших расстояний от стартовой точки до всех остальных, мы найдем все расстояния, но вернем лишь то, которое хочет пользователь
• Единственным минусом алгоритма Дейкстры являемся, неумение работать с отрицательными весами ребер

Алгоритм

1. На вход функция Алгоритма Дейкстры будет принимать граф и две вершины, стартовая (пометим как start) и конечная (пометим как finish)
2. Создадим массив длин от start до всех остальных вершин (пометим как distance), изначально пометим все длины в массиве бесконечностью.
3. Стартовую точку в distance пометим как 0, потому что расстояние от точки, до самой точки равно нулю (в данном алгоритме мы не рассматриваем ситуации когда есть петли)
4. Создаем множество из пары значений, пара будет хранить длину и индекс вершины
5. Инициализируем наше множество стартовым значением, за стартовое значение отвечает стартовая вершина, поэтому в множестве будет лежать: длина -> 0 и индекс start
6. Пока наше множество не пусто:
   6.1. Получаем начальный элемент в множестве (пометим как from) (вспоминаем, что в множестве хранится пара значений, нам нужен лишь индекс вершины)
   6.2. Удаляем начальный элемент из множества
   6.3. Перебирая все вершины графа:
   6.3.1. Если между from и перебираемой вершиной (пометим как to) есть ребро
   6.3.2. И если расстояние от start до to больше чем расстояние от start до from + вес самого ребра (from, to)
   6.3.2.1. Удаляем из множества старую пару значений: {расстояние от start до to, индекс вершины to}
   6.3.2.2. В distance обновляем расстояние от start до to на более короткое, которое мы проверяли в условии 6.3.2
   6.3.2.3. Вставляем в множество обновленную пару: {расстояние от start до to, индекс вершины to}
7. Возвращаем из массива distance расстояние под индексом finish

int GetShortestPathBetweenVertices(Graph &graph, int start, int finish) {   if (start <= 0 or finish <= 0 or start > graph.GetVertexesCount() or finish > graph.GetVertexesCount())     return kInf;    std::vector<int> distance(graph.GetVertexesCount(), kInf);    --start, --finish;   distance[start] = 0;    std::set<std::pair<int, int>> q;   q.insert({distance[start], start});    while (!q.empty()) {     auto from = q.begin()->second;     q.erase(q.begin());      for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {       bool edge_is_exists = graph(from, to) != 0;       bool new_edge_is_shorter = distance[to] > distance[from] + graph(from, to);        if (edge_is_exists and new_edge_is_shorter) {         q.erase({distance[to], to});         distance[to] = distance[from] + graph(from, to);         q.insert({distance[to], to});       }     }   }    return distance[finish]; }

По коду можно увидеть явные признаки схожести с BFS, я даже специально множество назвал как q, потому что в данном случае множество отыгрывает роль псевдо-очереди

• Алгоритм Флойда-Уоршелла — это алгоритм поиска кратчайших путей во взвешенном и не взвешенном графе с положительным или отрицательным весом ребер (но без отрицательных циклов). За одно выполнение алгоритма будут найдены длины (суммарные веса) кратчайших путей между всеми парами вершин.
• Логично что алгоритм будет возвращать матрицу расстояний между всеми парами вершин (грубо говоря новую матрицу смежности)
• Алгоритм не содержит детали о самих кратчайших путях, а запоминает лишь кратчайшее расстояние, но алгоритм можно усовершенствовать, ссылка на видео здесь, да и описание вместе с реализацией можно посмотреть там же.
• Сложность алгоритма независимо от типа графа O(V^3), где V — количество вершин

Алгоритм

1. На вход функция Алгоритма Флойда-Уоршелла будет принимать только сам граф
2. Создаем копию матрицы смежности графа (пометим как distance)
   2.1. Основное отличие distance от той, которая лежит в графе лишь в том, что все нули в матрице смежности графа, в матрице distance будут бесконечностью (кроме главной диагонали), так как главная диагональ хранит в себе расстояние от вершины до самой себя, поэтому и ноль (мы не учитываем ситуации с петлями, предположим что их нет)
3. Постепенно открывая доступ к вершинам (открытие доступа к вершине означает, что мы просто перебираем все вершины с индексами от 0 до V — 1 (конечно же, если индексация нулевая)), пусть вершина, к которой открыли доступ называется v:
   3.1. Просматривая все возможные и невозможные ребра в графе (в двух циклах пробегаемся по матрице distance), пусть счетчик внешнего цикла будет называться row, а счетчик вложенного цикла будет называться col:
   3.1.1. Получаем суммарный вес ребер {row, v} и {v, col}
   3.1.2. Если ребро {row, v} и ребро {v, col} существуют и текущее значение в матрице distance под индексами {row, col} больше чем суммарный вес двух новых ребер, то:
   3.1.2.1. Обновляем в матрице distance расстояние на более короткое, которое мы вычислили в пункте 3.1.1
   3.1.3. Иначе ничего не делаем
4. Возвращаем матрицу distance

Matrix<int> GetShortestPathsBetweenAllVertices(Graph &graph) {   const int vertexes_count = graph.GetVertexesCount();   Matrix<int> distance(vertexes_count, vertexes_count, kInf);    // Пункт 2   for (int row = 0; row != vertexes_count; ++row) {     for (int col = 0; col != vertexes_count; ++col) {       distance(row, col) = graph(row, col) == 0 ? kInf : graph(row, col);       if (row == col)         distance(row, col) = 0;     }   }    // Пункт 3 (Постепенно открываем доступ к новым вершинам)   for (int v = 0; v != vertexes_count; ++v) {     // Пункт 3.1 (Пробегаемся по матрице distance)     for (std::size_t row = 0; row != vertexes_count; ++row) {       for (std::size_t col = 0; col != vertexes_count; ++col) {         int weight = distance(row, v) + distance(v, col);         if (distance(row, v) != kInf and distance(v, col) != kInf and distance(row, col) > weight)           distance(row, col) = weight;         }       }     }    return distance; }

Написать реализацию гораздо проще, чем понять как этот алгоритм работаем, поэтому советую ознакомиться с видео

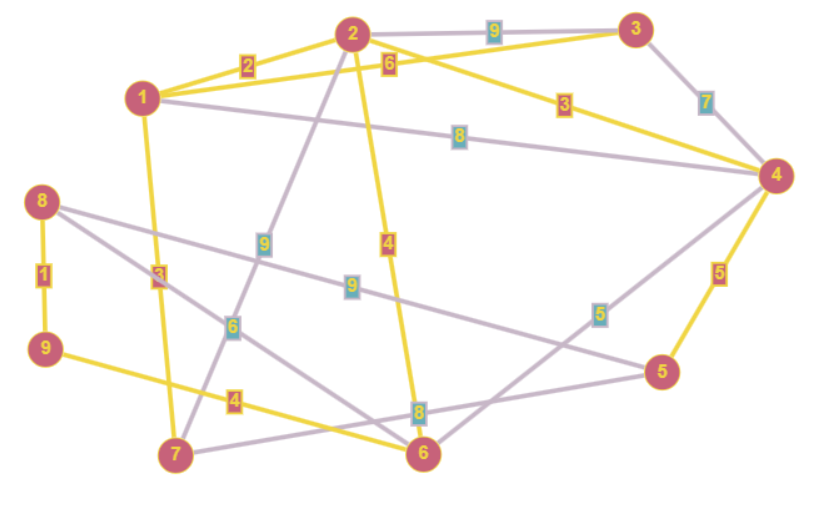
• Алгоритм Прима — алгоритм который находит минимальное остовное дерево в графе, минимальное значит, что сумма весов ребер стремится к нулю (если это возможно)
• Алгоритм Прима работает с неориентированными графами, поэтому если нам был передам ориентированный граф, мы будем игнорировать направление ребер.
• Остовное дерево должно включать в себя все вершины графа
• Каждая вершина должна быть посещена ровно 1 раз
• Результатом работы Алгоритма прима будет матрица смежности дерева

Скажу сразу, что моя реализация не умеет работать с графами у которых, есть изолированные вершины, как только я это сделаю я изменю статью, спасибо за понимание.

Алгоритм

1. Создаем два множеств, для посещенных и не посещенных вершин (пометим, соответственно, как visited и unvisited)
2. Создаем исходную матрицу, которая будет представлять собой остовное дерево (пометим как spanning_tree)
3. Создаем массив ребер (пометим как tree_edges), ребро в данном случае это структура, которая хранит две вершины и вес самого ребра.
4. Инициализируем множество непосещенных вершин всеми, существующими в графе вершинами
5. Выбираем, случайным образом, вершину, от которой будет строиться остовное дерево, и помечаем эту вершину как посещенной, соответственно из множества непосещенных ее убираем
6. Пока множество непосещенных першин не пусто:
   6.1. Создаем ребро инициализируя его поля бесконечностями
   6.2. Перебирая все посещенные вершины (пометим как from):
   6.2.1. Перебираем все вершины графа (пометим как to):
   6.2.1.1. Если to является непосещенной вершиной и ребро между вершинами {from, to} существует и вес ребра (созданного в пункте 5.1) больше чем вес ребра между вершинами {from, to}, то:
   6.2.1.1.1. Обновляем ребро (5.1) вершинами from и to и весом между этими вершинами
   6.3. Если вес ребра не равен бесконечности:
   6.3.1. Добавляем в массив tree_edges новое ребро
   6.3.2. Удаляем из множества непосещенных вершин вершину to
   6.3.3. Добавляем в множество посещенных вершин вершину to
   6.3.4. Иначе прекращаем цикл
7. Пробегаясь по всем ребрам массива tree_edges:
   7.1. Инициализируем spanning_tree, добавляя в нее ребра (добавлять нужно в обе стороны, чтобы граф получился неориентированным)
8. Возвращаем spanning_tree

Matrix<int> GraphAlgorithms::GetLeastSpanningTree(Graph &graph) {     const auto vertexes_count = graph.GetVertexesCount();      Matrix<int> spanning_tree(vertexes_count, vertexes_count, kInf);     std::set<int> visited, unvisited;     std::vector<Edge> tree_edges;      for (int v = 0; v != vertexes_count; ++v)         unvisited.insert(v);      {         // Вершина должна браться случайно, но какая разница, если дерево статичное.         // Дерево независимо от start_vertex всегда одинаковое         const auto start_vertex = static_cast<int>(vertexes_count / 2);         visited.insert(start_vertex);         unvisited.erase(start_vertex);     }      // Initialize Finish -> Start main loop      while (!unvisited.empty()) {         Edge edge(kInf, kInf, kInf);          for (const auto &from : visited) {             for (int to = 0; to != vertexes_count; ++to) {                  bool is_unvisited_vertex = unvisited.find(to) != unvisited.end();                 bool edge_is_exists = graph(from, to) != 0 or graph(to, from) != 0;                  if (edge_is_exists and is_unvisited_vertex) {                     int existed_weight = graph(from, to) == 0 ? graph(to, from) : graph(from, to);                     bool edge_is_shorter = edge.weight > existed_weight;                      if (edge_is_shorter)                         edge = {from, to, existed_weight};                 }             }         }          if (edge.weight != kInf) {             tree_edges.emplace_back(edge);             visited.insert(edge.vertex2);             unvisited.erase(edge.vertex2);         } else {             break;         }     }      // Initializing spanning tree      for (const auto &edge : tree_edges) {         spanning_tree(edge.vertex1, edge.vertex2) = edge.weight;         spanning_tree(edge.vertex2, edge.vertex1) = edge.weight;     }      return spanning_tree; }