Что под капотом у нейронной сети. Нейросеть c точки зрения математики и программирования

Здравствуйте, меня зовут Александр, я backend-разработчик.

Часто искусственные нейронные сети рассматриваются или с точки зрения математических моделей, или с точки зрения написания программ на конкретном языке. Как в притче о слоне и слепых мудрецах.

Цель данной публикации – комплексное рассмотрение строения искусственных нейронных сетей c точки зрения и математики и программного кода. В данной работе нейронная сеть реализуется на языке Python с использованием библиотеки tensorflow.keras. Статья сосредоточена в основном на строении и функционировании искусственной нейронной сети, поэтому такие этапы как обучение и т.д. в ней не затрагиваются.

Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Так, все они, так же, как и мозг человека, состоят из большого числа связанных между собой однотипных элементов – нейронов, которые имитируют нейроны головного мозга. С точки зрения математики, в нейронной сети каждый нейрон представляет из себя функцию, зависящую от значений входных сигналов, весов этих сигналов и некой активационной функции.

Прежде всего необходимо остановиться на понятии активационной функции. Она может быть представлена в виде любой функцией от нескольких аргументов, возвращающей одно значение. Данная функция нужна, чтобы определить при каких входных значениях должен включаться (активироваться) нейрон, т.е. проводить сигнал. А при каких нет. Чаще всего используются следующие функции:

1. Линейная функция активации который имеет вид

2. Сигмоид который имеет вид

3. ReLu вида

   В расчетах будем использовать активационную функцию ReLu с параметром a = 1. Т.к. активационная функция имеет вид f(x) = x, для положительных значений параметров ей можно пренебречь.

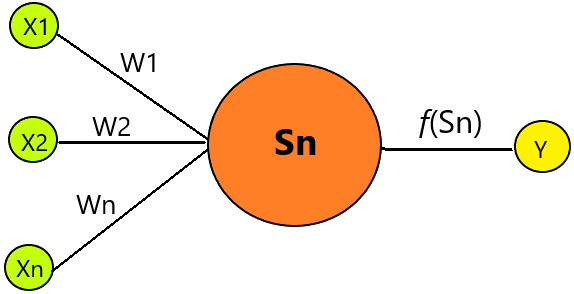
   Вернемся к строению нейрона. На каждый вход нейрона подаются значения (X), которые затем распространяются по межнейронным связям (синапсисам). У синапсов есть один параметр — W (вес), благодаря которому входная информация изменяется при переходе от одного нейрона к другому.

   

   X1 … Xn – значение входных сигналов, Y – выходной сигнал, W1…Wn – вес определяет, насколько соответствующий вход нейрона влияет на его состояние.

   Таким образом нейрон так же представляет из себя некую функцию вида

   

   где f – активационная функция.

   Таким образом, искусственная нейронная сеть – это линейный многочлен со множеством параметров.

   Рассмотрим пример. Исследуется зависимость Y от двух параметров X1 и X2.

   В ходе неких экспериментов получены следующие зависимости.

   X1	X2	Y
   1	1	2
   2	1	3
   3	1	4
   4	1	5
   5	1	6
   1	2	3
   2	2	4
   3	2	5
   4	2	6
   5	2	7
   1	5	6

   Не сложно заметить, что зависимость
   Но допустим, мы этого не знаем. Попробуем найти значения Y обучив нейронную сеть.

   Мы построим несколько видов нейросетей (с разным числом нейронов), а затем с помощью библиотеки keras в python найдем нужные веса. Для расчетов будет использоваться многослойная нейронная сеть.

   from tensorflow.keras.models import Sequential model = Sequential()

   Для нахождения весов на каждом слое используется команда

   for layer in model.layers:    print(layer.get_weights())

   Рассмотрим две схемы нейронной сети:

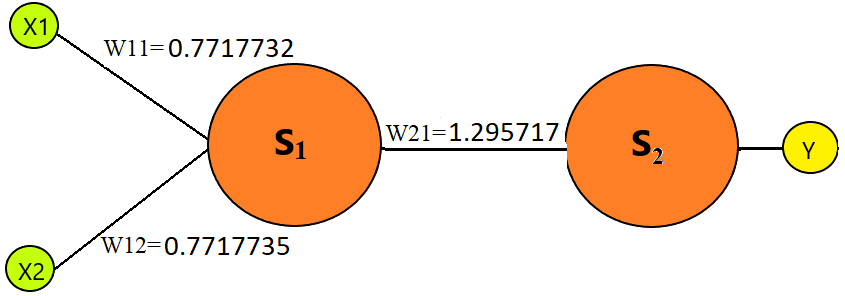
   В первом случае нейронная сеть имеет два слоя, на каждом слое по одному нейрону (вычисленный вес показан на рисунке).

   

   model.add(Dense(1, input_shape=X.shape[1:], kernel_constraint=non_neg())) model.add(layers.Activation(keras.activations.relu)) model.add(Dense(1, activation='linear', kernel_constraint=non_neg()))

   Выполним проверку, т.е. вычислим многочлен Y = (X1 * W11 + X2 * W12) * W21

   Для получения аналогичных данных используется метод predict

   model.predict(…)

   X1	X2	Y = X1 + X2	Вычисленный результат
   1	1	2	(1*0.7717732 + 1*0.7717735)*1.295717 = 2
   10	10	20	(10*0.7717732 + 10*0.7717735)*1.295717 = 20
   5.5	2.5	8	(5.5*0.7717732 + 2.5*0.7717735)*1.295717 = 8
   10.3	2.1	12.4	(10.3*0.7717732 + 2.1*0.7717735)*1.295717 = 12.4
   8.3	20.1	28.4	(8.3*0.7717732 + 20.1*0.7717735)*1.295717 = 28.4

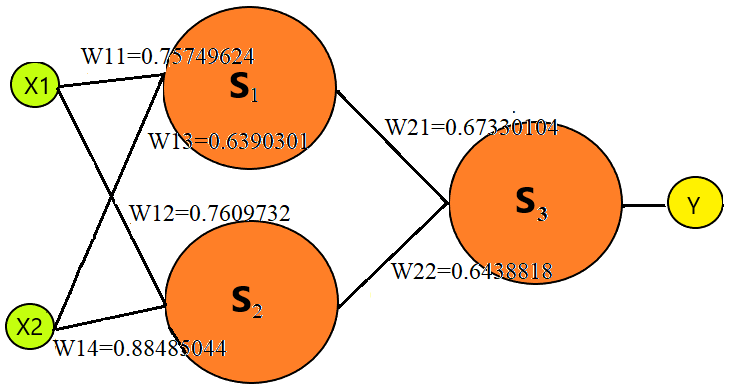
   Во втором случае нейронная сеть имеет два слоя, на первом слое два нейрона, а на втором они нейрон (вычисленный вес показан на рисунке).

   

   model.add(Dense(1, input_shape=X.shape[1:], kernel_constraint=non_neg())) model.add(layers.Activation(keras.activations.relu)) model.add(Dense(1, activation='linear', kernel_constraint=non_neg()))

   Вычислим многочлен Y = (X1 * W11 + X2 * W12) * W21 + (X1 * W13 + X2 * W14) * W22

   X1	X2	Y = X1 + X2	Вычисленный результат
   1	1	2	(1*0.75749624 + 1*0.7609735)* 0.67330104 + (1*0.6390331+ 1* 0.88485044)*0.6438818 = 2
   10	10	20	(10* 0.75749624 + 10* 0.7609735)*0.67330104 + (10* 0.6390331+ 10* 0.88485044)*0.6438818 = 20
   5.5	2.5	8	(5.5* 0.75749624 + 2.5* 0.7609735)*0.67330104 + (5.5* 0.6390331+ 2.5* 0.88485044)*0.6438818 = 8
   10.3	2.1	12.4	(10.3* 0.75749624 + 2.1* 0.7609735)*0.67330104 + (10.3* 0.6390331+ 2.1* 0.88485044)*0.6438818 = 11.76
   8.3	20.1	28.4	(8.3* 0.75749624 + 20.1* 0.7609735)0.67330104 + (8.3 0.6390331+ 20.1* 0.88485044)*0.6438818 = 29.4

   Итак, мы рассмотрели строение нейрона и простейших нейронных сетей, которые, с точки зрения математики, представляют из себя многочлены с большим числом параметров (весов). Обучение нейронной сети как раз представляет из себя нахождение этих параметров.