Точка пересечения двух отрезков

Введение

Уже не раз на habr затрагивалась данная тема: раз, два.

Я лишь хочу поделиться своей реализацией. Думаю, это кому-то пригодится.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Подготовка

Весь последующий код будет приведён на языке Java

Для начала создадим вспомогательный класс Dot. В нём всего две переменные x и y:

static class Dot {         float x,y;         Dot(float x, float y){             this.x =x;             this.y = y;         }      @Override         public String toString() {             return "x:"+x+" y:"+y;         }     }

И класс Vector2. В нём всего две функции: crs (cross) — векторное произведение, scl (scale) — масштабирование вектора.

public static class Vector2 {         float x,y;          public Vector2(Dot d1, Dot d2) {             this.x = d2.x-d1.x;             this.y = d2.y-d1.y;         }          /** Calculates the 2D cross product between this and the given vector.          * @param v2 the other vector          * @return the cross product (Z vector) */         public static float crs(Vector2 v1, Vector2 v2) {             return v1.x * v2.y - v1.y * v2.x;         }          /** Multiplies this vector by a scalar */         public Vector2 scl (float scalar) {             x *= scalar;             y *= scalar;             return this;         } }

Задача 1: определить, касаются ли отрезки.

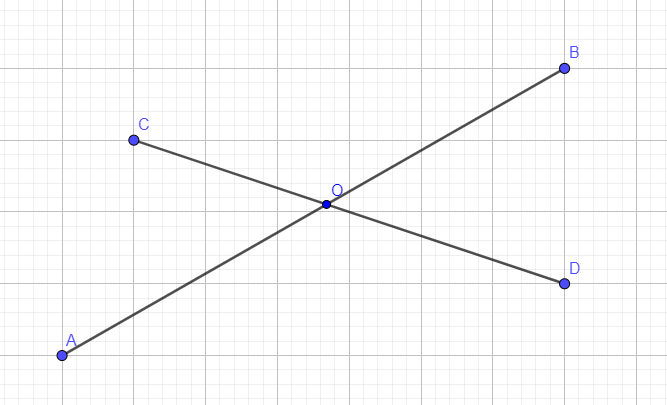
Решение:
Из векторного произведения мы можем узнать, обхо́дим мы вектор по часовой или против часовой. Это поможет понять где находятся точки. Соединим точки A и D, A и C.

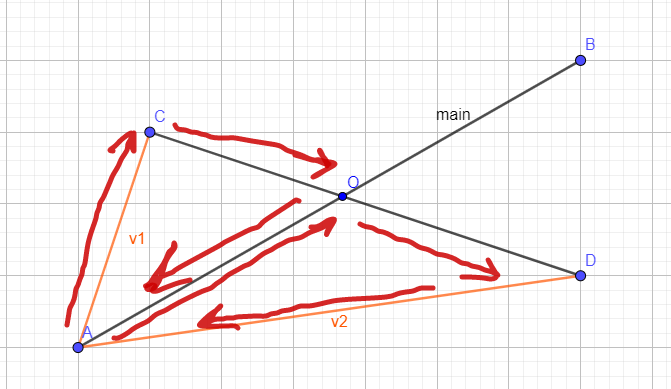
Перемножим вектора main и v2, main и v1. Если полученные произведения имеют разные знаки, значит точки C и D находятся по разные стороны относительно отрезка AB. Назовём такой метод fromDifferentSides:

public static boolean fromDifferentSides(Vector2 main, Vector2 v1, Vector2 v2){     float product1 =crs(main ,v1), product2 = crs(main ,v2);     return (product1>=0&&product2<=0 || product1<=0&&product2>=0); }

Таким же образом необходимо проверить точки A и B относительно отрезка CD. Соединим это в один метод и получится следующее:

public static boolean linesIntersect(Dot a, Dot b, Dot c, Dot d) {     Vector2 main = new Vector2(a,b);     Vector2 v1 = new Vector2(a,c);     Vector2 v2 = new Vector2(a,d);      if (fromDifferentSides(main,v1,v2)) {       main = new Vector2(c,d);       v1 =new Vector2(c,a);       v2 =new Vector2(c,b);       return fromDifferentSides(main,v1,v2);     }     return false; }

Задача 2: определить точку касания.

Решение:
Как и в предыдущей задаче определяем, касаются ли отрезки. Если касаются, начинаем определять эту точку. Через подобие найдём длину DO. Коэффициент подобия (k) равен отношению уже известных нам векторных произведений:

//коэффициент подобия double k = Math.abs(product2 / product1); if (Float.isInfinite((float) k)) return c;

В третей строчке проверяем пограничный случай. Теперь узнаем чему равно DO. Для этого решим систему уравнений:

DO = CO*k
Подставляем во второе уравнение:
CO*k+CO = CD
CO(k+1)= CD
CO = CD/(k+1)
В итоге:
DO = (CD/(k+1))*k

Теперь создаём вектор CD и уменьшаем его до длинны DO. Но поскольку мы будем его умножать, нужно взять обратное от (k+1)*k:

//вектор DC Vector2 dc = new Vector2(d, c);  //уменьшаем вектор dc.scl((float) (1 / (k + 1)*k));

Теперь осталось добавить вектор к точке D:

//добавляем вектор к точке return new Dot(d.x + dc.x, d.y + dc.y);

Вот и всё! Мы получили заветную точку.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Функцию нахождения точки я назвал pointOfIntersection. Привожу полный код на Java:

 public class Main {     public static void main(String[] args) {         System.out.println(pointOfIntersection(new Dot(0, 0),new Dot(5, 0), new Dot(2, 3),new Dot(2, 0) ));     }      public static Dot pointOfIntersection(Dot a, Dot b, Dot c, Dot d) {          Vector2 main = new Vector2(c,d);         Vector2 v1= new Vector2(c,a);         Vector2 v2 = new Vector2(c,b);         if (fromDifferentSides(main,v1,v2)) {             main = new Vector2(a,b);             v1 = new Vector2(a,c);             v2 = new Vector2(a,d);              double product1 = crs(main ,v1), product2 = crs(main ,v2);             if (product1>=0&&product2<=0 || product1<=0&&product2>=0) {                 //коэффициент подобия                 double k = Math.abs(product2 / product1);                 if (Float.isInfinite((float) k)) return c;                  //вектор DC                 Vector2 dc = new Vector2(d, c);                  //уменьшаем вектор                 dc.scl((float) (1 / (k + 1)*k));                  //добавляем вектор к точке                 return new Dot(d.x + dc.x, d.y + dc.y);             }          }          return null;     }      public static boolean linesIntersect(Dot a, Dot b, Dot c, Dot d) {         Vector2 main = new Vector2(a,b);         Vector2 v1 = new Vector2(a,c);         Vector2 v2 = new Vector2(a,d);          if (fromDifferentSides(main,v1,v2)) {             main = new Vector2(c,d);             v1 =new Vector2(c,a);             v2 =new Vector2(c,b);             return fromDifferentSides(main,v1,v2);         }         return false;     }      static class Dot {         float x,y;         Dot(float x, float y){             this.x =x;             this.y = y;         }          @Override         public String toString() {             return "x:"+x+" y:"+y;         }     }       public static class Vector2 {         float x,y;          public Vector2(Dot d1, Dot d2) {             this.x = d2.x-d1.x;             this.y = d2.y-d1.y;         }          /** Calculates the 2D cross product between this and the given vector.          * @param v2 the other vector          * @return the cross product (Z vector) */         public static float crs(Vector2 v1, Vector2 v2) {             return v1.x * v2.y - v1.y * v2.x;         }          /** Multiplies this vector by a scalar */         public Vector2 scl (float scalar) {             x *= scalar;             y *= scalar;             return this;         }          public static boolean fromDifferentSides(Vector2 main, Vector2 v1, Vector2 v2){             float product1 =crs(main ,v1), product2 = crs(main ,v2);             return (product1>=0&&product2<=0 || product1<=0&&product2>=0);         }        //функция округления         public static double round(double value, int places) {             if (places < 0) throw new IllegalArgumentException();             BigDecimal bd = new BigDecimal(Double.toString(value));             bd = bd.setScale(places, RoundingMode.HALF_UP);             return bd.doubleValue();         }     } } 

Надеюсь, вам понравилось. Удачи!