Ансамбль слоистых сред

Говорят, что жизнь как зебра: полоса черная, полоса белая, полоса черная, полоса белая…

Неизвестный философ.

Введение

Ах, если бы это было так, то зная где упасть, можно было бы и подстелить соломки перед наступлением черной полосы. Но чередование белых и черных полос, как и их продолжительность, непредсказуемы. Больше похоже на штрих код. Вот такой полосатый штрих код, только в применении к задачам геофизики я и стал рассматривать в качестве простого примера, разбираясь с книгой «Сейсмоакустика пористых и трещиноватых геологических сред».

Оказывается, уравнения распространения волн в среде со случайным распределением трещин или в пористых материалах могут быть «усреднены» с помощью диаграммной техники из квантовой теории поля и Юрий Александрович Кухаренко эту технику активно продвигал. Казалось бы, какая связь между квантами и трещинами? Это я и решил выяснить. Книжку читать оказалось не просто. Видно, что авторы хорошо разбираются и в квантовой теории поля, и в теории вероятностей, и в геофизике. А читателю приходится с карандашом анализировать все появляющиеся там формулы. Карандаш очень пригодился в разделе о математическом описанию случайности случайных сред. Все начинается очень абстрактно, по Колмогорову. Вводится вероятностное пространство, мера, и всевозможные функционалы. Для лучшего восприятия, я все концепции этого раздела применил к ансамблю случайных слоистых сред — те самые зебры-штрих-коды из вступительной части. Получилось очень педагогично, на мой взгляд.

От аксиом к примерам

Абстрактный подход к случайным слоистым средам начинается с аксиом теории вероятностей:

Случайные величины обозначаются буквами с крышечками, как операторы в квантовой механике - и это не с проста. Ведь сама по себе случайная величина, как и оператор, нам не доступны для наблюдения. Мы можем "видеть", например, их средние значения, а более правильней - экспериментальные "частоты". — Случайные величины обозначаются буквами с крышечками, как операторы в квантовой механике — и это не с проста. Ведь сама по себе случайная величина, как и оператор, нам не доступны для наблюдения. Мы можем «видеть», например, их средние значения, а более правильней — экспериментальные «частоты».

Чтобы понять, что стоит за этими весьма общими словами начнем конструировать пример. Итак, пусть у нас есть слоистый материал, составленный из слоев двух типов — трещина и остов пишу про слои, чтобы потом воспользоваться этим примером в расчете акустических свойств такого материала. Случайное поле и его реализация

$\eta(x,\hat \omega),\quad \eta(x)$

определяют то, что мы увидим в точке х : остов, если значение поля 1 и трещину, если значение поля 0.

Для начала я взял фиксированной толщину каждого слоя — обозначим ее d, хотите−пусть будет 1. С одной стороны это сильно упростило пример, а с другой стороны, если взять d очень маленьким, то из нескольких таких слоев можно составить слой любой толщины. Общее число слоев N я зафиксировал.

Что будет пространством событий в данном случае? Это множество, элементами которого являются возможные реализации слоистой структуры. Поставим в соответствие трещине 0 — пуста она, и потому нулем решил ее я обозначить, а остову сопоставим 1. Тогда пространство событий можно представить как множество W двоичных последовательностей w длины N. Если мы введем своими собственными руками аксиому — вероятность появления трещины в любом слое равна 0<t<1, и не зависит от других слоев, то вероятность последовательности w будет просто произведение

$P(w)=t^{n_0}(1-t)^{N-n_0}$

Здесь n₀ это число трещин! Вместо интеграла по вероятностной мере будет сумма по вероятностям всех событий из интересующего нас подмножества.

Если же мы по какой-то причине хотим вычислить вероятность появления «поля трещин», произвольно распределенного на интервале

$\eta(x),\qquad x\in(0,Nd),$

то скорее всего, получим ноль. Ненулевые значения будут только при условии, что распределение трещин согласовано с выбранной толщиной трещины/остова.

Функции распределения

Если мы вдруг захотим рассмотреть бесконечно-много бесконечно тонких случайно распределенных слоев, то возникнет проблема — вероятность попасть в какую-то реализацию будет стремиться к нулю. Нужно математически описать, как теперь нам измерять вероятность на разных множествах — то есть задать меру. Оказывается, во многих случаях это эквивалентно заданию бесконечной цепочки функций распределения

Определение функций распределения. В последней строчке опечатка?

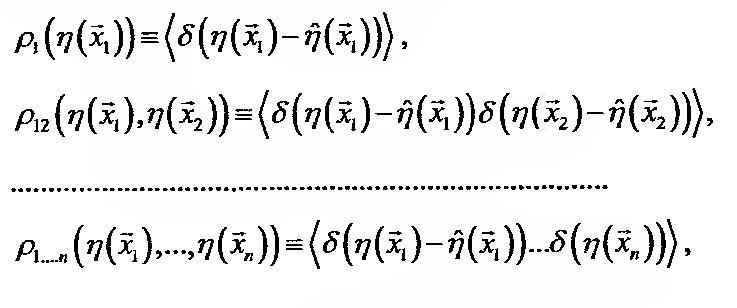
Угловатые скобки в этих формулах означают усреднение по пространству событий. В нашем случае, при конечном N это будет просто сумма вероятностей по каждой реализации. В общем случае это будет страшный функционал.

Что такое одночастичная функция распределения? Мы берем точку 0<x₁ <dN внутри нашей слоечки, и хотим узнать, какова вероятность там получить трещину? Мы уже сказали, что у нас это аксиома — эта вероятность равна t, но сейчас мы потренируемся на одноточечной функции распределения и с двухточечной будет понятнее. По определению, если мы знаем как измерять множества в пространстве событий разных слоистых структур, то нам надо взять множество всех слоек, у которых в точке x₁ трещина, а в остальных хоть трава не расти, и вычислить его меру

Оформление в стиле Питера Шольце. Ниже тоже самое записано формулами с исправлением описок.

$\rho_0(x)=\int\delta(0-\eta(x,\hat\omega))dP\hat\omega=t\sum\limits_{k=0}^{N-1}\frac{(N-1)!}{(N-1-k)!}t^k(1-t)^{N-k-1}=$ $t(t+1-t)^{N-1}=t$

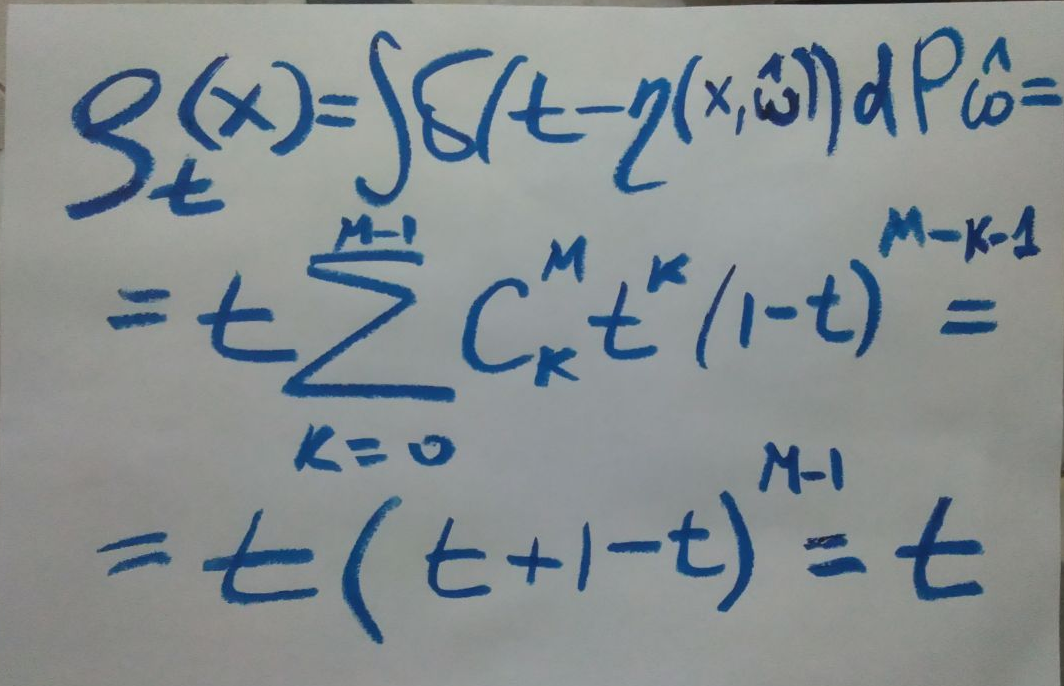
Что же на рисунке выше сделано? Дельта-функция под интегралом определяет, по какой области пространства надо интегрировать, а в данном случае суммировать. Нужно просуммировать вероятности всех двоичных последовательностей, в которых на фиксированной позиции расположен ноль. Поэтому один множитель t уже за знаком суммы, а суммируем мы по случаям, когда в среди оставшихся слоев нет трещин, есть 1 трещина, 2 трещины и т.д., до полностью треснутой слойки. Нужно учесть комбинаторику — сколькими способами могут распределиться трещины. Получается, буквально, бином Ньютона. И тавтологичный ответ — если вероятность трещины t, то вероятность трещины t.

Вот с двухточечной функцией распределения все будет интереснее! Запишем определение

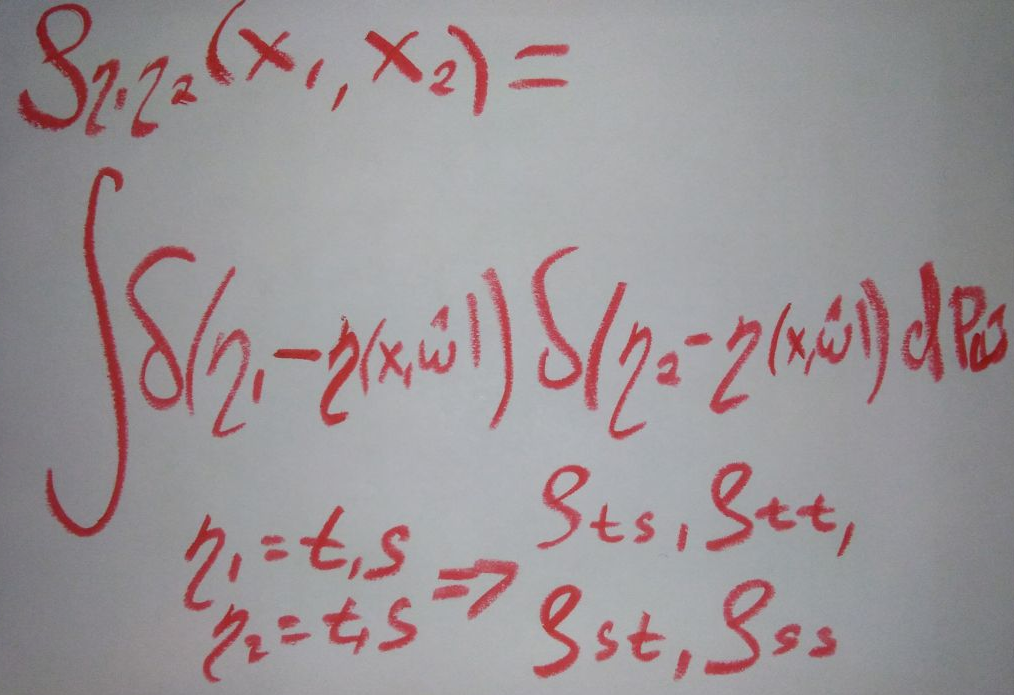
Во-первых, появилось 4 функции распределения: трещина-трещина, остов-трещина, трещина-остов, остов-остов. Во-вторых, точки x₂, x₁ могут либо попасть в разные слои (что точно произойдет, если x₂-x₁>d), либо они могут попасть в один слой. Зададим функцию, отмечающую попадание в разные слои П(x₁,x₂). Тогда за попадание в один слой будет отвечать функция U(x₁,x₂)=1—П(x₁,x₂). Вот так графически выглядят эти функции

П(x1,x2)=1 в области закрашенной голубым, U(x1,x2)=1 в неокрашенной области.

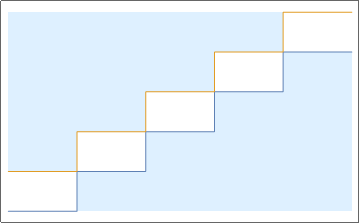
Давайте определимся — будем вычислять функцию распределения трещина-трещина. Тогда, если точки попали в разные слои, функция распределения будет равна

$t^2\Pi(x_1,x_2),$

а если в один слой, то

Множители t² и t точно также появляются в результате суммирования бинома Ньютона, как и для одночастичной функции распределения. Ниже приведу ответ для всех четырех функций распределения, а вам упражнение — вывести оставшиеся!

$\rho_{00}(x_1,x_2)=t^2\Pi(x_1,x_2)+tU(x_1,x_2),$ $\rho_{11}(x_1,x_2)=(1-t)^2\Pi(x_1,x_2)+(1-t)U(x_1,x_2),$ $\rho_{01}(x_1,x_2)=\rho_{10}(x_1,x_2)=t(1-t)\Pi(x_1,x_2).$

На картинке первая версия обозначений, еще не совсем удачная.

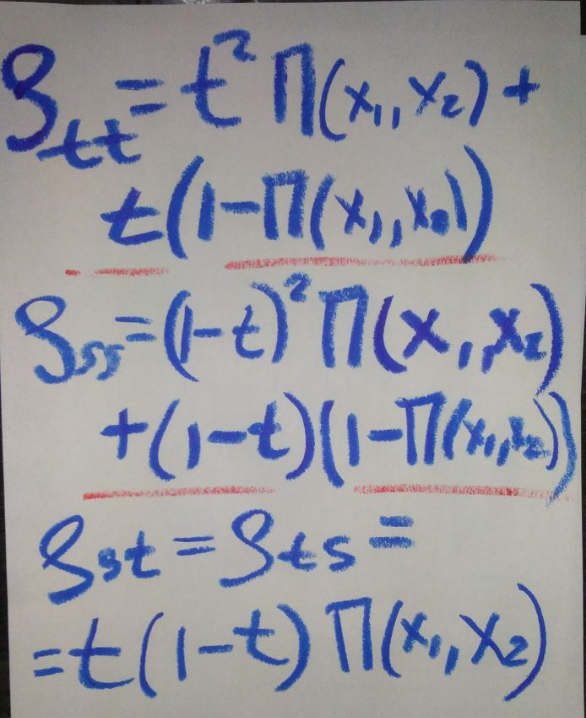
Ну, теперь этот процесс не остановить. Легко запишем трех-точечную функцию распределения трещина-трещина-трещина, при этом три точки должны попасть в трещины. Если все точки попали в разные слои , функция распределения будет равна

$t^3 \Pi(x_1,x_2)\Pi(x_2,x_3)\Pi(x_1,x_3).$

Если две точки попали в один слой, то функция распределения равна

$t^2\left(U(x_1,x_2)\Pi(x_1,x_3)\Pi(x_2,x_3)+permutaitons \right)$

И, наконец, если все три точки попали в один слой, то получим

Полная трехточечная функция распределения будет суммой этих трех слагаемых. Заметьте, в функциях распределения не фигурирует число слоев N. Поэтому, хотя в предельном переходе N->Infinity возникают трудности с определением меры в вероятностном пространстве, с функциями распределения все остается в порядке!

Теперь можно результаты наших трудов применить к осмыслению абстрактных свойств функций распределения.

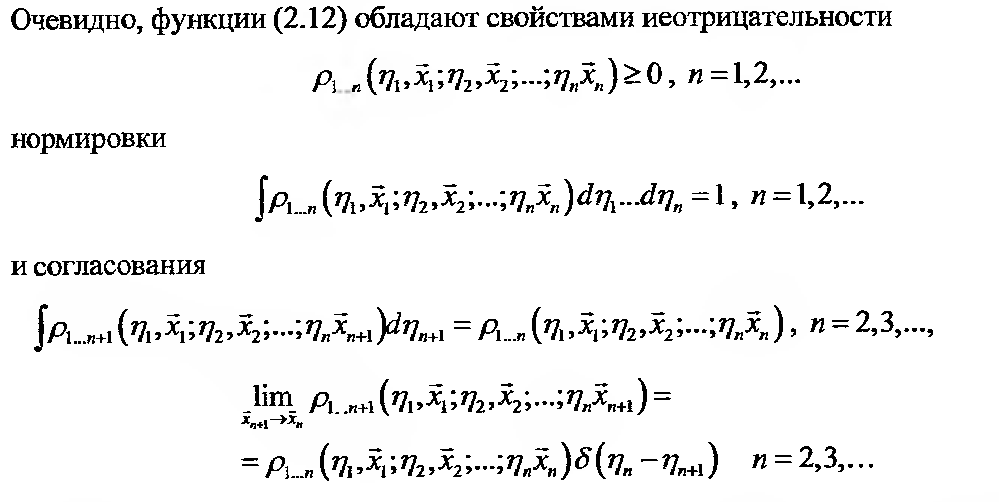
Проверяем по порядку. Неотрицательность имеется! Нормировка для одноточечной выполняется, потому что, сумма распределений для трещин и остова t+(1-t)=1. Для двух-точечной нужно сложить функции распределения трещина-трещина остов-остов и два раза трещина-остов

$\rho_{00}(x_1,x_2)+\rho_{01}(x_1,x_2)+\rho_{10}(x_1,x_2)+\rho_{11}(x_1,x_2)=1$

Если x₂,x₁ в разных слоях, эта сумма даст t²+(1-t)²+2t(1-t)=1. Если x₂,x₁ в одном слое, сумма получится t+1-t=1. Для двухточечной нормировка тоже имеется.

Согласование с пределом очевидно. Когда x₂=x₁ мы используем только слагаемые для попадания в одну клетку. Поэтому функции распределения трещина-остов равны нулю, а для совпадающих слоев — t*1 или (t-1)*1, то есть одночастичные распределения умноженные на дельта-символ,

$\rho_{00}(x_1,x_1)=t =t\delta(0-0),$

Согласование с интегралом — поскольку у нас 2 типа слоев, надо брать сумму, трещина-трещина и трещина-остов. Как ни странно, получится t

$\rho_{00}(x_1,x_2)+\rho_{01}(x_1,x_2)=t^2\Pi(x_1,x_2)+tU(x_1,x_2)+t(1-t)\Pi(x_1,x_2)=t(\Pi(x_1,x_2)+U(x_1,x_2))=t=$ $=\rho_0(x)$

И, наконец, у нас имеется свойство ослабления корреляций — если x₂-x₁>d, то двухчастичные распределения просто являются произведениями одночастичных распределения (t²=t*t и т.д.). Получается, что радиус корреляции — это толщина слоя. На этой радостной ноте, что черные и белые полосы в жизни не скоррелированы, мы сделаем паузу в исследование случайных слоистых структур.

Эпилог

В этом игрушечном примере можно проследить всю схему корректного математического описание случайных сред (полей), от меры в вероятностном пространстве до функций распределения. Можно пойти и дальше, и восстановить по этим функциям распределения исходную меру, но текст уже и так получился слишком большим. Дальше, можно деформировать наши функции распределения во что-то более реалистичное. Сгладить корреляции U(x₁,x₂), например, с помощью гауссианы (это будет соответствовать случайной толщине трещины). Добавить пространственных измерений и анизотропию. Можно сделать t зависящим от координаты, и т.д. Такие функции распределения появятся в итеративном вычислении среднего поля, который удобно изображать диаграммами. По мере погружения в эту тематику попробую зафиксировать результаты. В книжке есть невероятные разделы — про стрелу времени и квантовую механику Рязанова (никогда раньше о нем не слышал, но он Уиллера и Фейнмана переплюнул). to be continued…

ссылка на оригинал статьи https://habr.com/ru/articles/572018/

Ансамбль слоистых сред

Введение

От аксиом к примерам

Функции распределения

Эпилог

Комментарии

Добавить комментарий Отменить ответ