Гайд по мета-анализу результатов тестов

Привет! На связи команда аналитиков «Пятёрочки» X5 Tech.

Подсчитать и проанализировать можно не только A/B, но также подвергнуть анализу ряд тестов с общей нулевой гипотезой. Другими словами, протестировать результаты серии тестов с классическим статистическим выводом о значимости показателей этой серии, то есть провести мета-анализ.

На написание этой статьи меня вдохновило общение внутри моей классной команды, общение с одним из аналитиком Gett, а также данный пост и комментарии к нему по поводу статьи Ebay.

Считается, что мета-анализ стоит на ступеньку выше по доказательности, чем обычный тест, так как аккумулирует информацию по ряду тестов. Можно сказать, что он проводит операцию слияния данных (data fusion), давая оценку оценкам, поэтому и мета. И раз он сильнее по доказательности, то и позволяет увереннее внедрять статистически значимые инициативы. Про мета-анализ и поговорим в статье.

Мотивация к использованию

Допустим, в мобильном приложении «Пятерочка» решили протестировать новую структуру карточки товара. И в приложении «Перекрёстка» — ту же самую структуру, только со своим дизайном. Предположим также, что аудитории двух приложений не пересекаются.

У нас может быть несколько результатов, но рассмотрим два из них, первый – самый тривиальный и второй, который заставляет нас сомневаться:

Самый простой, когда оба значимы и эффект для нас положительный. Ладно бы был всего один тест, но когда оба показывают значимость в одну сторону, то таких два свидетельства ещё больше уверяют нас в том, что в инициативе по структуре карточки товара что-то есть. Такого рода мета-анализ осуществляется за доли секунды в наших головах.
Интересен другой случай: что если бы наши оба теста не прокрасились, но по абсолютной разнице указывали бы на то, что лучше новый дизайн, а p-value были бы у порога значимости? Вот тут мы и начинаем сомневаться. Проверить бы это.

Для второго случая, в частности, и подходит мета-анализ, когда у нас одна и та же общая нулевая гипотеза (допустим: «Наша фича XYZ не влияет…»).

Комментарий к размышлению

Вообще, тесты с общей H0 могут и должны вам напомнить случай повтора теста. У нас есть три сценария, когда это можно произойти:

Исследовательские группы не знают друг о друге, поэтому проводят тест одного и того же.
Репликация стат. значимого теста, чтобы ещё больше удостовериться в том, что эффект есть, но с соответствующей проблемой воспроизводимости.
Повтор теста в случае не стат. значимого результата, так как кто-то (например, из топ-менеджмента) слишком верит в свою гипотезу. Статистика показывает, что рано или поздно, когда эффекта на самом деле нет, повторение ложно прокрасится.

Мета-анализ как раз и служит агрегатором для набора результатов по всем трём пунктам.

Подводные камни

Но спешить сразу мета-анализировать свои тесты не стоит. Надо иметь ввиду несколько условий, чтобы сделать всё правильно:

Во-первых, тесты должны быть согласованы, когеренты. Иначе можно одинаковые по названию, но разные по смыслу и содержанию пилоты некорректно обобщить.

Во-вторых, надо максимально сохранять сравнимость групп из теста в тест. Если в одном тесте была раскатка фичи «XYZ», например, на пользователей Android, а на другом – на iOS, то это может давать гетерогенные (разные) эффекты, потому что поведение юзеров этих осей чаще всего разное. Тут есть разные выделенные сегменты, и будет некорректно проводить мета-анализ в таком случае. Чтобы вычленить эффект от тритмента, выборки должны быть рандомизированы для соблюдения влияния одних и тех же факторов не только на обе группы, но и между тестами.

В общем случае перед применением мета-анализа надо думать, например, cравнимы ли аудитории, чтобы не получилось, что вы сравниваете в тесте мягкое и пушистое.

Во-вторых, надо ответить на вопрос, участвуют ли люди из параллельного/предыдущего теста в другом тесте с той же H0. От этого зависит, с какой общей H0 вы имеете дело – с независимой или зависимой.

Общая H0: независимая и зависимая

Есть два случая обработки общей H0.

Независимая общая H0 – это когда у нас из теста в тест фичи идёт разная конфигурация юзеров/объектов в A/B.

В этом случае мы работаем с комбинацией статистик/p-value (и вероятностью таковую получить, если верна H0). Для этого случая мы рассмотрим метод Триппета, метод комбинированной вероятности Фишера (Fisher’s method, Fisher’s combined probability test) и метод weighted z-score (Stouffer’s, Liptak).

Зависимая общая H0 – это когда из теста в тест пользователи могут повторяться.

В случае зависимости – со связанными статистиками/p-value от одного и тоже набора объектов (юзеры, например) в A/B из теста в тест. Пример: последовательное (sequential) тестирование. В этом случае рассмотрим метод взвешенного гармонического среднего (weighted harmonic mean p-value).

Проверка независимой общей H0

Ещё раз рассмотрим возможные результаты двух тестов с общей гипотезой:

Оба теста стат. значимы. Зелёный прокрас, версия «B», оказалась лучше в обоих тестах. Тут не нужно применять никаких доп. тестов — всё говорит само за себя.
Оба теста не стат. значимы, p-value довольно большое. Тут тоже никаких дополнительных процедур не нужно.
Есть и другие комбинации, но самая интересная — следующая, когда оба теста не стат. значимые, но при этом в абсолютном выражении B лучше A в обоих случаях, а p-value на границе значимости: Действительно, пускай у нас второй тест покажет снова p-value = 0.051. В рамках двух независимых тестов с одной H0 мы не можем её отклонить, однако сама комбинация [0.051, 0.051] кажется уж больно маловероятной. Мы это видим и нас могут терзать сомнения, так уж ли мы не можем отклонить H0, если рассмотрим оба этих p-value вместе?

Метод Типпета (Tippets method)

Это метод-пионер, 1931 год. Логика простая: берём из набора p-value самое минимальное, получаем статистику T:

$T=min(p_{i})$

Подставляем в формулу, которая, будьтам вместо «T» параметр «альфа», относит нас FWER, ошибки первого рода хотя бы один раз в серии тестов:

$1-(1-T)^{k}$

где k — кол-во p-value

Если результат меньше заданной альфы, тогда стат. значимо.

Простота метода сравнится лишь с его консервативностью, что неудивительно, так как если у нас k тестов, то минимальная p-value для значимости должна быть не более alpha/k, что является поправкой Бонферрони – самой известной и самой жёсткой для контроля FWER.

Например, p-values = [0.1, 0.025] при альфа = 0.05. Минимум = 0.025 (что по случайности равно alpha/k).

$1-(1-0.025)^{2}\sim 0.049..$

А вот минимум = 0.026 показал бы другое значение, не стат. значимое.

Скрытый текст

Раз есть минимум из набора p-value, то есть и максимум.

$S=max_{}(p_{i})$

Выбрав максимум, мы можем провести один из двух тестов:

1.1. Статистика Friston’a:

1.2. Статистика Nichols:

S – тут просто смотрим, значимо ли само значение максимальной p-value

В литературе встречается и статистика Edgington’a (1972 год), которая представляет собой просто сумму p-value:

$\sum_{i=1}^{k}p_{k}$

Но она совсем не рекомендована к использованию в силу того, что если в комбинации p-value присутствует одна большая p-value (например, 0.6), то какими бы маленькими не были бы прочие, = 0.0002, гипотеза никогда не будет отвергнута (Hedges, Olkin, 1985 г., “Statistical Methods for Meta-Analysis”)

Метод Фишера (Fisher’s method, Fisher’s combined probability test)

Для оценки комбинации предложил свой метод сэр Рональд Фишер в 1934 году. Давайте к нему “подведёмся”.

Мы знаем, что когда верна H0, теоретическое p-value имеет вид равномерного распределения:

Пускай мы провели 2 теста подряд, когда верна H0, получив следующую комбинацию p-values = [0.05, 0.9]. Проведём ещё два теста подряд (когда верна H0), получим новую комбинацию = [0.6, 0.7]. Отразим на графике, где первое p-value по оси X от первого теста, а второе по оси Y – от второго:

Где 2 комбинации, там и 100500 комбинаций:

Получаем равномерно заполненный квадрат.

Вернёмся к комбинации = [0.05, 0.9]. Какие комбинации можно получить с такой же или меньшей вероятностью?

Ответ: такие комбинации, которые при перемножении p-value’s будут равны или меньше, чем 0.05*0.9 = 0.045. Почему перемножение? Да как раз потому, что у нас два независимых события со своими вероятностями, и мы смотрим совместное их появление. Всё по классической теории вероятности.

Итак, что ещё даст значение, равное или меньше, чем 0.045? Например, конечно, точка [0.9, 0.05] (выделана красным):

Далее рассмотрим вероятность взять из нашего равномерного распределения p-value от 0 до 1 такое p-value, чтобы оно было меньше или равно 0.05.

Формальная, P(0 <= p-value <= 0.05):

Например, если будем уменьшать только первое p-value: 0.04*0.9
Если будем уменьшать только второе p-value: 0.05*0.89
Если будем уменьшать оба p-value: 0.04*0.89
Если будем первое p-value увеличивать, а второе p-value уменьшать (до некоторого предела, конечно): 0.18*0.25

Тогда все точки (комбинации), которые удовлетворяют этим условиям на нашем графике 100 500 комбинаций будут следующими, выделены красным:

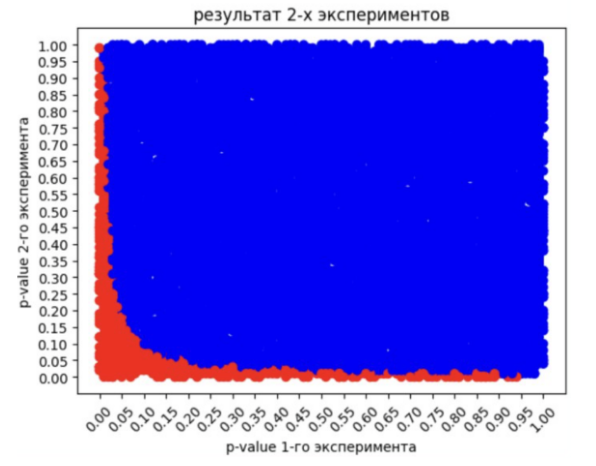
Далее нам нужно рассчитать долю красных точек против всех точек (и красных, и синих):

$p_{[0.05, 0.9]}=\frac{\color{red}{red}}{\color{red}{red}+\color{blue}{blue}}\simeq 0.18$

Это и есть p-value нашего с вами мета-анализа комбинации [0.05, 0.9].

Скрытый текст

Для любознательных: площадь, покрытую красными точками, в данном двумерном случае можно подсчитать и классическим способом — аналитически. Так как её граница задаётся уравнением p1*p2 = 0.045:

$0.045 + \int_{0.045}^{1} \frac{0.045}{p_1} dp_1 \approx 0.185$

Вернёмся к случаю с [0.051, 0.051]. Вот наш результат, мета-pvalue в картинке:

P[0.051, 0.051] = 0.018, то есть стат. значимый результат! Интерпретация такого “мета p-value” следующая – вероятность получить такую вероятность совместных событий (p-value) при условии верности общей H0.

На картинке выше видно, какую долю от H0 составляет такая комбинация: действительно, очень небольшую! Что бьётся с нашей интуицией о малой вероятности случайности такого исхода.

На википедии есть очень выразительная картинка для комбинации из двух p-value:

Но не всё так просто, к сожалению. Дело в том, что таким подходом можно пользоваться лишь при незначительном объёме экспериментов. Если количество экспериментов будет расти, то:

При расчёте методом Монте-Карло нам понадобится много ресурсов на генерацию множества вариантов.
При аналитическом расчёте также понадобится много вычислительных ресурсов, так как интегралы будут многомерными.

Поэтому весьма кстати был бы такой универсальный расчёт, который было бы просто реализовать. Что и предложил Фишер.

Вывод статистики метода Фишера

Основная проблема в том, что комбинация p-value, когда верна общая H0 (global H0):

$\prod_{i=1}^{n}p_{i}$

не распределяется равномерно, а также не сводится ни к какому известному распределению, и явно будет меняться от количества p-value, которые участвую в комбинации. Плохая история во время расчётных таблиц значимости и пр.

Поэтому нам нужно такое распределение, к которому будет сводиться значение нашей комбинации, когда эффекта нет. Распределение, которое будет зависеть только от количества совместных вероятностей. И таким распределением оказался Хи-Квадрат.

Вот что сам Фишер говорит весьма кратко в конце главы про тест Хи-Квадрат для goodness-in-fit (адекватность модели) про свой метод [Fisher, 1934. Statistical Methods for Research Workers, 5th Edition, стр. 103, Глава IV, 21.1]:

When a number of quite independent tests of significance have been made, it sometimes happens that although few or none can be claimed individually as significant, yet the aggregate gives an impression that the probabilities are on the whole lower than would often have been obtained by chance. It is sometimes desired, taking account only of these probabilities, and not of the detailed composition of the data from which they are derived, which may be of very different kinds, to obtain a single test of the significance of the aggregate, based on the product of the probabilities individually observed.

The circumstance that the sum of a number of values of ꭓ² is itself distributed in the ꭓ² distribution with the appropriate number of degrees of freedom, may be made the basis of such a test. For in the particular case when n=2, the natural logarithm of the probability is equal to ½ꭓ². If therefore we take the natural logarithm of a probability, change its sign and double it, we have the equivalent value of ꭓ² for 2 degrees of freedom. Any number of such values may be added together, to give a composite test, using the Table of ꭓ² to examine the significance of the result.

Распределение Хи-Квадрат, согласно определению, это:

$\chi^2_{k}\sim \sum_{i=1}^{k}Z^2_{i}$

где Z_i – стандартизированные случайные величины, распределённые согласно нормальному распределению. Cумма Хи-Квадратов, как отмечает Фишер, тем и примечательна, что даёт также Хи-Квадрат:

$\chi^2_{k_{1}}+\chi^2_{k_{2}}= \sum_{i=1}^{k_{1}}Z^2_{i}+ \sum_{i=1}^{k_{2}}Z^2_{i}=\sum_{i=1}^{k_{1}+k_{2}}Z^2_{i}=\chi^2_{k_{1}+k_{2}}$

Мы знаем, что у распределений есть их кумулятивная функция F(x), которая определена от 0 до 1, прямо как p-value.

Пример для разных нормальных распределений. — Пример для разных *нормальных* распределений.

И что если нам каждому p-value отдавать результат, обратный кумулятивной функции для, например, распределения Хи-Квадрат, смотря на чудесное свойство суммирования в п.1?
Оказывается, мы вполне можем это сделать, применив метод обратного преобразования Смирнова, согласно которому «изнепрерывного равномерного распределения можно получить выборку из распределения, задаваемого функцией распределения». Это выглядит так:

То есть мы передаём значение U в обратную функцию для F(x), получаем значение «x».

Пусть у нас есть случайная величина, распределённая равномерно:

$\eta\sim U_{0,1}$

И есть функция F — произвольная функция распределения. Тогда другая случайная величина:

$\xi=F^{-1}(\eta)$

имеет функцию распределения F.

Рассмотрим функцию распределения Хи‑Квадрат, где k — степень свободы, а Г — гамма-функция

$F(x, k)= \int_{0}^{x}\frac{t^{\frac{k}{2}-1}e^{-\frac{t}{2}}}{2^{\frac{k}{2}}\Gamma(\frac{k}{2})}dt$

Выглядит страшненько, однако визуально это выглядит куда безобиднее:

В общем виде искать обратную функцию будет сложно, но нам и не нужно, поэтому рассмотрим, как она будет выглядеть для степени свободы k=2, использовав свойство гамма-распределения Γ(1) = 0! = 1

$F(x, 2)= \int_{0}^{x}\frac{t^{\frac{2}{2}-1}e^{-\frac{2}{2}}}{2^{\frac{2}{2}}*1}dt=\int_{0}^{x}\frac{e^{-\frac{t}{2}}}{2}dt=1-e^{-\frac{x}{2}}$

Получилась весьма простая функция, которая соответствует функции экспоненциального распределения с параметром λ=½, но самое важное — другое: от такой функции достаточно просто найти обратную функцию!

$F_{\chi^2}(x, 2)=1-e^{-\frac{x}{2}}$

x тут у нас — это значение статистики Хи-квадрат.

Так как F(x) распределена от 0 до 1, то заменим F(x) на p.

$p=1-e^{-\frac{1}{2}x}$

Немного переписав, мы получим следующее:

$e^{-\frac{1}{2}x}=1-p$

Так как у нас p распределяется от 0 до 1, то и 1-p так же. Вот предельные случаи:

1 — 0 = 1

1 — 1 = 0

значит,

$e^{\frac{1}{2}x}=p$

Далее нам нужно выразить x, что несложно, если взять натуральный логарифм и провести простые алгебраические операции:

Таким образом, согласно теореме, если мы хотим получить из случайной величины из равномерного распределения:

$\eta\sim U_{0,1}$

случайную величину с функцией распределения

$\xi\sim \chi^2_{k=2}$

то мы должны совершить преобразование

$\xi\sim -2ln(p)$

Так какх — это статистика Хи-квадрат, то, как мы выяснили выше (п. 1), их сумма тоже даёт Хи-Квадрат. Значит, если у нас k таких х, то в общем случае, при верности общей нулевой гипотезы (все p-value распределены равномерно), формула такая:

$X=-2\sum_{i=1}^{k}ln(p_{i})$

Что как раз решает нашу изначальную проблему произведения двух p-value и сводит его, произведение, в преобразованном виде к статистике X, которая распределяется как:

$\chi^2_{2k}$

Учёт разного объёма выборок

Для учёта разного объёма выборок в независимых тестах как будто хорошая идея — это ввести веса, например, согласно такому правилу (Если размеры выборки будут совпадать, то веса при всех p-value будут равны 1, что вернет нас к базовой формуле):

$X=-2\sum_{i=1}^{k}w_{i}ln(p_{i}), \space \space w_{i}=\frac{max_{k}([n_{1},..,n_{k}]}{n_{i}}$

Важно: в случае весов статистика не будет распределяться согласно Хи‑Квадрату, требуются разные вычисления статистики и p‑value, если веса повторяются и если они уникальные. Как именно вычислять, см. Thiagarajan, «Using weights p‑values in Fisher»s Method». Для учёта весов есть другой метод, более конкретный — weighted z‑score.

Наглядные преобразования

Проведём последовательно ряд преобразований с равномерным распределением p-value:

Преобразуем это распределение через умножение на (-1) и натуральный логарифм от конкретного p-value:

Наш результат преобразования — это экспоненциальное распределение:

Теперь умножим значение из этого экспоненциального распределения на 2. И мы получим Хи-Квадрат (Сhi-Squared) c параметром k=2:

Убедимся, что совпадает с Хи-Квадрат: сгенерируем выборку по соответствующему закону и наложим на полученное выше распределение.

Идеально!

Стоит также напомнить, как выглядит зависимость распределения Хи-Квадрат от k=n-1, указатель количества сторон (монетка: 2 стороны, k=1; кубик: 6 сторон, k=5):

Ведь где есть одна серия тестов, когда верна H0, которая даёт равномерное p-value, там может быть и вторая! Преобразуем и это второе равномерное распределение. Так как мы делаем то же самое, то нет ничего удивительного в том, что у нас получается такое же Хи-Квадрат распределение (справа):

Теперь просто сложим, то есть просуммируем:

Результат суммы будет следующий — Хи-Квадрат (k=4):

$stats=-2\sum_{i=1}^{k}ln(p_{i})$

Обратите внимание, что в формулу добавился просто знак суммы.

Видно, что суммарный Хи-Квадрат зависит от k. Чтобы понять, какой он будет, мы должны 2 умножить на k, где k — количество тестов. Получим 2k. Отсюда и общий случай, который мы вывели ранее:

$\chi^2=-2\sum_{i=1}^{k}ln(p_{i})$

То есть имея набор из k p‑value, мы их сначала преобразовываем, потом суммируем (от 1 до k), получая значение статистики. Эта статистика «приземляется» на Хи-Квадрат распределение с параметром 2k с заданными границами значимости. Далее смотрим, стат. значим или нет наш результат. Например, у нас было два независимых теста:

p-value, очевидно, тоже меньше 0.05, если мы его подсчитаем

Небольшой подводный камень метода Фишера

Он оперирует только p-value без привязки к значению статистики, точнее, если позволите, к абсолютной разнице между А и B.

У этого есть последствия. Например, в одном случае B был стат. значимо лучше, в другом хуже. Я не исключаю такой возможности и при этом гарантирую, что ваша мета-p-value будет стат. значимой.

Но как это интерпретировать? Это вопрос. Точно не в пользу или в противовес B.

Ваши возможные действия:

Не проводить мета-анализ.
Использовать более подходящий метод, который не оперирует исключительно p-value: это точно убирает риск не обратить внимание на разность в знаках/прокрасах стат. значимых результатов. Лучше применить weighted z-тест, который как раз учитывает а) статистику б) размер выборок в каждом из тестов.

Метод Пирсона (Pearson’s Method)

Если вернуться к выводу (5) метода Фишера:

$e^{-\frac{1}{2}x}=1-p$

То мы можем не делать замену на просто p, а сразу вывести X:

$X=-2\sum_{i=1}^{k}ln(1-p_{i})$

Сторого говоря, Пирсон предложил свой метод раньше, чем Фишер (1933 год). Почему тогда более известен Фишер?

Возможно, ответ такой: при одной и той же комбинации у нас получится разное значение статистики. Например, [0.051, 0.051] даст следующее:

Fisher: 11.9
Pearson: 0.209

Так как Хи-квадрат считается односторонним тестом,

Скрытый текст

что спорно: если наша статистика в тесте goodness-of-fit очень маленькая, то у нас может возникнуть оправданное впечатление, что наши данные слишком уж согласуются с моделью. Подозрительно. Самый известный случай это анализ данных Менделя, который сделал Фишер, где данные уж больно хорошо согласовывались с ожиданиями. См. Mendelian_paradox

то “мета p-value” по Пирсону должно быть близко к одной единице, однако тест вам выдаст 0.0051. Дело в том, что критическая область (скажем, 0.05) находится слева для данного метода. Вот и вся разница.

Полагаю, что к 1930-м годам (да как и сейчас) табличные значения по Хи-квадрату были в подавляющем большинстве источников для правой стороны. Потому-то Фишер сейчас куда больше на слуху.

Важно отметить, что результат по методу Пирсона в общем случае не будет совпадать с Фишером. В силу того, что Хи-Квадрат ассиметричен, то Пирсон чувствителен к большим p-value (изменением одного из p-value в большую сторону) в комбинации, а Фишер – к малым (изменением одного из p-value в меньшую сторону).

Метод Mudholkar–George

Зачем метаться между Фишером и Пирсоном, если можно взять некоторое их среднее? Своё решение предложили Mudholkar и George в виде логита:

$\sum_{i=1}^{k}ln(\frac{p_{i}}{1-p_{i}})$

Статистика имеет распределение, описываемое k-fold свёрткой (k-fold convolution) F_k(*)

Скрытый текст

Для снижения уровня абстракции и примерного понимания, о чем речь, рекомендую великолепное видео по свертке случайной величины от 3Blue1Brown

обратной функции от логита:

$F(x)=\frac{1}{1-e^{-x}}$

Weighted Z-score (Shouffer’s)

Иной подход предложил социолог Shouffer (и другие: Liptak, Zezhong, Zaykin): через оперирование статистикой теста как есть.

Сначала рассмотрим one-sample z-test. Значение нашей статистики будет где-то тут:

Наша нулевая гипотеза (H0) в том, что выборка принадлежит генеральной с некой Mu. При этом если выборка действительно из этой генеральной, то логично заключить, что ожидаемая разница между выборочной средней и Mu должна быть равна нулю.

Стандартизированные разницы выборочных средних больших выборок имеют z-нормальное распределение, где ожидаемый ноль будет равен z_score = 0. То есть формула стандартизации всех значений распределения разниц выборочных средних и Mu выглядит на самом деле так (Mu = 0):

$\frac{\bar{x}-0}{\frac{\sigma_{x}}{\sqrt{n}}}=\frac{\bar{x}}{\frac{\sigma_{x}}{\sqrt{n}}}$

Наш следующий шаг — допустить, что мы взяли, условно, бесконечно большую выборку из нашей генеральной, подсчитали её среднее и стали стандартизировать. Наше среднее в числителе — это среднее этой бесконечно большой выборки.

Далее у нас начнётся простая дотошная алгебра и замены переменных. Рекомендую тут налить чашечку чая/кофе, а потом следить за руками:
Вынесем корень из n в числитель, согласно правилу дробей:

$\sqrt{n}\frac{\bar{x}}{\sigma_{x}}=\frac{\sqrt{n}\frac{\sum_{}^{}X}{n}}{\sigma_{x}}=\frac{\sqrt{n}\frac{\sum_{}^{}X}{\sqrt{n}\sqrt{n}}}{\sigma_{x}}=\frac{\frac{\sum_{}^{}X}{\sqrt{n}}}{\sigma_{x}}=\frac{\sum_{}^{}X}{\sqrt{n}\sigma_{x}}$

А что если РАЗБИТЬ нашу бесконечно большую выборку на две – S1 и S2? А давайте

$\frac{\sum_{}^{}S_{1}+\sum_{}^{}S_{2}}{\sqrt{n}\sigma_{x}}$

Дальше перепишем суммы через опять же определение среднего:

$\bar{s}=\frac{\sum_{S}^{}}{n_{s}}$ $\sum_{}^{}S=n_{s}\bar{s}$

Поставляем в 3:

$\frac{n_{s_{1}}\bar{s_{1}}+n_{s_{2}}\bar{s_{2}}}{\sqrt{n}\sigma_{x}}$

Логично, что n в числителе – это у нас n_{s1} + n_{s2}:

$\frac{n_{s_{1}}\bar{s_{1}}+n_{s_{2}}\bar{s_{2}}}{\sqrt{n_{1}+n_{2}}\sigma_{x}}$

Вынесем сигму:

$\frac{\frac{n_{s_{1}}\bar{s_{1}}}{\sigma_{x}}+\frac{n_{s_{2}}\bar{s_{2}}}{\sigma_{x}}}{\sqrt{n_{1}+n_{2}}}$

Далее снова n заменим на умножение корней:

$\frac{\frac{\sqrt{n_{s_{1}}}\sqrt{n_{s_{1}}}\bar{s_{1}}}{\sigma_{x}}+\frac{\sqrt{n_{s_{2}}}\sqrt{n_{s_{2}}}\bar{s_{2}}}{\sigma_{x}}}{\sqrt{n_{1}+n_{2}}}$

Пускай корень из n – это у нас w, вес:

$w=\sqrt{n}$ $\frac{w_{1}\frac{\sqrt{n_{s_{1}}}\bar{s_{1}}}{\sigma_{x}}+w_{2}\frac{\sqrt{n_{s_{2}}}\bar{s_{2}}}{\sigma_{x}}}{\sqrt{w^2_{1}+w^2_{2}}}$

Так как у нас была изначально бесконечно большая выборка, а мы поделили её на две части, то они, по сути, тоже бесконечны. Ну или важнее другое — они также очень большие. Известно, что дисперсия больших выборок крайне близка к дисперсии генеральной, и вообще — к дисперсии друг друга:

$\sigma_{s_{1}},\sigma_{s_{2}}\sim \sigma_{x}$ $\frac{w_{1}\frac{\sqrt{n_{s_{1}}}\bar{s_{1}}}{\sigma_{s_{1}}}+w_{2}\frac{\sqrt{n_{s_{2}}}\bar{s_{2}}}{\sigma_{s_{2}}}}{\sqrt{w^2_{1}+w^2_{2}}}$

Заметим, что в числителе у нас около весов, по сути, те же стандартизации выборочных средних, то есть z-значения:

$\frac{w_{1}\frac{\color{red}{\sqrt{n_{s_{1}}}\bar{s_{1}}}}{\color{red}{\sigma_{s_{1}}}}+w_{2}\frac{\color{red}{\sqrt{n_{s_{2}}}\bar{s_{2}}}}{\color{red}{\sigma_{s_{2}}}}}{\sqrt{w^2_{1}+w^2_{2}}}$

Тогда:

$Z_{combined}\simeq \frac{w_{1}Z_{1}+w_{2}Z_{2}}{\sqrt{w^2_{1}+w^2_{2}}}$

В общем виде для k-тестов формула следующая:

$Z\simeq \frac{\sum_{i=1}^{k}w_{i}Z_{i}}{\sqrt{\sum_{i=1}^{k}w_{i}^2}}$

Готово!

Рассмотрим пример на базе one-sample теста. Пускай мы собрали сначала одну выборку и протестировали некое Mu, а потом собрали вторую выборку из той же совокупности и протестировали то же Mu. Получили вот такие результаты:

Пускай у нас границы значимости [-1.96, 1.96]

$\frac{w_{1}Z_{1}+w_{2}Z_{2}}{\sqrt{w^2_{1}+w^2_{2}}}=\frac{141.42*2.4+83.66*(-0.5)}{\sqrt{20000+7000}}=\frac{297.578}{164.3167}=1.811$

Результат не стат. значимый, но давайте и это, в том числе, увидим:

Осталось переложить это на классический two-sample t-test:

$Z_{combined}\simeq \frac{w_{1}Z_{1}+w_{2}Z_{2}}{\sqrt{w^2_{1}+w^2_{2}}}=\frac{w_{1}\color{red}{\frac{A_{1}-B_{1}}{\sqrt{\frac{\sigma_{a_{1}}}{n_{a_{1}}}+\frac{\sigma_{b_{1}}}{n_{b_{1}}}}}}+w_{2}\color{red}{\frac{A_{2}-B_{2}}{\sqrt{\frac{\sigma_{a_{2}}}{n_{a_{2}}}+\frac{\sigma_{b_{2}}}{n_{b_{2}}}}}}}{\sqrt{w^2_{1}+w^2_{2}}}$

В красным выделена формула two-sample t-test.

Круто? Да вообще!

Несложно вывести и доверительный интервал прямо из этой формулы, если добавить к этому Mu_эффекта. Но так как тестов для мета-анализа может быть больше двух(скажем, n), то для этого тот же автор из Ebay предлагает следующий алгоритм для подсчётов интервала, а заодно и подсчитать комбинированную абсолютную разницу:

Для начала использовать нормализацию весов, которая в сумме даёт единицу:

$\phi_{1}=\frac{w_{1}^2}{\sum_{i=1}^{n}w_{i}^2}, \space \space \sum_{i=1}^{n}\phi_{i}=1$

Важно: вес для каждого A/B теста рассчитывается от общего размера выборок во всех тестах. И «пхи» будет одна на каждый A/B.

Приведу dummy-пример:

Тогда нормализованный вес первого теста будет такой (напомню, что вес теста равен корню из объёма обеих групп теста):

$\phi_{1}=\frac{w_{1}^2}{\sum_{i=1}^{n}w_{i}^2}=\frac{(\sqrt{6})^2}{(\sqrt{6})^2+(\sqrt{10})^2}=\frac{6}{16}=0.375$

По аналогии считаем второй вес:

$\phi_{2}=\frac{10}{16}=0.625$

2. Считаем комбинированные средние для A и B:

$\mu_{A_{combined}}=\sum_{i=1}^{n}\phi_{i}\mu_{i_{A}}, \space \space\mu_{B_{combined}}=\sum_{i=1}^{n}\phi_{i}\mu_{i_{B}}$

где Mu_i – средний по выборкам по каждой из сторон контроль-тест независимых тестов. В сущности, это просто weighted averages по А и по B, которые учитывают различия в количестве аудитории.

Подсчитаем сначала выборочные средние:

После уже взвешенные, сначала для A:

$\mu_{A_{combined}}=\sum_{i=1}^{n}\phi_{i}\mu_{i_{A}}=0.375*2+0.625*4=3.25$

Потом по аналогии для B:

$\mu_{B_{combined}}=7.125$

3. Далее вычисляем дельту:

$\Delta_{comb}=\mu_{A_{combined}}+\mu_{B_{combined}}$

Отсюда и далее уже не вижу смысла продолжать расчет примера, там всё идёт как по рельсам. Осталось немного:

Дисперсия для эффекта. У нас будет она записываться через SE (Standard Error) Напомню, что это знаменатель в two-sample t-test’e:

$SE=\sqrt{(\frac{\sigma_{a}}{\sqrt{n_{a}}})^2+(\frac{\sigma_{b}}{\sqrt{n_{b}}})^2}$

Комбинированная дисперсия считается так:

$SE^2_{comb}=\sum_{i=1}^{n}\phi^2_{i}SE^2_{i}$

Формулы не пугаемся: дисперсия эффекта тоже зависима от размера аудитории этого теста. Поэтому это, по сути, weighted variance. И неудивительно, что она похожа на формулу подсчёта weighted average.

Там где дисперсия, там и стандартная ошибка:

$SE_{comb}=\sqrt{\sum_{i=1}^{n}\phi^2_{i}SE^2_{i}}$

Итого, у нас всё есть. И выходим на классический интервал для эффекта в совокупности:

$\mu_{comb}\pm Z_{comb}SE_{comb}$

Готово!

Вот такой вот метод, который при этом тесно связан с самым, пожалуй, первым в рамках статистики методом тестирования — z‑тестом.

Почему, возможно, он больше подходит, чем Фишер

У него, на мой взгляд, есть ряд преимуществ перед методом Фишера:

Более привычная и интерпретируемая для нас статистика: z‑статистика, тем более, что сравнение средних — это самый часто встречающийся случай.
У этой статистики есть знак, который показывает направление эффекта.
Также можно визуализировать и визуализация а) куда понятнее, чем в методе Фишера б) представима и неизменчива, если тестов n‑штук.
Уточняет эффекты через доверительные интервалы в абсолютных значениях.
Автор статьи Whitlock «Combining probability from independent tests: the weighted Z‑method is superior to Fisher’s approach» доказывал на серии симуляций, что данный критерий мощнее метода Фишера. Правда, он подчёркивал, что а) именно weighted версия б) при одинаковых весах результаты идентичны Фишеру в) нет ни слова о природе данных, что как раз учитывали другие авторы (Heard, Rubin‑Delanchy — будут далее), анализируя функции оценки комбинации данных.

Есть и недостаток: для прочих стат. критериев нужно идти через p-value. Для других стат. критериев логичнее использовать метод Фишера.

Обзор H0 c критическими областями для комбинации из двух p-value для методов, которые на слуху, с альфой = 0.05

Красная зона – это критическая область с альфой = 0.05, синия – зона не стат. значимого результата

Что выбрать-то?

Это, при соблюдении всех допущений, вопрос прежде всего мощности критерия. Статья Heard и Rubin-Delanchy «Choosing Between Methods of Combining p‑values» (2017 год) даёт следующий краткий итог:

Метод Edgington’a обсуждается под катом в конце параграфа про метод Типпета

Важно:

1) Авторы пишут конкретно, что «Table 1 proposes an informal rule‑of‑thumb for choosing a p‑value combination method, based on the underlying data types and tests that gave rise to the p‑values».

Если очень просто, то это неформальное правило, поэтому помните, что нужно поразмышлять над наблюдениями, прежде чем сделать fit → result. Классика.

2) “The theory … gives the optimal methods for combining p‑values in some particularly tractable cases. By the continuity of the p‑value combination methods considered, it follows that the same methods will be near‑optimal for distributions which are similar to these tractable cases.”

Методы будут достаточно оптимальны и для тех распределений, что близки к указанным в таблице.

3) Спорна приведённая тут статистика Edgington’a (под спойлерами в методе Типпета подсветили её недостаток).

Проверка зависимой общей H0

Данная глава будет скромнее, но и случай зависимости тестов с одной стороны вполне обычный, а с другой — в контексте мета‑анализа исследований достаточно редкий.

Обычный вот в каких сценариях:

1.1. Проверка однородности подобранных групп через множество тестов по соц.дему и метрикам. Все тесты будут зависимы от одной и той же конфигурации выборок.

1.2. При проверке множества метрик после применения поправок мы можем обнаружить, что некоторые положительно прокрашены. Мы можем сделать заключение, что вот в этим метриках B лучше A. Неплохо, что B лучше в этих метриках, но что если для заказчика этого недостаточно, чтобы начать раскатку, скажем, по экономическим причинам? Тут могла бы помочь в качестве доп. оценки «мета p‑value» всех результатов. Только стоит держать в голове общую H0, которая будет про однородность в средних, а не среднего по какому-то показателю, как это могло бы быть в ряде разных исследований.

Достаточно редко это про случаи исследований, где зависимость может возникнуть, когда из теста в тест в рамках одной и той же гипотезы пользователи могут повторяться. Речь, в том числе, и о частичном попадании участников прошлого теста в новый. Поэтому p-value таких тестов зависимы от одних и тех же пользователей.

Повтор теста это, в целом, проблема, так как тот, кто ждёт прокраса, обязательного его дождётся. Поди потом объясни бизнесу, что это, скорее всего, случайность. Мало того, надо ещё убедиться, что не будет перетока предыдущего контроля в тестовую группу, а из тестовой — в контроль на каждом следующем тесте.

Но допустим, у нас был один тест, он не прокрасился, далее тест повторился, перетока в контроль не было, но пользовали прошлой тестовой группы попали частично или полностью в новую тестовую группу, которая кратно меньше (как и контроль) предыдущего теста, но при этом результат значимый:

Первый тест не стат. значимый, а второй стат. значимый. Как быть? В случае зависимых данных частый ход — это усреднить данные: (0.03+0.07)/2 = 0.05. В целом, cтат. значимо, получается? Но:

Мы знаем, что у нас повтор теста (так сказать, дождались прокраса).
Как же быть с тем, что у нас разный размер аудитории по каждому из тестов?

На помощь приходит harmonic mean p-value:

$H(p1, p2, ...)=\frac{\sum_{i=1}^{n}w_{i}}{\sum_{i=1}^{n}\frac{w_{i}}{p_{i}}}$

w_i – это нормализованный вес p-value, зависящий от общего размера выборок каждого теста (сумма нормализованных весов = 1).

Harmonic Mean P-value (HMP)

Вывод метода

Как и в других методах, интересно проследить, почему, собственно, взвешенное гармоническое среднее? К сожалению, это будет чуть посложнее, чем всё предыдущее, так как мы сделаем шаг из привычного нам «фреквенсистиского» [частотного] подхода в статистике к редкому «лайклихудистскому» [likelihoodist]. Но постараемся не уходить в детали, а выделить главные вехи вывода.

Метод в 2019 году предложил Daniel Wilson, он начал со сравнения двух правдоподобий (likelihood).

$(1) \space R=\frac{P(Data=x|\theta=M_{A})}{P(Data=x|\theta=M_{0})}$

Скрытый текст

Пример:

Представьте, что вы подобрали котика на улице ростом 20 см. У вас может возникнуть ряд гипотез о том, из какой популяции вам подобралось такое счастье. Допустим, одна популяция с Mu_0 = 24, а другая с Mu_A = 25.

Тогда:

$P(Data=20|\theta=25) \sim0.025$ $P(Data=20|\theta=24) \sim0.01$

Визуально это могло бы выглядеть так:

Вероятность в кавычках потому, что мы имеем дело с непрерывной величиной и по-хорошему по всей строгости должны были считать вероятность в рамках диапазона.

Почему Wilson начал с такого теста? Стоит сказать, что такое отношение — это отправная точка в последовательном тестировании (Sequential Testing), что является попыткой ускорить через раннюю остановку идущий A/B без проблемы подглядывания. Это значит, что такой метод контролирует FWER (ошибку 1-го рода хотя бы 1 раз на всю серию тестов), актуальную для множественного тестирования (последовательное тестирование как раз вариант множественного)

Логично, что для последовательного тестирования (получившие нынче вторую жизнь старые-добрые SPRT и mSPRT алгоритмы) в каждом тесте правдоподобий мы используем всю полноту имеющейся информации нашего A/B на данный момент. Значит, наши статистики R зависимы.

Например, мы запустили тест позавчера. Если мы проводили тест правдоподобий вчера, получив R_{вчера}, то новый тест сегодня будет использовать данные сегодняшнего дня + данные прошлых дней. В этом смысле наша вновь подсчитанная статистика R_{cегодня} зависима с предыдущей R_{вчера}.

Обычный ход, имея зависимые данные, это взять среднее:

$\bar{R}=\frac{\sum_{i=1}^{n}R_{i}}{n}$

Мы можем вернуться легко во фреквенсистиский подход, получив распределение R при верности H0. Будем генерировать из одной популяции выборки А и B, считать Ratio по (1). У нас получится примерно такое распределение, LogGamma:

Примечательно, что аппроксимацией p-value может быть:

$p\simeq \frac{1}{R}$

Например:

$p\simeq \frac{1}{20}=0.05$

В целом, если смотреть на распределение, то весьма похоже. Wilson ссылается на теорему Wilks’, которая утверждает, что если у нас общая нулевая гипотеза для всех тестов правдоподобий, то распределение R будет LogGamma (ɑ=v/2, 𝛃=1). И при v=2 (-> ɑ=1):

$p^\circ =\frac{1}{R}$ $R=\frac{1}{p^\circ}$

Перепишем тогда среднее R:

$\bar{R}=\frac{\sum_{i=1}^{n}\frac{1}{p_{i}}}{n}$ $\frac{1}{p_{\circ}} =\frac{\sum_{i=1}^{n}\frac{1}{p_{i}}}{n}$ $p_{\circ} =\frac{n}{\sum_{i=1}^{n}\frac{1}{p_{i}}}$

Готово, мы получим harmonic mean p-value (HMP).

Важно: обозначается как p_0, потому что интерпретировать HMP буквально как p-value нельзя. Это можно сделать тогда, когда оно достаточно маленькое (когда оно в привычных нам значениях от 0.05 и меньше). При большем уровне значимости приравнивать p_0 к p_value грозит большим кол-вом ошибок 1-го рода.

Скрытый текст

В этом случае вам следует, при условии множества тестов L, использовать формулу для расчета точного p_{p0} на базе гармонического. Подробнее см. тут, там же есть таблица для определения значимости от L.

Возвращаемся к формуле: нам ничего не мешает ввести веса. Так как n — это сумма того, сколько статистик у нас от каждого теста, то мы можем это n переписать следующим образом:

$n=1_{x_1}+1_{x_2}, \space \space w_{1,2}=1$ $n=w_1{1_{x_1}}+w_2{1_{x_2}}$ $H(p_{1}, p_{2})=\frac{\sum_{1}^{2}w_{i}}{\frac{1}{{p}_{1}}+\frac{1}{{p}_{2}}}$ $H(p_{1}, p_{2})=\frac{\sum_{1}^{2}w_{i}}{\frac{w_{1}}{{p}_{1}}+\frac{w_{2}}{{p}_{2}}}$ $H(p_{1}, p_{2})=\frac{\sum_{1}^{2}w_{i}}{\sum_{1}^{2}\frac{w_{i}}{{p}_{i}}}$

Осталось только нормализовать веса для суммы = 1:

$w_{norm_i}=\frac{w_{i}}{\sum_{i=1}^{n}w_{i}}$

Вес в нашем случае определяется через размер выборок в тестах.

Итого, формула гармоническое среднего для общего случая по аналогии следующая:

$H(p_{1}, ..., p_{k})=\frac{\sum_{i=1}^{k}w_{i}}{\sum_{i=1}^{k}\frac{w_{i}}{{p}_{i}}}$

Применение

Теперь вернёмся к нашему примеру:

Веса как доли от total будут такими:

$\color{green}{w_{1}=\frac{20}{100}=0.2}, \space \color{red}{w_{2}=\frac{80}{100}=0.8}$ $H(p_{1},p_{2})=\frac{\sum_{i=1}^{k}w_{i}}{\sum_{i=1}^{k}\frac{w_{i}}{{p}_{i}}}=\frac{1}{\frac{0.2}{0.03}+\frac{0.8}{0.07}}=\frac{1}{6.66+11.42}=0.055$

Ага, уже не так и значимо 🙂

Ещё раз стоит напомнить, что этот метод полезен в случае, если идёт проверка однородности и для доп. оценки. Гармоническое среднее зависимых тестов p-value здесь будет как раз кстати. Более того, вы можете ввести и веса, но не на основе размера выборки (очевидно, они будут равны в этом случае = 01), а на основе, например, того, что для вас важнее по однородности, соц. дем или метрики.

Заключение

Мы рассмотрели мета-анализ и базовые методы проверки общей H0. С их помощью мы можем объединять результаты различных исследований для получения более весомых выводов о нашем воздействии. Мета-анализ повышает не только уровень доказательности, но и мощность наших тестов.

Однако надо помнить, что прежде, чем применить тот или иной метод, вы должны сначала:

Во-первых, определить, действительно ли у ряда ваших тестов общая H0, чтобы провести мета-анализ, иначе вы рискуете сделать невалидное заключение. И это самая сложная часть, так как статистика ничего про это не знает и методов определения общей H0 не имеет. Это можете сделать только вы как исследователь. В общем случае рекомендуем перед применением того или иного теста привести ряд аргументов в пользу того, почему вы можете подвергнуть результаты тестов мета-анализу.

Во-вторых, надо оценить, зависимы ли наши тесты или нет, чтобы применить подходящий метод.

В-третьих, выбор теста зависит и от типа данных.

Методов много, но самые ходовые — это Fisher, Shouffer»s weighted Z, Harmonic Mean P‑value. Наиболее вероятный для использования в бизнесе с учётом классических проверок средних — это Shouffer»s weighted Z.

Спасибо за ревью Антону Денисову, Нурлану Садыкову, Диме Чернышеву и Валере Захарову; Егору Мелехину и Ивану Щербаку за проверку на понимание и правки в расчётах; и Никите Суркову за анализ выводов, прежде всего мат. выводов и их логику.

Также благодарим Анастасию Фёдорову за редакцию материала.

Использованные в статье материалы

Fisher, “Statistical Methods for Research Workers”, 5th Edition
М. Б. Лагутин, «Наглядная математическая статистика»
Hedges, Olkin, “Statistical Methods for Meta‑Analysis”
Brainder, “The logic of the Fisher method to combine P‑values”
Thiagarajan, “Using weights p‑values in Fisher”s Method”
Heard, Rubin‑Delanchy, “Choosing Between Methods of Combining p‑values”
Mudholkar, George, “The Logit Statistic for Combining Probabilities”
Winkler “Non‑Parametric Combination for Analyses of Multi‑Modal Imaging”
Zezhong, “Increase A/B Testing Power by Combining Experiments”
Whitlock, “Combining probability from independent tests: the weighted Z‑method is superior to Fisher’s approach”
Wilson, “The harmonic mean p‑value for combining dependent tests”

ссылка на оригинал статьи https://habr.com/ru/articles/862202/

Гайд по мета-анализу результатов тестов

Мотивация к использованию

Комментарий к размышлению

Подводные камни

Общая H0: независимая и зависимая

Проверка независимой общей H0

Метод Типпета (Tippets method)

Метод Фишера (Fisher’s method, Fisher’s combined probability test)

Учёт разного объёма выборок

Наглядные преобразования

Небольшой подводный камень метода Фишера

Метод Пирсона (Pearson’s Method)

Метод Mudholkar–George

Weighted Z-score (Shouffer’s)

Почему, возможно, он больше подходит, чем Фишер

Обзор H0 c критическими областями для комбинации из двух p-value для методов, которые на слуху, с альфой = 0.05

Что выбрать-то?

Проверка зависимой общей H0

Harmonic Mean P-value (HMP)

Вывод метода

Применение

Заключение

Использованные в статье материалы

Комментарии

Добавить комментарий Отменить ответ