Математический подход приоткрыл «чёрный ящик» принятия решений ИИ

Западные исследователи разработали новую методику, позволяющую с помощью математики понять, как именно нейронные сети принимают решения.

Многие современные технологии, от цифровых помощников Siri и ChatGPT до медицинской визуализации и самоуправляемых автомобилей, основаны на машинном обучении. Однако логику «рассуждений» нейронных сетей, лежащих в основе этих систем машинного обучения, трудно понять. Исследователи часто называют ИИ «чёрными ящиками» среди исследователей.

«Мы создаём нейронные сети, которые могут выполнять конкретные задачи, оставляя себе возможность решать уравнения, управляющие их деятельностью, — говорит Лайл Мюллер, профессор математики и директор Западной лаборатории сетевых наук Филдса, входящей в состав недавно созданного Центра сотрудничества Филдса и Запада. — Это математическое решение позволяет нам «открыть чёрный ящик» и понять, как именно сеть делает то, что она делает».

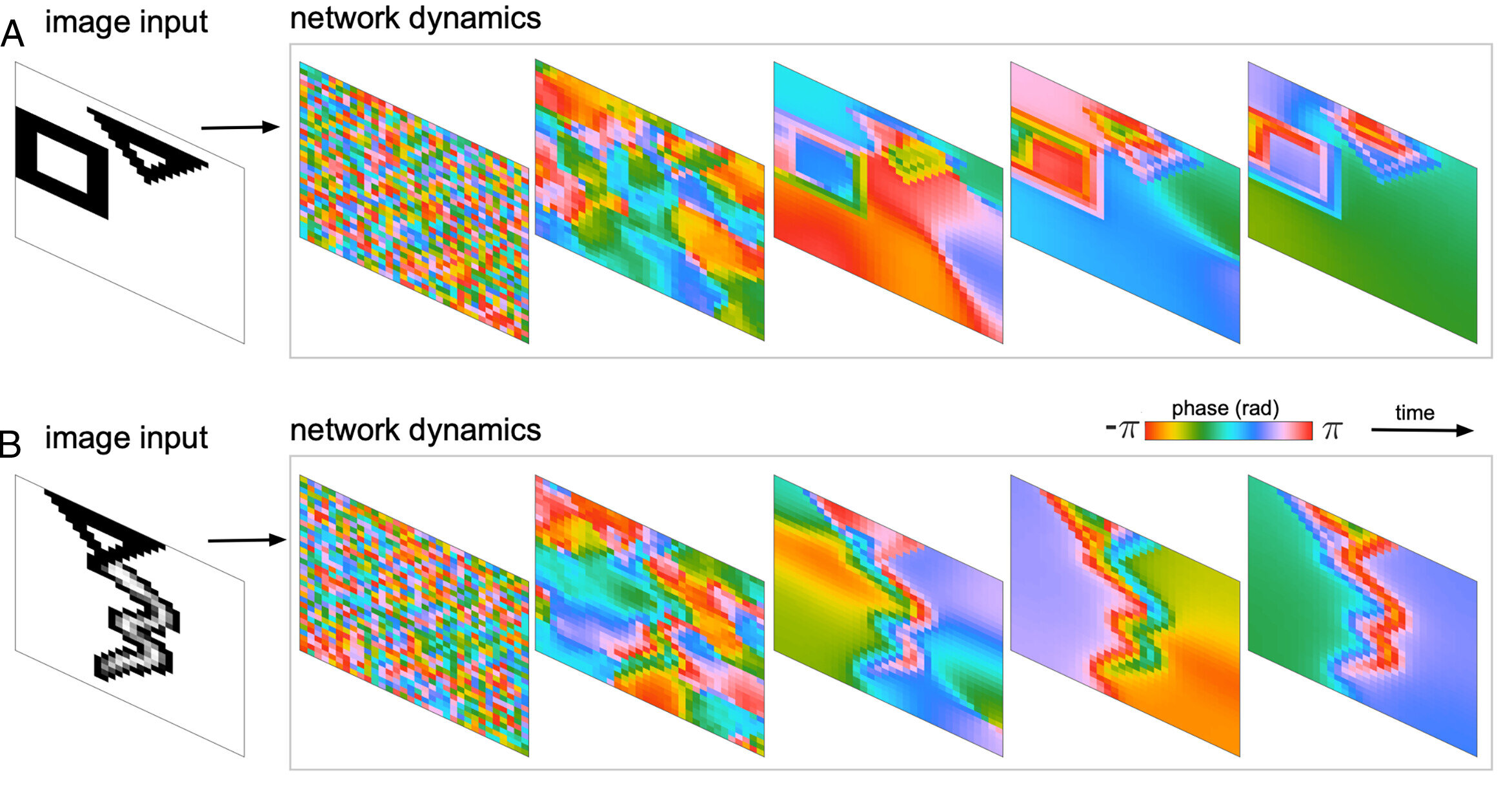
Западная команда, в которую вошли Мюллер, постдокторанты Луиза Либони и Роберто Будзински, а также аспирант Алекс Буш, впервые продемонстрировала это новое достижение на задаче сегментации изображений — фундаментальном процессе в компьютерном зрении, когда системы машинного обучения разделяют изображения на отдельные части, например, отделяют объекты на изображении от фона.

Начав с простых геометрических фигур, таких как квадраты и треугольники, они создали нейронную сеть, способную сегментировать эти базовые изображения.

Затем Мюллер и его коллеги использовали математический подход, который они ранее разработали для изучения других сетей, чтобы исследовать, как новая сеть выполняет задачу сегментации при анализе этих простых изображений.

Математический подход позволил команде точно понять, как происходит каждый шаг вычислений. К некоторому удивлению, команда обнаружила, что сеть также может сегментировать — или видеть и интерпретировать — несколько естественных изображений, таких как фотографии белого медведя, идущего по снегу, или птицы в дикой природе.

«Упростив процесс, чтобы получить математическое представление, мы смогли построить сеть, которая была более гибкой, чем предыдущие, а также хорошо справлялась с новыми входными сигналами, которые она никогда не видела», — говорит Мюллер, сотрудник Западного института нейронаук.