Процедурная генерация двухмерной полигональной карты

Предисловие

Привет Хабр ! Это моя первая статья на тему процедурной генерации. Здесь я рассмотрю конкретную задачу по генерации, её решение и опишу ключевые использованные принципы. Пишу эту статью для того, чтобы поделиться идеями и опытом, которых мне не хватало, когда я взялся за дело две недели назад. Я не буду делать полный разбор проекта, а лишь опишу и визуализирую принцип.

О проекте

Картинка, представленная в начале — это результат работы моего алгоритма, предназначенного для моей игры, им я не стал делиться, ибо он плохо оптимизирован, запутан, а доведение до презентабельного вида займёт уйму времени. Писал на Python, использовал сторонние библиотеки: Shapely — для работы с геометрией, диаграмм Вороного (документация); networkx — для работы с графами, это понадобиться для прокладки дорог (документация); perlin_noise — шум Перлина, matplotlib — для визуализации (документация).

Описание задачи

Из себя карта представляет квадрат размером 32 на 32 клетки (клетки нужны будут впоследствии для индексации объектов, на них при генерации внимания не обращаем). На карте должны располагаться: 6 обычных островов, 6 «архипелагов» — группы островов, в которых есть один центральный основной и несколько малых островков, 2 главных острова — базы двух команд, они выходят за границы карты. Таким образом на карте должно быть 12 ключевых остров, за которые будут вестись бои и на которых должны располагаться порты как спавнпоинты и точки захвата. Помимо портов, на островах должны располагаться населённые пункты, от них всегда должна быть возможность добраться до порта. Два главных острова должны содержать большой порт и город, а также должны находиться в противоположных углах карты. В случае архипелагов, если населённый пункт расположен не на главном острове, к главному острову строится мост. Доступные объекты представлены на картинке:

• (B) Берег — участок суши, задаётся последовательностью координат вершин.

• (G) Лужайка, задаётся последовательностью координат вершин.

• (S) Камень — естественное препятствие, задаётся аналогично «B».

• (C) Фундамент — задаётся последовательностью координат вершин.

• (_) Мост — задаётся двумя точками.

• (T) Дерево — задаётся координатой, id типа (пальма, дуб, сосна), размером (1,2,3,4).

• (#) Постройка — задаётся координатами центра, направлением, шириной, высотой, id типа (дом, грузовой контейнер, ангар, погрузочный кран).

Основные правила

• Острова не пересекаются, между ними есть минимальное расстояние.

• Порты находятся на приличном удалении друг от друга, ситуация, когда один причал стоит в притык к другому — недопустима.

• В архипелагах дочерние острова не могут располагаться далеко от главного, всегда можно построить мост.

• Порт на каждом острове одинаковый, пирс не может подходить слишком близко к другим островам.

• Все острова кроме главных находятся в пределах карты.

• Чтобы алгоритм не зависел от размера карты, в большинстве случаев я буду принимать длину стороны карты за единицу и на этом строить расчёты.

Словарик

• Базовый / главный остров — большой остров в углу карты с большим портом, городом. На карте таких может быть только 2.

• Ключевой остров — остров, на котором есть порты, может являться основным островом в архипелаге.

• Много где будет встречаться константа WH — это ширина и высота мира в клетках. Мы принимаем WH = 32.

Этап №0 Разметка

На этом этапе и на многих последующих мы будем использовать диаграмму Вороного (Диаграмма Вороного).

Первым делом, очевидно, нужно расположить острова. Но как? Случайно рисовать острова и проверять пересечения с уже существующими ? В таком случае потребуется множество итераций, времени и результат будет непредсказуем. Поэтому, первым делом лучше заняться не островами, а секторами, внутри которых в свою очередь будут располагаться острова, архипелаги и главные острова. Разбивая карту на фиксированное количество секторов, мы можем точно определить сколько ключевых остров будет на карте.

Расставим 12 случайных точек на карте, построим по ним диаграмму Вороного. Для того, чтобы главные острова гарантированно существовали и находились в углах карты, добавим 2 точки на небольшом отдалении от нужных нам углов.

MAP_SQUARE = shapely.geometry.Polygon([(0, 0), (1, 0), (1, 1), (0, 1)]) points = [(0.1, 0.1), (0.9, 0.9)]  for _ in range(0, 12):   while True:     x = random.random()     y = random.random()     dst = x + y     if ((1 - abs(1 - dst)) ** 2) > random():       # Отдаление точки от диагонали карты влияет на вероятность её появления.       # Чем дальше от диагонали, тем меньше вероятность появления.       points.append((x, y))       break base_points = shapely.geometry.MultiPoint(points) sectors = shapely.ops.voronoi_diagram(base_points) sectors = list(map(lambda p: p.intersection(MAP_SQUARE), sectors.geoms))

Для главных остров нам нужно выделять довольно много места, значит 12 произвольных точек должны располагаться как можно дальше от предполагаемых главных островов, то бишь ближе к диагонали. Таким образом отдаление точки от диагонали карты влияет на вероятность её появления. Чем дальше от диагонали, тем меньше вероятность появления. (Визуализация распределения точек через график) Также убедимся, что площадь самого маленького сектора более 0.1*0.1.

Хорошо, теперь имеем 14 секторов, 2 на главные острова, остальные 12 на остова и архипелаги. Сортируем регионы по занимаемой площади: 6 самых больших резервируются под архипелаги, оставшиеся 6 под обычные острова. На этом моменте убедимся, что сектора главных островов соответствуют условиям:

• Отношение большего сектора главного острова к малому меньше 1.25. Это гарантирует, что главные острова будут схожей площади и обе команды будут находиться в равных условиях.

• Отношение площади сектора главного острова к площади его рамки больше 0.6. Если оно равно 0.5, то сектор имеет форму треугольника, если равно 1, то форму квадрата.

1. ♦ (ромб) — сектор архипелага

2. ● (круг) — сектор обычного острова

3. x (крестик) — сектор главного острова

Этап №1 Рисуем острова

Мы разбили карту на секторы, и теперь будем работать с каждым сектором по отдельности, начнём с секторов, зарезервированных под обычные острова. Задача проста: расположить остров в центр сектора таким образом, чтобы от острова до границ сектора оставалось пространство. Как создать необычную форму? Эту задачу я очень некрасиво решил ещё 2.5 года назад:

def clip(x, min, max): # Функция ограниччивает число x сверху и снизу     if (min > max):return x     elif (x < min):return min     elif (x > max):return max     else:return x  def lookat(x, y): # Определяем направление вектора (или же из точки (0,0) в точку (x,y))     if x == 0:x = 0.001     angle = math.atan((y / x)) / (math.pi / 180)     if y != abs(y):angle = angle + 360     if x != abs(x):angle = angle + 180     return angle % 360    def generatePolygon(cx, cy, radius, irregularity, spikeyness, numVerts):     irregularity = clip(irregularity, 0, 1) * 2 * math.pi / numVerts     spikeyness = clip(spikeyness, 0, 1) * radius     angleSteps = []     lower = (2 * math.pi / numVerts) - irregularity     upper = (2 * math.pi / numVerts) + irregularity     sum = 0     for i in range(numVerts):         tmp = random.uniform(lower, upper)         angleSteps.append(tmp)         sum = sum + tmp     k = sum / (2 * math.pi)     for i in range(numVerts):         angleSteps[i] = angleSteps[i] / k     points = []     angle = random.uniform(0, 2 * math.pi)     for i in range(numVerts):         r_i = clip(random.gauss(radius, spikeyness), 0, 2 * radius)         x = cx + r_i * math.cos(angle)         y = cy + r_i * math.sin(angle)         points.append((x, y))         angle = angle + angleSteps[i]     return points  def generatePolygon2(p):     points = []     cx, cy = 0, 0     for sim in p:         cx += sim[0]         cy += sim[1]     cx = cx / len(p)     cy = cy / len(p)     for _ in range(0, len(p)):         points.append(p[_])         d = (math.sqrt((p[int((_ + 1) % len(p))][0] - cx) ** 2 + (p[int((_ + 1) % len(p))][1] - cy) ** 2) + math.sqrt((p[_][0] - cx) ** 2 + (p[_][1] - cy) ** 2)) / 2         d0 = lookat(p[_][0] - cx, p[_][1] - cy)         d1 = lookat(p[int((_ + 1) % len(p))][0] - cx, p[int((_ + 1) % len(p))][1] - cy)         if abs(d0 - d1) > 180:             if d0 < d1:                 d0 += 360             else:                 d1 += 360         d2 = ((d0 + d1) / 2) % 360         d3 = math.sqrt((p[_][0] - p[int((_ + 1) % len(p))][0]) ** 2 + (p[_][1] - p[int((_ + 1) % len(p))][1]) ** 2) / d         points.append([cx + math.cos(d2 / 180 * math.pi) * d * d3, cy + math.sin(d2 / 180 * math.pi) * d * d3])     return points # Сглаживание полигона p, где p - последовательность координат, res - сила сглаживания.  def smoothPolygon(p, res):       points = []     for _ in range(0, len(p)):         a0 = p[_][0] + (                 (((p[(len(p) + _ - 1) % len(p)][0] + p[_][0]) / 2 + (p[(_ + 1) % len(p)][0] + p[_][0]) / 2) / 2) -                 p[_][0]) * res         a1 = p[_][1] + (                 (((p[(len(p) + _ - 1) % len(p)][1] + p[_][1]) / 2 + (p[(_ + 1) % len(p)][1] + p[_][1]) / 2) / 2) -                 p[_][1]) * res         points.append([a0, a1])     return points  def segments(seq): # Возвращает shapely.geometry.LineString каждой стороны.     return list(map(LineString, zip(seq.coords[:-1], seq.coords[1:])))  # СОЗДАНИЕ ОСТРОВА ln = LinearRing(list(sector.exterior.coords[:])) dst = 1 # Тут ищем минимальное расстояние от центра региона до его стороны. for line in segments(ln):     dst = min(sector.centroid.distance(line), dst) size = random.randint(6, 9) * 0.1 vertices_cnt = round(10 * max(1, (sector.area / 0.05) ** 0.5)) pnt = sector.centroid p = generatePolygon2(generatePolygon(pnt.x, pnt.y, dst * size, 0.5, 0.5,vertices_cnt)) for _ in range(0, 2):p = smoothPolygon(p, 2) for _ in range(0, 2):p = smoothPolygon(p, 1)  island = shapely.geometry.Polygon(p)

С секторами обычных островов готово, везде по острову, такую же операцию мы проделываем в секторах архипелагов. Дочерние острова я добавлял просто отбирая лучшие варианты расположения из 100 просчитанных, учитывая правило: от нового острова до любого старого расстояние больше 0.5wh и меньше 1wh. Это нужно для того, чтобы между островами можно было строить мосты.

Главные острова создаются немного по другому: центр острова располагается не в центре региона, а в углу карты, соответственно, мы будем опираться не на центр региона, а на угол и радиус тоже будем считать от него.

Для каждого участка суши нужно также создать лужайку, это делается через shapely.geometry.Polygon.buffer(-0.1wh) лужайка отображена зелёной линией.

1. Синий крест — центр региона

2. Жёлтый крест — центр острова (может не совпадать с изначальным)

Этап №2 Расположение портов

Далее будем рассматривать, как пример, один остров (мне нравиться его форма, я считаю её самой близкой к желаемой).

Требуется расположить 12 портов, по одному на каждый ключевой остров (порты на главных островах затронем ниже). Структура порта должна содержать пирс и платформу, платформа может касаться воды только с той стороны, с которой расположен пирс. С платформы должно быть доступно 3 выезда с трёх сторон, но она должна касаться воды. Расстояние от пирса до ближайшего острова должно быть более 0.5wh. К нему должна быть возможность подплыть с двух сторон.

Самое простое решение:

1. Перебираем каждую грань острова, из её центра по направлению вектора нормали строим пирс. Если он не касается другого острова или границы сектора, сохраняем его.

2. Для каждого сохранённого положения порта (красный) считаем расстояние до границы сектора и расстояние до центра острова. Сортируем сохранённые конфигурации по ключу, порт первый в списке «строим». Отбирая порт по близости к центру острова, мы увеличиваем вероятность его появление в заливе. Отбирая порт по удалению от границы, нужно, чтобы порт находился как можно ближе к центру сектора.

def key(seaport):     return seaport.pier.distance(island.centroid) + 0.5 * ((island.centroid.distance(         shapely.geometry.LinearRing(sector.exterior.coords))) - seaport.pier.centroid.distance(         shapely.geometry.LinearRing(sector.exterior.coords)))

Постройки, расположенные в порту на рисунке не отмечены.

Этап №3 Разметка будущих дорог

Дольше всего я думал именно над этим этапом, так как расположение дорог определяет расположение домов и прочих объектов. Дороги должны куда-то вести, их построение должно быть максимально рациональным. Непонятное расположение дорог сильно бросается в глаза. Из этого следует первая идея: первым делом не дороги, а пункты назначения для этих дорог.

У нас уже есть на каждом ключевом острове минимум один пункт назначения — порт, можно также проводить дороги к предполагаемым мостам. Оптимальные места для мостов ищутся очень просто: находим ближайшие друг к другу точки точки двух островов, по ним строится мост. Должны быть населённые пункты и дороги к ним.

Я нашёл решение для себя, оно является идеальным для меня компромиссом между простотой реализации и качеством результата. Расставим на острове точки, применим к ним диаграмму Вороного, разобьём таким образом остров на сетку, построим граф по этой сетке и будем представлять дороги как последовательность рёбер этого графа.

1. Мы выделяем область внутри лужайки, делая небольшой отступ от сторон. Это нужно для того, чтобы будущие дороги не касались песка, не выходили слишком близко к берегу. Назовём эту область «дорожной зоной».

2. Прежде чем расставлять в дорожной зоне точки, нужно создать условия, при которых всегда можно построить дороги к пунктам назначений. То есть граф дороги при любой генерации должен касаться порта, желательно ещё и в определённых местах, также он должен подходить к точкам, из которых будут строиться мосты. Диаграмма Вороного работает так, что если построить её по двум точкам, то линия пройдёт ровно между ними и перпендикулярно прямой, лежащей на этих точках. То есть, мы можем не выдумывать что-то своё, а просто проставить несколько точек в нужные места так, чтобы дороги проходили там, где нам нужно. В случае порта, поставим точки по углам платформы, дороги в любом случае будут заходить на платформу ровно через центры её сторон и перпендикулярно этим сторонам. С мостом принцип такой же.

3. Расставляем точки. Нужно лишь следить, чтобы точки не стояли слишком близко друг к другу, к платформе (я немного нарушил это правило, как видно на картинке). Точки на платформе стоять не должны, иначе красивых выездов из порта не будет.

4. Создаём сетку, применяя диаграмму Вороного к расставленным точкам.

5. Строим граф по получившейся сетке, сохраняем все получившиеся многоугольники (с ними мы будем работать при генерации домов). При создании графа, задаём каждому ребру вес равный его длине.

Так выглядит карта на данном этапе.

1. Зелёные точки — проставленные нами точки (я их расставляю по всему острову, но работаю только с участком диаграммы, вошедшим в дорожную зону.)

2. Фиолетовые линии — рёбра графа дорог.

3. Красный полигон — дорожная зона.

Главные острова (этап №2-3)

Локацию для большого порта мы ищем почти также, как и для обычного — ищем самое близкое место к центру острова. Разница лишь в том, что порт больше, платформы две: городская и портовая; и нужно следить, чтобы они не выходили за пределы карты. Дорожные точки расставляются по прямоугольной сетке случайной размерности, расположенной на городской платформе.

Этап №4 Строим дороги

Как я уже говорил, нам нужно проложить дороги так, чтобы их расположение казалось реалистичным. Мы так и сделаем: каждую новую дорогу мы будем вести к ближайшей, уже существующей. Для поиска кратчайшего пути и нужен был взвешенный граф. Проводя дорогу по рёбрам графа, мы будем задавать им нулевые веса, чтобы алгоритм поиска пути «сокращал» свой путь по дорогам и не строил новые.

Перед этим нужно создать больше пунктов назначения — населённых пунктов. Отсортируем все дорожные регионы острова по площади и отметим несколько самых маленьких (слишком маленькие пропускаем) и те, что касаются платформы порта как городские. Весам, прилегающих к ним рёбер, зададим нулевые значения, отметим их как дороги.

И только после этого шага мы проходимся по каждому городскому региону и строим от любой его вершины дорогу до порта. После этого строим дороги от порта до всех предполагаемых мостов. Строим мосты. Если остров слишком маленький или на нём нет поселения, мост не строим.

В том случае, если на острове портов нет, то строим дороги от городских регионов к мосту.

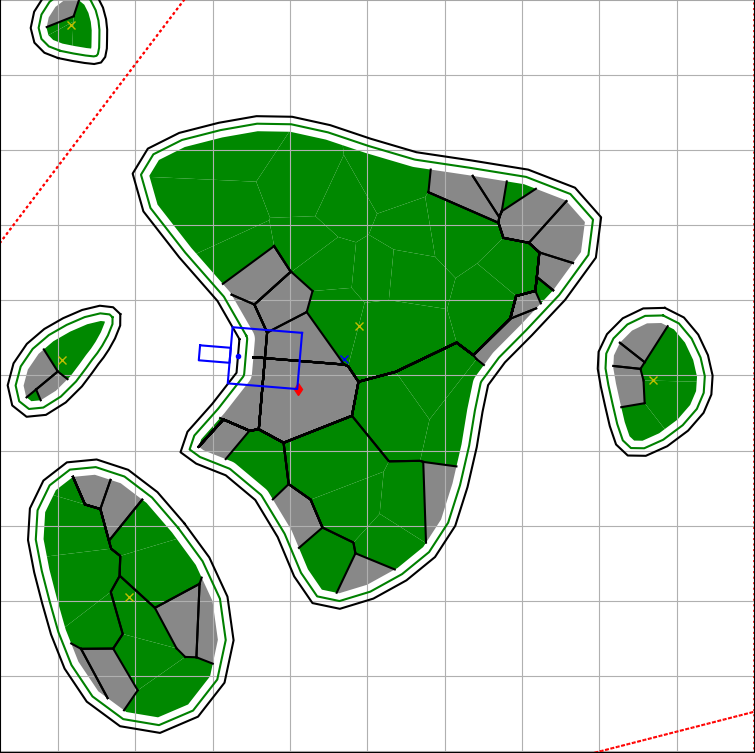
1. Серые многоугольники — городские регионы

2. Зелёные многоугольники — обычные регионы

3. Чёрные линии — дороги

4. Мосты тут не отображаются, но места их соединений с островами хорошо видны.

Этап №5 Заполняем объектами регионы

Для создания объектов добавим правила:

• Объект находится внутри дорожного региона.

• Расстояние объекта от ближайшей границы всегда больше 2/3 ширины дороги. Это правило гарантирует, что объекты не будут касаться дорог. Также оно гарантирует, что на острове не будет длинных непреодолимых цепей из объектов, все объекты можно будет объехать, двигаясь по рёбрам дорожной сетки.

• Объекты не пересекают уже существующие структуры (порт, и.т.п).

Домики

Напоминаю, все домики имеют прямоугольную форму и могут быть направлены в любую сторону.

В городских регионах всё просто, мы проходимся по всем граням региона по кругу несколько раз и, отступая от грани минимальное расстояние, пытаемся построить дом. Если предполагаемый дом находится слишком близко к построенным домам или пересекает их, постройка отменяется. Расстояние между домами не может быть меньше минимальной ширины проезда, в моём случае это 2/3 ширины дороги.

В лесных регионах мы тоже строим дома, по тому же правилу, что и в городских, но опираясь только на те грани, которые являются также гранями городских регионов.

Камни

С камнями интереснее, случайным образом натыкать их внутри региона — нельзя, так как камни будут наслаиваться друг на друга и могут формировать из себя замкнутые цепочки, ещё будет слишком явно видно, где лежит дорожная сетка.

Для того, чтобы правильно расположить камни, сначала представим их как окружности. Начнём случайно располагать окружности разного радиуса внутри региона, а сохранять будем только если:

• Расстояние от поставленной окружности до всех сохранённых, с которыми она не пересекается, больше или равно минимальной ширине проезда (она у нас равна 2/3 ширины дороги).

• Поставленная окружность пересекается не более, чем с тремя сохранёнными окружностями.

• Радиус всех пересекаемых сохранённых окружностей больше радиуса поставленной.

• Отношение площади пересечения поставленной и каждой пересекаемой сохранённой окружности к площади этой сохранённой окружности находится в переделах 0.05 и 0.25. Это нужно, чтобы камни не сильно наезжали друг на друга.

• Камень не пересекает постройки.

После расстановки всех окружностей делаем из них многоугольники: расставляем на окружности несколько точек (количество зависит от размера), по ним строим многоугольник. Если площадь получившегося многоугольника меньше, чем 7/10, расставляем точки заново.

Количество камней для каждого региона задаётся случайно.

rocks_amount = random.randint(1, 5) ** 2

Этап №6 Лесопосадка

Деревья задаются их типом, размером и одной точкой.

Требуется, чтобы разные деревья росли с разной частотой в разных местах. К примеру: пальмы растут только в городских кварталах, сосны только вне города. На острове есть участки, где деревьев нет. Деревья не могут располагаться слишком близко друг к другу.

В обычном регионе

Аналогично камням, количество деревьев в регионе случайно:

trees_amount = random.randint(2, 8) ** 2

Подбираем кроне дерева случайный размер:

WH = 32 sizes_of_stages = {     0: 0.1,     1: 0.15,     2: 0.2,     3: 0.25, } stage = random.randint(1, 5) if stage == 5:     if random.random() > 0.5:         stage = 0     else:         stage = 3 else:     stage = math.ceil(stage / 2) r = sizes_of_stages[stage] / WH

Случайно располагаем точки внутри региона, если все условия соблюдаются, то сохраняем точку:

• Расстояние от точки до границы региона больше минимальной ширины проезда.

• Точка не стоит в доме или в камне, или в порте.

• Если крона поставленного дерева пересекает кроны не более трёх сохранённых деревьев.

• Если крона дерева не задевает ни одного, то, с вероятностью 50%, дерево не сохраняем. Это нужно, чтобы было меньше деревьев-одиночек.

• Дерево не находится внутри другого (большего по размеру).

• Расстояние между поставленной точкой и остальными сохранёнными более 0.04wh. Деревья не будут расти одно в другом.

Красим деревья, для этого ориентируемся на шум Перлина и случайность:

TREETYPE_NOISE = perlin_noise.PerlinNoise(octaves=30) if TREETYPE_NOISE([x, y]) + random.random() * 0.4 - 0.3 > 0:     type = 0 # Дуб else:     type = 1 # Сосна

В городском регионе

Деревья создаются также, как и в обычном регионе, только значения другие:

trees_amount = random.randint(3, 5) ** 2

WH = 32 sizes_of_stages = {     0: 0.1,     1: 0.15, } stage = randint(0, 1) r = sizes_of_stages[stage] / WH

TREETYPE_NOISE = perlin_noise.PerlinNoise(octaves=30) if TREETYPE_NOISE([x, y]) + random.random() * 0.4 - 0.3 > 0:     type = 2 # Пальма else:     t  ype = 0 # Дуб

Победа !

Послесловие

Если вы захотели сделать случайную генерацию мира для вашей игры, вам стоит ещё семь раз подумать. Определитесь с вашей задачей. Мне этот алгоритм нужен для генерации прототипа карты. Подразумевается, что сгенерированную карту я вручную просмотрю и исправлю некоторые ошибки, которые будут. Так как карты я планирую менять часто, я счёл, что лучше потратить две недели на алгоритм, который сэкономит мне многие дни нудной работы. Стоит ли вам ради одной сгенерированной карты писать алгоритм? Чтобы создать по-настоящему хороший генератор, нужно потратить огромное количество времени и нервов, тестируя и отлаживая алгоритм. Ни в коем случае не рассматривайте это как лёгкую прогулку !

Что и как можно улучшить и поменять?

1. Дробить мир на меньшие тайлы. Генерировать мир с тайлами проще, чем без них. Изначально их у меня в мире не было, поэтому я их создал: разделил карту на островные зоны, разделил острова на дорожные регионы. Но ведь это не предел, каждый дорожный регион можно разделить ещё раз и ещё раз. Чем больше мы разделяем мир на тайлы, тем меньше нам нужно будет потом полагаться на случайный подбор позиций для объектов. Пример: разделив обычный регион на несколько частей, можно в центре этих субрегионов создавать камни, не перебирая огромное множество возможных позиций.

2. Можно добавить другие типы дорожных регионов и усложнить правила выбора их типов, к примеру: индустриальный и фермерский. Сложность в том, чтобы наилучшим образом распределить регионы между собой. Так как остров на данном этапе состоит из тайлов, хотя и произвольной формы, для распределения типов здесь можно приспособить методы, свойственные больше генерации по квадратным тайлам (коллапс волновой функции, и.т.п).

3. Применение шума Перлина. Значения шумов могут помочь определять средний размер домов, густоту дорожных точек на острове, размерность и густоту посадки деревьев, частоту расположения камней и не только.

4. Дороги можно проводить не по граням дорожных регионов, а через их центры. Это позволит гораздо больше контролировать расположение дорог.

Что дальше ?

Хотел бы поделиться ссылками на статьи, где рассматриваются идеи, которые можно подключить к уже существующему алгоритму.

• Как создавать большие реалистичные острова со сложным рельефом

• Процедурная генерация планет со сложным ландшафтом — Планета здесь разделяется на множество тайлов-многоугольников.