Рекурсивно самовычисляющая Вселенная Стивена Вольфрама – теория всего или теория чего угодно?

«Я думаю, что вычислениям суждено стать определяющей идеей нашего будущего» (Стивен Вольфрам)

«Мой друг Джонни фон Нейман говорил, бывало, что имея в формуле четыре свободных параметра, он может подогнать её хоть под слона, а если параметров будет пять, то этого слона можно заставить ещё и хоботом шевелить» (Энрико Ферми)

«Есть теория, согласно которой в том случае, если кто-то точно выяснит, для чего и зачем появилась Вселенная, она тут же исчезнет, и её заменит нечто другое, ещё более бессмысленное и необъяснимое.
Есть другая теория, согласно которой это уже произошло» (Дуглас Адамс)

В 2020 г. во многих средствах массовой информации писали об очередной «теории всего» – гипотезе рекурсивно самовычисляющей Вселенной. Её автор – известный бизнесмен и программист Стивен Вольфрам, который разработал базу знаний Wolfram Alpha и ПО Mathematica. Особенно большой ажиотаж вызвала статья «Кажется, мы близки к пониманию фундаментальной теории физики, и она прекрасна», переведенная для Хабра уважаемым @SergioShpadi 448-страничный технический документ, загруженный на arxiv.org, называется скромнее: «Класс моделей, потенциально представляющих фундаментальную физику». Он переполнен странными графическими изображениями, но не содержит ни одной математической формулы. Что это вообще такое – наука нового типа или причудливое увлечение миллиардера? Это теория одной или множества вселенных? Как она соотносится с теорией Эверетта и другими интерпретациями квантовой механики? Светит ли ей признание официальной наукой, или она войдёт в историю как образец псевдонаучной (гипер)графомании? Может ли наш мир оказаться подобием Майнкрафта, японского сканворда или головоломки «соедини точки по цифрам»»?

Стивен Вольфрам уже много лет жалуется, что физики его игнорируют и не хотят писать отзывы на его работы. Неужели это признак глобального заговора учёных, не желающих менять старую парадигму мышления? Я не физик и не математик, чтобы делать выводы о корректности всех моделей, но и теория у Вольфрама не такая сложная, чтобы не разобраться в ней без специального образования. На мой взгляд, Вольфрам заслуживает более пристального внимания, ведь его модель весьма показательна как пример того, как далеко можно зайти в поисках дискретной и детерминированной основы физической реальности. Поэтому представляю вам свой философский обзор и объяснение теории рекурсивно самовычисляющей Вселенной на естественном языке.

Клеточные автоматы

В статье «Квантовый панкомпьютерализм против цифровой физики» я уже рассказывал о предыдущих попытках объяснить Вселенную как вычислительную систему, в основе которой лежит не энергия и не материя, а информация и правила её обработки. Я разделил эти концепции на две группы: 1) «всё из кубита», представленная квантовым панкомпьютерализмом Сета Ллойда и Дэвида Дойча; 2) «всё из бита», представленная одноимённой гипотезой (“it from bit”) Джона Уилера, цифровой философией Эдварда Фредкина, цифровым панкомпьютерализмом Юргена Шмидхубера и гипотезой симуляции Ника Бострома. Главное различие между этими подходами состоит в том, что первые исходят из непрерывности физических симметрий, пространства времени и спектра квантовых состояний, а вторые постулируют, что Вселенная фундаментально дискретна и пикселизирована, как мелкомасштабный вид экрана смартфона или монитора компьютера. Каждая клетка – неделимый участок пространства планковской длины, содержащий или не содержащий некий элементарный «атом» пространства – один бит информации.

Идея Вселенной как огромного цифрового компьютера была впервые предложена в 1969 г. Конрадом Цузе в книге «Вычислительное пространство». Затем её развивал Эдвард Фредкин, автор термина «цифровая физика» и руководитель лаборатории компьютерных наук Массачусетского технологического института.

 «Я не верю, что существуют такие объекты, как электроны и фотоны, и вещи, которые являются собой и ничем иным. Я верю, что существует информационный процесс, и биты, когда они находятся в определённых конфигурациях, ведут себя как то, что мы называем электроном, или атомом водорода, или как угодно ещё».

«Конечная природа — это гипотеза о том, что в конечном итоге каждая физическая величина, включая пространство и время, окажется дискретной и конечной; что количество информации в любом малом объёме пространства-времени будет конечным и равным одному из небольшого числа возможностей. (…) конечная природа подразумевает, что базовый субстрат физики работает аналогично работе определённых специализированных компьютеров, называемых клеточными автоматами» (Эдвард Фредкин)

Клеточный автомат – это дискретная вычислительная модель в виде решётки из клеток, каждая из которых в каждый момент дискретного времени находится в одном из конечного числа возможных состояний. Знакомый всем двумерный клеточный автомат – игра в крестики-нолики. Простейший одномерный клеточный автомат напоминает ленту машины Тьюринга, каждая ячейка которой может быть включённой или выключенной. Система эволюционирует дискретными шагами, следуя функциям обновления состояния или динамическим правилам перехода: обновление состояния клетки происходит с учётом состояний других клеток в её локальном окружении. В отличие от машин Тьюринга и обычных компьютеров с архитектурой фон Неймана, клеточные автоматы вычисляют функции и решают алгоритмические задачи параллельно, распределённым образом. На двумерном клеточном автомате можно смоделировать и полный по Тьюрингу компьютер Wireworld с набором универсальных логических элементов (вентилей), предложенный Брайаном Сильверманом в 1987 г.

В 1940-х гг. Джон фон Нейман задумался о механизме самокопирования живых организмов и решил математически описать робота-репликатора, способного производить точные копии самого себя. Следуя предложению своего коллеги Станислава Улама, он сосредоточился на дискретной двумерной системе. Построенный им клеточный автомат представлял собой двумерную решётку, каждая клетка которой могла находиться в одном из 29 состояний. Фон Нейман доказал, что для такой модели существует паттерн, который будет бесконечно копировать самого себя – универсальный конструктор. Он содержит одну строку ячеек, которые служат описанием (подобно ленте Тьюринга) и кодирует последовательность инструкций, которые служат «чертежом» для машины. Машина считывает эти инструкции одну за другой и выполняет соответствующие действия своей «строительной рукой» (другой автомат, который функционирует как операционная система) для создания копии машины без ленты описания в каком-то другом месте решётки. Впоследствии были найдены более простые репликаторы с меньшим числом состояний (8): клеточный автомат Кодда (1968) и петля Лэнгтона (1984).

В 1970 г. математик Джон Конвей представил одну из самых простых вычислительных моделей, когда-либо доказанных как универсальный компьютер – игру «Жизнь». Это двумерный клеточный автомат, в котором заполненные клетки считаются живыми, а пустые – мёртвыми. Игра подчиняется элементарному правилу: мёртвая клетка, с которой соседствуют три живые, сама становится живой, пока с ней соседствуют две или три живые клетки, и умирает, если живых клеток по соседству меньше двух или больше трёх. При определённых начальных конфигурациях это правило порождает интересные и сложные структуры – например, самокопирующиеся глайдеры. Игра «Жизнь» является полной по Тьюрингу, т.е. на этом автомате можно смоделировать любое вычисление из репертуара универсальной машины Тьюринга. Конечно, никто не будет использовать её для расчётов, потому что обычный компьютер намного эффективнее. Но, будучи универсальным компьютером, «Жизнь» определяет наиболее эффективную симуляцию своего собственного поведения. Ни один алгоритм и ни один компьютер не сможет определить по данному ему правилу и начальной конфигурации клеток, к чему приведёт эволюция этого клеточного автомата, пока не смоделирует её пошагово. Определить, достигнет ли когда-нибудь заданная исходная конфигурация в игре «Жизнь» заданной конечной конфигурации – невычислимая задача, как и проблема остановки или занятой бобёр.

В 1977 г. Томмазо Тоффоли впервые использовал обратимые клеточные автоматы для непосредственного моделирования физических систем и законов, которым они подчиняются, а в 1980 г. изобрёл универсальный обратимый вентиль CCNOT, известный как вентиль Тоффоли. Однако в 1981 г. Ричард Фейнман раскритиковал гипотезу Фредкина о Вселенной как обратимом клеточном автомате, отметив, что она не учитывает квантовые процессы, которые нельзя эффективно смоделировать на цифровом компьютере с помощью классических алгоритмов. Вместо этого он предложил идею квантового симулятора, сегодня называемого квантовым компьютером. Один из учеников Фейнмана увидел в этой идее большой потенциал для проверки многомировой интерпретации Эверетта, и в 1985 г. разработал первый квантовый алгоритм. Другой ученик Фейнмана отнёсся к его идее скептически и продолжил изучение клеточных автоматов. Первого ученика звали Дэвид Дойч, второго – Стивен Вольфрам.

Стивен Вольфрам и его физический проект

Стивен Вольфрам был вундеркиндом из богатой английской семьи. Он публиковал статьи по квантовой теории поля с 15 лет, в 1979 г. он поступил в Калифорнийский технологический институт и уже через год получил степень доктора философии по физике элементарных частиц. В 21 год он стал самым молодым получателем стипендии Макартура, в основном по рекомендации Ричарда Фейнмана, который сказал: «я не знаю никого в этой области, кто обладал бы таким широким кругозором, как доктор Вольфрам». В 1983 г. Вольфрам ушел в Школу естественных наук Института перспективных исследований в Принстоне и занялся моделированием турбулентных потоков жидкости на Connection Machine вместе с Фейнманом. В 1986 г. Вольфрам перешёл в Иллинойсский университет, где открыл Центр исследований сложных систем (CCSR). Год спустя он ушёл из науки, основал компанию Wolfram Research и приступил к разработке компьютерного приложения Mathematica, которое было выпущено в 1988 г. и стало основным источником его прибыли.

В 2002 г., после десяти лет работы, Вольфрам самостоятельно опубликовал 1280-страничный трактат A New Kind of Science («Наука нового типа»), в котором изложил основы своей методологии и сформулировал принцип вычислительной эквивалентности, согласно которому «очень простые правила производят очень сложное поведение» и «почти все процессы, которые не являются очевидно простыми, могут рассматриваться как вычисления эквивалентной сложности». Хотя Вольфрам и называет этот принцип «единственным самым удивительным научным открытием, которое я когда-либо сделал», на самом деле он тесно связан с эффектом бабочки в теории хаоса. Поскольку крайне простые системы могут производить вычисления абсолютно любой сложности, всё на свете может быть вычислено одной простой машиной – реализацией клеточного автомата. Любые физические объекты, начиная с элементарных частиц и заканчивая галактиками – это просто шаблоны в клеточном автомате, подобные планерам в игре «Жизнь». Какие-то из этих фигур стабильны, другие долго эволюционируют или зацикливаются, а третьи почти сразу рассыпаются. Аналогично у нас есть стабильные долгоживущие частицы, есть быстро распадающиеся, а есть ненаблюдаемые частицы вроде кварков, которые существуют только как часть более сложной структуры – адрона.

В 80-е гг. Стивен Вольфрам классифицировал 256 возможных правил для одномерных клеточных автоматов, разделив их на четыре класса: 1) правила, которые быстро создают однородные стабильные конфигурации из нулей или единиц; 2) правила, которые в зависимости от начальных конфигураций создают однородный конечный узор или цикл между конечными узорами; 3) правила, которые создают и сохраняют псевдослучайные конфигурации, хотя могут присутствовать и некоторые регулярные паттерны; 4) правила, создающие устойчивые, регулярные, но непериодические паттерны (солитоны), взаимодействующие сложным и непредсказуемым образом. К 4-му классу относится правило 110, которое до сих пор считается простейшей вычислительной моделью из всех известных. В 2004 г. научный сотрудник Вольфрама Мэтью Кук доказал, что правило 110 является Тьюринг-полным, т.е. с его помощью можно смоделировать любую машину Тьюринга.

Так если простые вычислительные правила – по сути элементарные компьютерные программы – могут создавать замысловатые конструкции с непредсказуемым самоорганизующимся поведением, может и вся наша Вселенная является такой программой? Для Вольфрама это само собой разумеется: «для нас естественно думать о последовательных состояниях мира как о вычисляемых одно из последнего путём последовательного применения некоторого вычислительного правила». Соответственно, «…под законами физики, какими мы их знаем сегодня, может быть, лежит простая программа, из которой возникают все известные законы…». Написана эта программа на самом низкоуровневом машинном языке, но если разгадать её код, можно будет воспроизвести всю известную физику.

Книга «Наука нового типа» стала бестселлером, несмотря на критические отзывы со стороны учёных. В 2009 г. фирма Wolfram Research представила базу знаний Wolfram Alpha – систему ответов с большой библиотекой алгоритмов и обработкой естественного языка. В октябре 2019 г. Вольфрам вместе с молодыми физиками Джонатаном Горардом и Максом Пискуновым запустил проект Wolfram Physics, целью которого является поиск самого короткого правила (алгоритма), рекурсивным применением которого можно полностью смоделировать нашу Вселенную. В 2020 г. Вольфрам объявил о возможном «пути к фундаментальной теории физики» и опубликовал вышеупомянутый 448-страничный документ, а в 2022 г. запустил исследовательский институт Wolfram Institute for Computational Foundations of Science. Все материалы проекта находятся в открытом доступе и обновляются в реальном времени на сайте wolframphysics.org.

Вольфрам прямо не называет свою вычислительную модель теорией всего, но преподносит её как «парадигму», «фреймворк» и «вычислительные инструменты» для всей современной науки. Он объясняет через клеточные автоматы второй закон термодинамики, гидродинамику, специальную и общую теорию относительности, квантовую механику, биологическую эволюцию, морфогенез, искусственный интеллект, эффективные алгоритмы и NP-полноту, криптографию и псевдослучайность, сжатие данных, статистическую проверку гипотез, теорему Гёделя, аксиоматическую теорию множеств и тезис Чёрча-Тьюринга, а также философские вопросы о пределах познания, свободе воли и трудной проблеме сознания. Если этого мало, Вольфрам осторожно предполагает, что в его моделях «есть намёки» на теорию струн, голографический принцип, теорию причинных множеств, петлевую квантовую гравитацию, теорию твисторов, геометрическую теорию групп, теорию категорий высокого порядка, некоммутативную геометрию и геометрическую теорию сложности.

Математика и методология Вольфрама отличается от всего, что до сих пор было известно физикам. Традиционно под физической теорией понимали набор уравнений, которые позволяют количественно описать физическую систему и предсказывать её эволюцию. Правда, остаётся непонятным, каким образом решаются эти уравнения, когда мир переходит из одного состояния в другое. Поэтому Вольфрам использует вместо уравнений простые компьютерные программы (правила), а вместо чисел – причинно-следственные связи, и передаёт идеи не формальными символами, а графическими изображениями. Простая программа, согласно Вольфраму, должна удовлетворять следующим требованиям:

• Её работу можно полностью объяснить с помощью простого графического изображения.

• Её можно полностью объяснить несколькими предложениями естественного языка.

• Её можно реализовать на компьютерном языке в несколько строчек кода.

• Число её возможных вариаций достаточно мало для того, чтобы всех их можно было найти вычислительным образом.

Вычислительная неприводимость

Если вы уже прониклись идеями Вольфрама, сразу вынужден вас разочаровать. Команде Wolfram Physics не удалось найти то самое правило (алгоритм), которое даёт три пространственных измерения, конкретную скорость расширения Вселенной, актуальные значения фундаментальных констант, и т.д. В чём же проблема? Основным препятствием на пути к воссозданию исходного кода Вселенной Стивен Вольфрам считает вычислительную неприводимость: даже если известны начальные условия и точное правило, по которому работает система, вы не можете понять, как эта система работает, и предсказать результат её эволюции без выполнения каждого шага вычисления. Эта идея, предложенная Стивеном Вольфрамом в книге «Наука нового типа», имеет ключевое значение для понимания его последующих работ.

Действительно, в природе только самые простые системы ведут себя понятно и предсказуемо, однако более сложные системы вычислительно неприводимы и непредсказуемы: производимые ими вычисления невозможно упростить и сократить, единственный способ их смоделировать – это проследить каждый шаг вычисления. Принцип вычислительной эквивалентности подразумевает, что эти системы вычислительно столь же мощны, как и любой универсальный компьютер, а систем большей мощности в нашей Вселенной нет. Универсальный компьютер можно заставить симулировать любую вычислительную систему, включая самого себя. Универсальные правила для клеточных автоматов также можно использовать для симуляции любых других правил, но не существует гипервычислительной машины, способной сделать это эффективнее.

Второй фактор, мешающий нам найти то самое правило Вселенной – это наша вычислительная ограниченность. Как наблюдатели, мы сами является частью Вселенной и встроены в её структуру, поэтому воспринимаем только близлежащую её область и не можем охватить систему целиком. В качестве аналогии Вольфрам приводит термодинамику газа, которая является приближённой статистической моделью его молекулярной динамики. Помянём демона Максвелла, с которым мы расправились в статье «Информация об информации». Чтобы отследить траектории и столкновения каждой молекулы газа, демон должен производить сложные вычисления и запоминать много информации, что приводит к увеличению его энтропии. Но вычислительные ресурсы мозга не безграничны, поэтому приходится использовать усреднённые данные вроде температуры и давления газа. Точно так же теория относительности и квантовая механика являются приближёнными моделями для описания «атомов» пространства и сложных взаимоотношений между ними.

Почти в любом случае, когда поведение системы не очевидно простое, не существует алгоритма расчёта состояния системы после определенного количества итераций с вычислительной сложностью меньшей, чем вычислительная сложность осуществления всех этих итераций. Эта невозможность «обогнать» вычисление тесно связана с проблемой остановки и теоремой Гёделя о неполноте. Кроме того, понятие вычислительной несократимости пересекается с колмогоровской сложностью и энтропией по Шеннону, о которых мы также писали в статье «Информация об информации». Вычислительная неприводимость, по словам Вольфрама, является «младшей сестрой неразрешимости» — невозможности алгоритмическим способом получить ответ «да/нет» на вопрос о доказуемости того или иного математического утверждения, выполнимости той или иной функции и завершимости той или иной программы. Согласно теореме Тьюринга, главной особенностью универсального вычисления является то, что в принципе невозможно предсказать, остановится ли данное вычисление при определённых входных данных.

По мнению Вольфрама, неприводимость также лежит в основе закона неубывания энтропии и термодинамической стрелы времени. Она же ответственна за шифрование начальных условий Вселенной. К счастью, среди вычислительной неприводимости неизбежно есть слои вычислительной приводимости, три из которых соответствуют общей теории относительности, квантовой механике и статистической механике.

Пространственные гиперграфы и «выведение» теории относительности

Основным инструментом в методологии Стивена Вольфрама являются графы – математические структуры, обозначающие абстрактные связи (рёбра) между абстрактными элементами (вершинами). Гиперграф – обобщение графа, в котором одним гиперребром можно соединить более двух вершин, т.е. любые подмножества множества вершин. Правила – это короткие вычислительные операции над графами, устанавливающие порядок их обновления. Вселенная – один большой гиперграф, вычисляющий сам себя многократным применением одного и того же простого правила. По сути это усложнённая многомерная версия клеточного автомата. Вершины (точки) и соединяющие их рёбра (линии) – это события и причинно-следственные отношения между ними. В основе своей гиперграфы дискретны, но начиная с определённого масштаба они выглядят как непрерывные поверхности – подобно непрерывной водной глади, состоящей из дискретных молекул. Рекурсивное применение простых правил позволяет строить замысловатые фигуры, удивительно напоминающие реальные физические объекты, простейшие организмы и клеточные органеллы.

Предсказание результата применения данного правила к данному гиперграфу вычислительно неприводимо – чтобы узнать следующее состояние графа нужно пошагово рассчитать его. Но для наблюдателя, существующего внутри этого гиперграфа и ограниченного в своих вычислительных возможностях, это не представляется возможным. По мнению Вольфрама, пространство обозримой Вселенной представляет собой гиперграф, построенный примерно из 10⁴⁰⁰ точек (событий) за 10⁵⁰⁰ итераций одного и того же правила. Вся существующая материя тоже является частью этого гиперграфа, но для её описания необходимо в 10²⁰⁰ меньше ресурсов, чем на поддержку структуры самого пространства. Частицы – устойчивые эмерджентные структуры, локализованные в причинно-следственном гиперграфе, а не в пространстве-времени. Если в квантовой теории поля частицы движутся и взаимодействуют на фоне классического пространства-времени Минковского, то в теории Вольфрама они неразрывно встроены в сеть и соответствуют отпределённым её структурам, подобным глайдерам, кораблям, пожирателям и другим клеточным фигурам в игре «Жизнь». Такие структуры, состоящие из одного пространства, называются топологическими геонами. Вольфрам сравнивает их с вихрями в жидкостях или чёрными дырами в пространстве-времени, рассматривая как «топологические препятствия», которые не позволяют гиперграфу «легко распутываться».

Традиционной проблемой всех вычислительных моделей Вселенной было то, что они дискретны – любое вычисление происходит с определённым шагом во времени и пространстве, согласно алгоритму или правилу обновления состояний. Но существование элементарных «пикселей» или «вокселей» пространства-времени противоречит теории относительности Эйнштейна, согласно которой длины объектов и объёмы пространства зависят от системы отсчёта, в которой находится наблюдатель. Из-за лоренцева сокращения длины покоящийся и движущийся наблюдатели не смогут договориться о размерах объектов, а если разогнаться до околосветовой скорости, неподвижные объекты сожмутся для вас настолько, что станут меньше «пикселей» пространства. Наблюдения не подтверждают никаких нарушений лоренц-симметрии, малейшие отклонения от неё проявлялись бы в свойствах элементарных частиц.

Модель Вольфрама избегает нарушения лоренц-инвариантности тем, что использует нефизические причинно-следственные связи, у которых нет длины. Расположение точек гиперграфа, их нумерация и длина рёбер не имеют значения – важно только, что с чем соединено и в каком порядке, в пределах одного отношения. Такой гиперграф называется ориентированным: порядок соединения точек в гиперребре обозначается на нём стрелками. Правила перезаписи участков абстрактного гиперграфа не содержат никаких упоминаний геометрии или трёхмерного пространства. Гиперграф может иметь дробную размерность (как фрактал), поэтому для описание искривления такого пространства нужна особая математика – обобщение матанализа вроде геометрической теории групп.

По мнению Вольфрама, представление Эйнштейном времени как четвёртого измерения в едином пространственно-временном континууме – крупнейшая ошибка физики XX века, сбившая науку с правильного пути. Время принципиально отлично от пространства и соответствует вычислительному процессу последовательного итерационного применения правил, которые преобразуют структуру гиперграфа. «На самом низком уровне состояние вселенной представлено гиперграфом, который фиксирует то, что можно рассматривать как «пространственные отношения» между дискретными «атомами пространства». Время тогда соответствует прогрессивному переписыванию этого гиперграфа»

Фактически это возвращение к абсолютному ньютоновскому времени – замена «временной координаты» на «счётчик вычислительных шагов». Течение времени соответствует необратимому и неприводимому вычислительному процессу обновления пространственного гиперграфа. В дискретном пространстве невозможно плавное перемещение объекта из одного места в другое путём постепенного посещения всех мест между ними, но для наблюдателей, которые встроены в гиперграф и обновляются вместе с ним, пространство и время кажутся непрерывными. «Мы ощущаем время из-за взаимодействия между нашей вычислительной ограниченностью как наблюдателей и вычислительной неприводимостью базовых процессов во вселенной». Эти факторы не дают нам «воспринимать всё будущее одним глотком», и мы вынуждены следовать линейной цепочке вычислительных шагов.

Итак, теперь мы можем резюмировать, каким образом из простейших правил, задающих структуру пространственно-временного гиперграфа, можно вывести все наши знания о пространстве, времени, гравитации и других физических явлениях:

• пространство с различным количеством измерений – это поверхность гиперграфа;

• время – это дискретный процесс обновления гиперграфа, то есть последовательное применение правил, изменяющих его структуру;

• геодезические линии (искривление пространства-времени в ОТО) – это кратчайшие расстояния между точками гиперграфа;

• энергия – это поток причинно-следственных рёбер через пространственные гиперповерхности;

• импульс – это поток причинно-следственных рёбер через временные гиперповерхности;

• скорость света как предельная скорость передачи информации соответствует максимальному значению угла светового конуса (45°) и максимальной скорости обновления гиперграфа;

• элементарная частица – это локально стабильная структура гиперграфа, к которой сходятся причинно-следственные связи, определяющие её энергию и импульс;

• виртуальные частицы вакуума – это элементы гиперграфа, поддерживающие саму структуру пространства-времени без необходимости введения космологического лямбда-члена (тёмной энергии);

• горизонт событий чёрной дыры – это точка, где причинно-следственные связи расщепляются и больше не пересекаются;

• чёрная дыра – «отломавшаяся» часть гиперграфа;

• сингулярность – это точка, в которую сходится множество причинно-следственных связей гиперграфа;

• тёмная материя – это скопления гипотетических олигонов – очень маленьких и лёгких частиц, которые могли в большом количестве образоваться в ранней Вселенной, не вступающих ни в какое взаимодействие, кроме гравитационного.

Причинно-следственная инвариантность, многоканальные графы в пространстве ветвлений и «выведение» квантовой механики

Мы выяснили, что пространство в планковских масштабах – это классический дискретный гиперграф, лишённый квантовых свойств. Классическая физика основана на детерминизме – обладая полной информацией о настоящем, можно пошагово воссоздать всё прошлое и предсказать всё будущее системы. Но в квантовой физике каждому состоянию системы соответствуют множество совместимых с ним прошлых и будущих. Теорема Белла показала, что квантовая физика не может быть воспроизведена с помощью классического алгоритма. Однако теория рекурсивно самовычисляющей Вселенной обходит этот запрет.

Стивен Вольфрам – не первый, кто пытается построить дискретную детерминированную модель квантовой механики на основе клеточных автоматов. В 2016 г. голландский физик Герард ‘т Хоофт опубликовал монографию «Клеточно-автоматная интерпретация квантовой механики», в которой он также использует теорию причинных множеств и отстаивает супердетерминизм – теорию, согласно которой квантовые суперпозиции и случайности обусловлены исключительно нашим незнанием реальных скрытых параметров, на самом же деле Вселенная всегда находится в определённом онтологическом состоянии, а все результаты экспериментов и решения экспериментаторов предопределены ещё в первые секунды Большого взрыва. Поскольку клеточные автоматы являются детерминированными классическими компьютерами, можно подумать, что теория Вольфрама тоже является разновидностью супердетерминизма с локальными скрытыми параметрами. Но это не так.

Дело в том, что Вселенная Вольфрама является многоканальной (недетерминированной) машиной Тьюринга, осуществляющей мультивычисление. Пространственный гиперграф последовательно переписывается в соответствии с определённым правилом, но в нём есть много мест, где можно применить это правило. Разный порядок применения одного и того же правила даёт множество вычислительных веток (историй). Для рассмотрения всех возможных вычислительных историй Вольфрам вводит новую структуру – многоканальный граф. Его рёбра – это уже знакомые нам причинно-следственные связи, а точки (узлы) представляют разные состояния пространственного гиперграфа. Многоканальный граф ветвится в пространстве ветвлений, которое соответствует пространству квантовых состояний. Геометрия многоканального графа сходится к геометрии комплексного проективного гильбертова пространства в пределе континуума. Полный срез многоканального графа в пространстве ветвлений – аналог унитарной эволюции в квантовой механике. Фаза квантовой амплитуды – это координата в пространстве ветвлений, тогда как величина амплитуды связана с комбинаторным подсчётом возможных путей в многоканальном графе. «Мы показываем, что эволюция результирующей многоканальной системы, которая эффективно содержит все возможные ветви истории эволюции (соответствующие всем возможным порядкам обновления гиперграфа), аналогична эволюции линейной суперпозиции чистых квантовых собственных состояний» — пишет Джонатан Горард.

В многоканальном графе есть как разветвления историй, так и слияния – когда разный порядок применения одного и того же правила, согласно теореме Чёрча-Россера, даёт в итоге одинаковое состояние пространственного гиперграфа. Получается своего рода «ветвление наоборот», т.е. древо многоканального графа разрастается как вперёд, так и назад во времени. Вольфрам называет это свойство причинно-следственной инвариантностью: один и тот же гиперграф можно получить разными способами, поэтому проследить историческую последовательность обновлений становится невозможно – информация о том, по какой ветви многоканального графа шло вычисление, стирается. Каждая отдельная история полностью детерминирована, но при их слиянии невозможно узнать, по какому пути эволюции следовал гиперграф. Детерминированная эволюция запрещает правила обновления, которые в зависимости от порядка их применения могут давать неэквивалентные состояния гиперграфа. Есть только причинно инвариантные правила, порядок применения которых не влияет на итоговое состояние гиперграфа. Это можно сравнить с формулой «от перемены мест слагаемых сумма не меняется» и с принципом, известным каждому программисту: если есть правило, которое что-то делает, всегда есть другое правило, которое может это отменить. Слияния происходят при квантовом измерении, когда наблюдатель определяет состояния как макроскопически неразличимые. По мнению Вольфрама, причинно-следственная инвариантность имеет решающее значение в деле объединения теории относительности и квантовой механики.

Многоканальный граф и геометрия пространства ветвлений предоставляют карту запутанности между квантовыми состояниями, объясняя тем самым кажущуюся нелокальность и нарушение неравенства Белла. Причинно-следственные связи есть не только между состояниями на одной ветви многоканального графа, но и между структурами на разных его ветвях. Эти нити в пространстве ветвлений соответствуют сильной ЭПР-запутанности двух частиц. В теории Вольфрама нет классических скрытых параметров, дополняющих квантовую волновую функцию. Он считает саму волновую функцию (вектор состояния) не более чем полезным инструментом для описания некоторых эмерджентных явлений, производных от низкоуровневых процессов обновления гиперграфа. В роли скрытых параметров выступает сложная структура множества вычислительных историй, которые объединяются и перекрываются, чтобы сформировать то, что мы воспринимаем как случайный квантовый результат. Возможность предсказания этого результата через пространство ветвлений ограничена мультивычислительной неприводимостью – не сложностью выполнения конкретного пути вычислений, а сложностью увидеть, как много запутанных путей взаимодействуют. Впрочем, неспособность наблюдателя знать полное состояние гиперграфа субъективно ничем не отличается от случайности.

Согласно «интерпретации завершения» (Completion Interpretation of Quantum Mechanics) Джонатана Горарда, процедуру квантового измерения можно описать алгоритмом завершения Кнута-Бендикса. Этот алгоритм используется для упрощения систем соотношений между элементами в математических структурах, преобразуя набор правил так, чтобы они не повторялись и не противоречили друг другу. Наблюдатель выбирает квантовую систему отсчёта, определяющую пучок (суперпозицию) вычислительных нитей истории, которые могут быть соединены, и эффективно сводит их к одной нити, когерентно представляющей результат измерения. Без объединения этих ветвей в единую нить опыта и установления эквивалентности через пространство ветвлений между состояниями на «грубозернистом» уровне мы не можем говорить о том, что произошло, а только о том, что может происходить. Это будет не вычисление, а мультивычисление. Интерференция рассматривается как побочный продукт процедуры завершения Кнута-Бендикса для многоканальных графов: частицы, находящиеся на противоположных концах пространства ветвлений, будут деструктивно интерферировать, а находящиеся рядом – конструктивно интерферировать. Энтропия – это мера количества возможных конфигураций ветвящегося графа, согласующихся с определённым крупнозернистым измерением.

Компьютерные модели проекта Wolfram Physics дают некоторые подсказки, как можно согласовать общую теорию относительности с квантовой механикой. Так, релятивистская «заморозка» времени на горизонте событий чёрной дыры напоминает Вольфраму квантовый эффект Зенона (если многократно измерять систему достаточно быстро, она не изменится). Процесс квантового измерения, который на многоканальном графе выглядит как «заморозка» времени для одного конкретного состояния из суперпозиции возможных, вызывающая декогеренцию путём вовлечения всё большего количества причинно-следственных связей. Действительно, для поддержания кубита в определённом состоянии нужно изолировать его в пространстве ветвлений так же, как частицы оказываются изолированы в физическом пространстве при пересечении горизонта событий. Ещё Вольфрам предполагает, что статистика Ферми-Дирака может быть связана с многоканальными графами, где ветви не сливаются, а статистика Бозе-Эйнштейна – наоборот, с теми, где мы видим слияние всех ветвей. В таком случае спинорные поля фермионов соответствуют ориентированным гиперграфам, а векторные поля бозонов – неориентированным гиперграфам.

Самым красивым следствием своей модели Вольфрам считает соответствие между движением в пространстве и эволюцией квантовых амплитуд. Свойства искривлённого пространства ветвлений подобны кривизне физического пространства в ОТО: как присутствие энергии-массы изгибает пространство-время и порождает гравитацию, так и события обновления искривляют геодезические линии, по которым происходит движение в пространстве ветвлений, поворачивая их на определённый угол. Этот поворот фазы задаётся в комплексных числах интегралом по траекториям, а величина, называемая действием, является релятивистским аналогом энергии и соответствует потоку причинно-следственных рёбер, которые определяют скорость поворота геодезических линий. Так уравнения Эйнштейна волшебным образом превращаются в фейнмановский интеграл по траекториям, и оказывается, что квантовая механика в пространстве ветвлений – то же самое, что и теория относительности в физическом пространстве.

Вольфрам добавляет к максимальной скорости перемещения в физическом пространстве c (скорости света) ещё одну константу ζ (дзета) – максимальную скорость квантового запутывания в пространстве ветвлений. Она равна запутыванию примерно 10¹⁰² новых квантовых состояний в секунду, или преобразованию энергии порядка 10⁵ солнечных масс в секунду, что эквивалентно энергии столкновения двух сверхмассивных чёрных дыр. В связи с этим Вольфрам предсказывает наличие у чёрной дыры горизонта запутанности в пространстве ветвлений, который не совпадает с горизонтом событий в физическом пространстве. Информация, оказавшаяся под горизонтом запутанности, «замораживается» на поверхности. Оба горизонта отсекают часть причинно-следственного гиперграфа, но один делает это в физическом пространстве, другой – в пространстве ветвлений. Подобно тому, как при пересечении горизонта событий наблюдатель бесконечно удлиняется (спагеттифицируется) под действием приливных сил, при пересечении горизонта запутанности он удлиняется в пространстве ветвлений, что не позволяет ему провести квантовое измерение и сформировать классическую картину мира, чтобы понять, упало что-то в чёрную дыру или нет.

Отсюда Вольфрам выводит решение информационного парадокса чёрных дыр, совпадающее с выводами, полученными в рамках голографического принципа и AdS/CFT- дуальности. Объект, падающий в чёрную дыру, с точки зрения внешнего наблюдателя в многоканальном графе будет казаться «застывшим» на горизонте запутанности из-за квантового эффекта Зенона и никогда не приблизится к истинному причинному горизонту событий. Излучение Хокинга возникает как следствие неконвергентных пар ветвей в многоканальном графе и испускается из горизонта запутанности, а не из причинного горизонта событий. Поэтому частицы излучения чёрной дыры могут быть идеально коррелированы с информацией, содержащейся в падающем объекте, без нарушения специальной теории относительности – никакая информация никогда не пересекает пространственно-временной горизонт событий.

Вольфрам не верит в квантовое превосходство, по крайней мере на формальном уровне, и связывает ограничение эффективности квантовых вычислений со своей константой ζ. Он рассматривает квантовый компьютер как многоканальную машину Тьюринга, осуществляющую параллельное вычисление вдоль всех возможных ветвей многоканального графа, а затем связывающую эти ветви вместе, чтобы дать определённый ответ. Классические машины Тьюринга вычисляют по одному пути многоканального графа, используя детерминированное правило для выбора ветвей, по которым следовать; недетерминированные машины Тьюринга также вычисляют по одному пути, но используя недетерминированное правило для выбора последовательности ветвей; а квантовые машины Тьюринга вычисляют по всему многоканальному графу, т. е. по суперпозиции всех возможных путей. Непрерывный спектр состояний кубита выводится из дискретной вычислительной модели как эффективное приближение – результат взаимодействия разных вычислительных историй. Вычислительные правила, управляющие гиперграфами, аналогичны унитарным преобразованиям в квантовой механике, что позволяет моделировать квантовые алгоритмы.

Рулиада, пространство правил и физикализация метаматематики

До сих пор мы следовали предположению, что существует одно единственное правило обновления пространственного гиперграфа, которое применяется разными способами и создаёт многоканальный граф. Однако из-за вычислительной неприводимости и нашей ограниченности как наблюдателей, встроенных в гиперграф, мы никогда не сможем «дойти до сути физики» и найти то самое правило. Даже если его получится обнаружить в ходе случайного перебора, мы не сможем объяснить, почему Вселенная задаётся именно этим конкретным правилом, а не каким-нибудь другим. Есть не одно, а целый набор правил, которые дают на выходе наблюдаемое состояние Вселенной и согласуются со всеми результатами экспериментов. И здесь Стивен Вольфрам задаёт вопрос: а что, если Вселенная одновременно выполняет все возможные правила и в результате порождает все возможные вычислительные истории? На первый взгляд, тогда мы не смогли бы сказать о Вселенной ничего определённого. Вольфрам не согласен с этим.

Каждый участок пространственного гиперграфа обновляется в соответствии с разными вычислительными правилами, но в силу причинно-следственной инвариантности разные правила приводят к идентичным состояниям гиперграфа, соединяя параллельные вычислительные истории. Применяя к определённому состоянию гиперграфа все возможные правила, мы получим множество новых различных состояний. А применяя все возможные правила к различным состояниям гиперграфа, мы можем получить одно и то же новое состояние. Многоканальный граф всех возможных состояний вселенной, задаваемых всеми возможными правилами, Стивен Вольфрам называет рулиадой. Рулиада – запутанный предел всех возможных вычислений (формальных процессов), абстракций и обобщений. Фактически это полный репертуар универсальной машины Тьюринга, реализованный физически. Получается, что мы живём в мире идей и математических абстракций, а наблюдаемую физическую реальность Вольфрам считает иллюзорной, как это делают последователи адвайта-веданты и буддизма.

Рулиада включает в себя всё, что может быть вычислено конечным множеством непротиворечивых правил, лежащих в её основе. И не нужно никакого компьютера, который выполнял бы эти алгоритмы: каждая программа существует сама по себе как абстракция в мире идей, просто потому, что может существовать. Большинство правил не дают ничего интересного, но есть исключения вроде правила 30, порождающего сложный паттерн. Стивен Вольфрам выбирает подобные правила и составляет на своём сайте «реестр замечательных моделей вселенных». Рулиада симметрична между «прямыми» и «обратными» правилами, то есть ветвится в обе стороны в пространстве правил, движение в котором означает переход с одного правила на другое. Световым конусам в физическом пространстве и конусам запутывания в пространстве ветвлений соответствуют трансляционные конусы (конусы эмуляции) в пространстве правил. Ни одно правило не может моделировать другое бесконечно быстро: есть максимальная скорость трансляции или движения в пространстве правил ρ, аналогичная скорости света c в физическом пространстве или максимальной скорости запутывания ζ в пространстве ветвлений. В некотором смысле ρ является конечной скоростью работы процессора нашей Вселенной. Она равна длине программы, разделённой на время её выполнения. Если измерять ρ в единицах «токенов Wolfram Language в секунду», константа равна порядка 10⁴⁵⁰ WLT/сек.

Так если всё, что мы когда-либо могли переживать или воображать, является частью рулиады, почему же мы наблюдаем одно определённое состояние Вселенной в определённый момент времени, а не все сразу? Всё из-за той же вычислительной неприводимости и вычислительной ограниченности наблюдателя. Мы не можем охватить своим разумом всю рулиаду и посмотреть на неё со стороны вне времени, поэтому вынуждены наблюдать только один срез рулиады – выборку состояний в пространстве правил, соответствующих нашему способу восприятия и понимания Вселенной. Изменяя систему отсчёта в рулиаде, мы переводим свой опыт с одного формального языка описания на другой (например, с языка математических формул на любой язык программирования), что возможно благодаря вычислительной универсальности. И если мы хотим выстроить последовательный поток связного опыта, мы непременно придём к выводу о действии в мире законов теории относительности и квантовой механики. Но по мере роста наших знаний и технологий мы можем выбрать другой срез рулиады и получить другую, более общую теорию всего. Вольфрам сравнивает это с путешествием между вселенными:

«Первое впечатление может быть таким, что рулиада фактически содержит множество возможных «параллельных вселенных», и что мы выбрали себе в одну из них, возможно, вследствие наших особых характеристик. Но на самом деле рулиада не о «параллельных вселенных», она о вселенных, которые запутаны на самом тонком уровне. И важным следствием этого является то, что это означает, что мы не «застряли в определённой параллельной вселенной». Вместо этого мы можем ожидать, что каким-то образом «изменяя нашу точку зрения», мы можем фактически оказаться в «другой вселенной»

Если «носителями движения» в физическом пространстве являются частицы, а в пространстве ветвлений – макроскопические объекты, то в пространстве правил им соответствуют концепции, аналогии и синтаксические структуры. Двигаясь в пространстве правил, можно получить другое описание и другие эффективные законы для Вселенной. В целом рулиада содержит всевозможные «дикие» и вычислительно неприводимые структуры, но та её часть, которая связана с нами как с наблюдателями, имеет определенную простоту или вычислительную приводимость: по мере того, как мы развиваемся во времени или движемся в пространстве, мы каким-то образом сохраняем свою идентичность.

Рулиада чем-то напоминает Конечный ансамбль Макса Тегмарка как совокупность всех возможных математических структур. И Вольфрам, и Тегмарк считают, что физическая реальность не просто описывается математикой, а буквально является математикой. Но Тегмарк делает акцент на логической самосогласованности математических объектов, а Вольфрам – на их вычислимости. Если «атомы» пространства в узлах гиперграфов заменить абстрактными математическими элементами, которые Вольфрам называет «эмами» (по аналогии с генами и мемами), мы получим метаматематический предел всех возможных теорем, связывающий воедино основы физики и математики – рулиаду в абстрактном метаматематическом пространстве. Из набора правил (математических аксиом) сразу следуют все возможные теоремы и все возможные вычислительные пути доказательства их верности или ложности. Структуру из нескольких миллионов доказанных теорем Вольфрам называет «человеческой географией» метаматематического пространства, а внутреннюю геометрию рулиады – «физикализированной метаматематикой». Наши доказательства он сравнивает с эмерджентной гидродинамикой, допуская существование низкоуровневой «молекулярной динамики» — более детальных формальных выводов, т.е. автоматизированного доказательства теорем. Мы не можем полностью формализовать математику, потому что в её основе лежит «нечеловеческий машинный код», от которого 4 или 5 порядков величины до типичных формулировок, с которыми имеют дело люди.

Таким образом, Стивен Вольфрам пытается «физикализировать» метаматематику и эпистемологию, т.е. наделить статусом физического существования математическую структуру, «знающую» всё, что в принципе можно знать о Вселенной. Это напоминает попытку Рассела и Уайтхеда в «Принципах математики» решить вторую задачу Гильберта – систематизировать математику и автоматизировать доказательство её теорем. Теперь подобной системой является Wolfram Alpha, цель которой – «собрать как можно больше знаний и сделать их вычислимыми», чтобы выяснить, какие теоремы о конкретной структуре или системе являются «интересными» или «мощными». Вольфрама не смущает теорема Гёделя – он считает неполноту очередным проявлением вычислительной неприводимости, которая не даёт нам как наблюдателям формализовать всю математику.

А что находится за пределами рулиады? Принцип вычислительной эквивалентности предполагает существование только одного конечного класса эквивалентности для вычислений, соответствующего репертуару универсального компьютера, а физический тезис Чёрча-Тьюринга, также называемый тезисом Дойча-Вольфрама, запрещает гипервычисления в нашей вселенной. Однако Стивен Вольфрам допускает теоретическую возможность гипервычисления с оракулом для машины Тьюринга, которое за конечное число шагов даст результат из бесконечного числа шагов вычислительно неприводимого процесса. Такое гипервычисление не является частью нашей рулиады, но может входить в некую гиперрулиаду. Кроме того, ничто не мешает нам представить бесконечную иерархию более мощных гиперрулиад, только все они отделены от нас своего рода «горизонтом событий», не позволяющим чему-либо из любой гиперрулиады влиять на что-либо в обычной рулиаде. Мы никогда не сможем их понять, потому что сами являемся наблюдателями, встроенными в рулиаду. Впрочем, некоторое представление о гиперрулиадах можно получить, изучая гипорулиады – версии рулиады, в которых возможны только ограниченные уровни вычислений.

Теория наблюдателя

Определяя наблюдателя как дискретное гиперповерхностное расслоение многоканального эволюционного графа, Вольфрам не уточняет, является ли он разумным или сознательным агентом. Главное, что наблюдатель является частью многоканального графа и разветвляется вместе с ним, обладая протяжённостью в пространстве ветвлений. В каждый момент времени мы сделаны из разных «атомов» пространства и разных ветвей в многоканальном графе. Но как «ветвящийся мозг» воспринимает разветвлённую вселенную? Он производит особое вычисление, которое «уничтожает информацию», т.е. имеет много входящих состояний, но мало исходящих. Если нормальная эволюция гиперграфа постоянно создаёт новые ветви, то наблюдение их соединяет («эквивалентизирует») и помещает в конечную память наблюдателя. Соединять похожие состояния гиперграфа в одну ветвь могут любые макроскопические объекты, усиливающие сигнал и записывающие его в своём состоянии: измерительные приборы, органы чувств и наш мозг.

Для вычислительно ограниченного наблюдателя общая теория относительности возникает как совокупное описание физического пространства, а квантовая механика возникает как совокупное описание пространства ветвлений. Наблюдатель не может независимо отслеживать индивидуальную эволюцию отдельных атомов пространства, будучи сам частью этого пространства. А из-за мультивычислительной неприводимости он не может отследить весь разветвляющийся и сливающийся многоканальный граф, поэтому выбирает из него только одну вычислительную историю. Так же, как наблюдатель может объединить своё представление об отдельных молекулах или атомах, чтобы воспринимать их коллективное свойство вроде температуры и давления, так же он может выбрать квантовую систему отсчёта как нечто, имеющее определённое состояние в определённый момент времени, и вычислительно приводимый срез всей вычислительно неприводимой эволюции вселенной.

Почему же мы получаем один результат измерения, а не другой? Всё зависит от нашего местоположения в пространстве ветвлений. Оглядываясь назад, мы можем проследить, как мы попали на данную ветку. Но нет способа определить, на какой ветви окажется наш субъективный опыт в будущем, и узнать, каким будет результат измерения. Несмотря на то, что многоканальный граф полностью детерминирован, остаётся произвольность того, где находится наблюдатель в пространстве ветвлений. Нахождение в разных местах в пространстве ветвлений соответствует выбору разных базисов для квантовых состояний. Возможность движения наблюдателя в пространстве ветвлений и пространстве правил каким-то образом связана с нашей верой в свободу выбора базиса измерения в экспериментах, которые мы проводим. Будучи частью рулиады, наблюдатель полностью детерминирован структурой рулиады и своей историей в ней. Но мы можем «верить в свободу воли» как отражение того факта, что мы не знаем заранее, где мы будем находиться в рулиаде, — и даже если бы мы знали, вычислительная неприводимость помешала бы нам спрогнозировать собственное поведение. Мы приписываем свободную волю системе тогда, когда не можем легко делать прогнозы о поведении системы. Причина не в хаосе и квантовой случайности, а всё в той же вычислительной неприводимости: система с простыми и определенными правилами, такими как те, которые управляют нашими нейронами, может производить непредсказуемое поведение, свободное от очевидных правил.

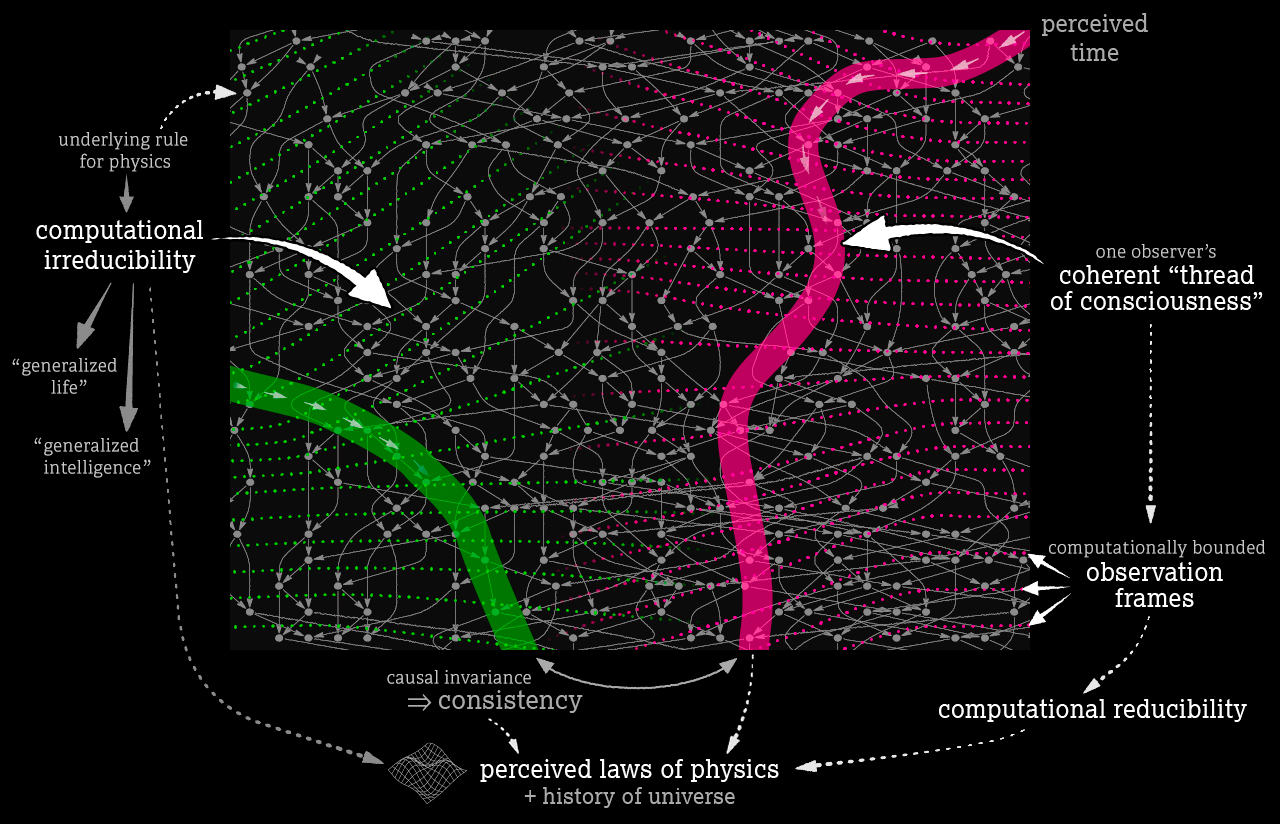
Сознание Стивен Вольфрам соотносит с вычислительной приводимостью, благодаря которой мы можем находить закономерности во всём, что не является вычислительно неприводимым. По его определению, сознание – поток сложных паттернов в гиперграфе, который сохраняют свою внутреннюю согласованность с течением времени. В переводе на человеческий язык это особенность нашего мозга, которая заставляет нас иметь связную нить опыта –  последовательный способ восприятия вселенной. Сознание наблюдателя объединяет различные истории в различных ветвях, интегрирует их в единую нить опыта и формирует определённые мысли об этом. Мы думаем, что во вселенной происходят определённые вещи, а не бесконечное древо ветвящихся историй, и верим, что являемся «стабильными наблюдателями» изменяющегося «внешнего мира». Если наблюдатель рассредоточится в пространстве ветвлений или пространстве правил, его опыт станет несвязным, а «я» — менее определённым.

Сравнивая мозг с нейросетями, Вольфрам отмечает, что первоначальная обработка сенсорной информации мозгом и другие процессы на уровне нейронов происходят параллельно, но на уровне мыслей и языка информация обрабатывается последовательно. Наш «внутренний опыт» следует только одной «нити истории», на которой мы можем работать вычислительно ограниченным образом, формировать определённые воспоминания и иметь определённые последовательности мыслей. Мы воспринимаем мир как состоящий из последовательности состояний пространства в последовательные моменты времени, потому что фотоны от большинства окружающих нас объектов достигают нас менее чем за микросекунду, а на осознание того, что мы увидели, мозгу требуются миллисекунды. Но если бы наш мозг был размером с планету, он не смог бы формировать связные мысли и последовательную нить опыта из-за ограниченности скорости света.

Почему же разные наблюдатели, проводящие разные измерения, воспринимают вселенную как работающую одинаково? Различные потоки сознания внутри гиперграфа приходят к одинаковым выводам относительно принципов работы Вселенной (существование причинно-следственных связей, времени, пространства, определённых законов физики) благодаря причинно-следственной инвариантности – какой бы срез пространства ветвлений мы ни выбрали, пространственный граф получается один и тот же, и какой бы срез пространства правил мы ни выбрали, наблюдаемая вселенная будет вести себя одинаково. Кроме того, разные наблюдатели приходят к согласию относительно объективной реальности, потому что находятся близко в многоканальном графе.

Также Вольфрам выводит из своей модели биологическую теорию эволюции, рассматривая организмы как вычислительные системы, которые развиваются согласно простым правилам. Правила соотносятся с генотипом, а результат их выполнения – с фенотипом. Дарвиновский естественный отбор – это адаптивная эволюция многоканальных машин Тьюринга (очевидно, репликаторов), которые пробуют случайные вариации (мутации), пока не находят путь через пространство правил (аналог адаптивного ландшафта) к большей приспособленности. Жизнь и разум – это просто разновидности вычислительной сложности. Существует бесконечное количество других возможных языков описания, которые могут привести к описаниям реальности, которые будут казаться связными внутри самих себя, но которые покажутся нам соответствующими совершенно бессвязным и бессмысленным аспектам нашей вселенной. Но иной разум может воспринимать иной срез гиперграфа, соответствующий иной системе отсчёта в пространстве правил, и тем самым получать реальность с другой физикой.

Многомировая интерпретация против теории Вольфрама

Ветвление многоканального графа на разные вычислительные истории очень напоминает ветвление реальности в многомировой интерпретации квантовой механики. Отсюда возникает вопрос: как соотносятся теории Вольфрама и Эверетта? Теория Вольфрама однозначно является теорией мультивселенной, но вычислительные истории, или ветви многоканального графа – это не совсем параллельные миры в эвереттовском смысле. Мультивёрс Эверетта представляет собой квантовую суперпозицию параллельных миров и составляющих их частиц, а многоканальный граф – скорее суперпозицию различных геометрий пространства-времени. Кроме того, в интерпретации Эверетта параллельные миры расходятся навсегда, а модель Вольфрама предполагает возможность пересечения вычислительных историй. Если у Эверетта при каждом измерении происходит расщепление миров, то у Вольфрама это наоборот соединение множества вычислительных историй в одну.

Джонатан Горард на вопрос о соотношении модели Вольфрама с многомировой интерпретацией отвечает так:

«Простейший вариант (эвереттовской) многомировой интерпретации квантовой механики, в которой нет эффективной интерференции между отдельными ветвями истории, можно рассматривать как соответствующий особому случаю многоканальной эволюции, в которой нет схождения пар ветвей (т. е. есть только расхождение пар ветвей), и в которой наблюдатель следует только одной многоканальной ветви. Полная версия нашей модели с конвергенцией пар ветвей и процедурами завершения, налагаемыми измерением (как подробно описано в вопросе об интерференции), может поэтому рассматриваться как соответствующая версии варианта многомировой интерпретации Дойча, в которой ветвям истории разрешено интерферировать»

То есть Мультивёрс Эверетта – частный случай, если выделить из многоканального графа ветвящееся древо следствий применения одного правила. А в общем случае реальность формируется в результате пересечения множества вычислительных процессов, что по мнению Горарда напоминает интерпретацию многих интерферирующих миров Дэвида Дойча. Действительно, трактовка двухщелевого эксперимента у Дойча и Вольфрама аналогичная: в одной многоканальной ветви фотон проходит через одну щель, в другой многоканальной ветви фотон проходит через другую щель, а затем интерферирует сам с собой. Но дело в том, что у Дойча интерферируют и сливаются только слабоотличимые, когерентные миры – как параллельные траектории фотона в двухщелевом эксперименте или параллельные пути вычисления в квантовом компьютере. Если же эти миры становятся декогерентными, т.е. запутываются со средой и делают её также отличимой, воссоединить их уже практически невозможно. Хотя между ними и сохраняется слабая интерференция, сами по себе эти ветви уже не сольются в одну. Подробнее о том, почему некогерентная интерференция почти никогда не происходит, я объяснял в статье «Мистическая эвереттика Менского-Лебедева» — для макроскопических объектов это настолько маловероятно, что время ожидания сравнимо с временем возвращения Пуанкаре.

Также подходы Дойча и Вольфрама различаются в философском отношении: Дойч придерживается физического реализма многомировой интерпретации и утверждает, что вычислительные процессы производны от физики, а Вольфрам считает, что в основе физической реальности лежат абстрактные вычислительные модели. На мой взгляд, вычислительный подход Вольфрама ближе к интерпретации многих взаимодействующих миров (Many Interacting Worlds, MIW), в которой квантовые эффекты (интерференция и запутанность) объясняются взаимодействием классических детерминированных миров. В интерпретации многих взаимодействующих миров (MIW) нет понятия универсальной волновой функции, суперпозиции и неопределённости – в каждом отдельном мире всё происходит детерминированно по законам классической механики, а вероятности отражают лишь незнание наблюдателя, в каком мире он находится, и трактуются как результат распределения множества миров, в которых происходят различные исходы.

Дополнительную сложность создаёт рулиада с пространством правил. Если пространство ветвлений соответствует бесконечномерному гильбертову пространству квантовых состояний, то пространство правил – это что-то вроде пространства состояний для инфляционной мультивселенной или ландшафта теории струн. Текущему состоянию гиперграфа Вселенной соответствует множество правил (т.е. законов физики), которые действуют согласованно и приводят к этому состоянию разными вычислительными путями. Причинно-следственная инвариантность предполагает, что разные последовательности применения одного и того же правила в многоканальном графе и разные вычислительные правила в рулиаде приводят к эквивалентным конфигурациям гиперграфа. То есть Вольфрам не просто повторяет ошибку Менского, допуская «склейки» между параллельными способами применения одного правила, но и вводит «склейки» между результатами применения разных правил – по сути между параллельными вселенными с разной физикой. Правил в рулиаде может быть очень много, их древа накладываются друг на друга и сливаются, а вычислительные истории сложным образом переплетаются, формируя единую согласованную реальность, которую мы называем наблюдаемой вселенной.

Мне кажется, причина всей этой путаницы в том, что Вольфрам не видит или намеренно игнорирует разницу между квантовыми амплитудами и классическими вероятностями. В его теории ничего не говорится о декогеренции – процессе, который предшествует измерению и сопровождается ветвлением наблюдателя. Как я объяснял в статье «Квантовая информация  и законы сохранения», волновая функция с её амплитудами описывает когерентные квантовые системы в чистом состоянии, а матрица плотности применима также к некогерентным смешанным состояниям, когда наблюдаемые переменные уже приняли определённые значения, но они ещё не известны наблюдателю. Согласно многомировой интерпретации Дойча, суперпозиция неотличимых копий наблюдателя когерентная (квантовая), а суперпозиция отличимых копий – декогерентная (классическая). В первом случае неопределённость обусловлена многообразием в пределах неотличимости, во втором случае – незнанием наблюдателя, кем из своих копий и в какой вселенной он фактически находится. В параллельных мирах Эверетта слабоотличимые копии наблюдателя могут квантово интерферировать, в мирах с другой физикой – нет.

Если применять интерпретацию Эверетта как метатеорию ко всему множеству математически возможных миров, мы получим ту же рулиаду Вольфрама. Там действительно могут быть миры с разной физикой, неотличимые для наблюдателя. Можно представить себе миры, в которых действуют ньютоновская механика, бомовская механика, теории объективного коллапса, петлевая квантовая гравитация, клеточно-автоматный супердетерминизм – для любой более-менее развитой и непротиворечивой теории найдётся своя вселенная. Какая теория всего работает именно в нашей наблюдаемой вселенной, мы не знаем. Согласно Вольфраму, это незнание обусловлено причинно-следственной инвариантностью в многоканальном графе и вычислительной ограниченностью наблюдателя. Но согласно многомировой интерпретации, оно обусловлено неопределённостью самолокации в Мультивёрсе – наблюдатель фактически находится в одном определённом мире с определённой физикой, но не может сказать, в каком именно. Это банальное классическое невежество, а не результат взаимодействия миров с разной физикой. Следовательно, Вольфрам со своей рулиадой просто переизобрёл эпистемологию!

Что не так с теорией Вольфрама

Когда Стивен Вольфрам опубликовал в 2002 г. «Науку нового типа», у него сразу появилось немало сторонников и ещё большее число критиков. Отзывы были самые противоположные. Например, журнал Wired поместил Вольфрама на обложку и назвал «человеком, который взломал код всего», а физик Фримен Дайсон отреагировал на книгу так: «Существует традиция, когда ученые, приближаясь к старости, выдвигают грандиозные, невероятные теории. Вольфрам необычен тем, что делает это в свои 40». И второе пришествие Вольфрама в 2019 г. прошло точно так же. Как и следовало ожидать, учёные и на этот раз приняли его теорию в штыки.

Первой претензией к Вольфраму стало несоблюдение им формальностей и правил «научного этикета». Вольфрам изолировал себя от физического сообщества и отказался от публикации статей в научных журналах с анонимным рецензированием, ссылаясь на коррумпированность системы. Вместо этого он сразу представил общественности 448-страничный доклад с открытым исходным кодом, ожидая от физиков публичных комментариев. Большинство учёных просто его проигнорировали, на что Вольфрам заявил, что «заслуживает большего».

Я не считаю отсутствие признания аргументом против теории, автоматически относящим её к псевдонауке. В отличие от классических лжеучёных и фальсификаторов, Вольфрам хотя бы реагирует на замечания и корректирует ошибки. Но всё же наука – это коллективный процесс, включающий конструктивную критику, совместную проверку, поиск несоответствий и внесение улучшений. А Вольфрам позиционирует себя как гения-одиночку, который изобрёл теорию всего с нуля, не делая ни одной ссылки на работы предшественников и не полагаясь на мнения современников. Это вписывается в концепцию научных революций Томаса Куна, но не отражает реального механизма роста научного знания путём вариации и отбора лучших объяснений. У миллиардера достаточно ресурсов, чтобы собрать команду исследователей, разработать сайт с красивыми картинками и разрекламировать свою теорию в популярных СМИ, но это не даёт ему карт-бланш и не освобождает от стандартной процедуры рецензирования.

Переход на личности – тоже не лучший аргумент, но иногда полезно знать, с кем мы имеем дело. Стивен Вольфрам настолько нарциссичен, что ещё с 80-х гг. регистрирует каждый свой шаг и каждое действие на компьютере: в предисловии к «Науке нового типа» он отметил, что записал более 100 миллионов нажатий клавиш и 100 миль движений мыши. Всю его работу можно проследить по видеозаписям, выложенным в открытый доступ. В этой прозрачности есть определённый смысл, по крайней мере оцифровать личность Вольфрама будет проще, чем кого бы то ни было. Многие причуды гению можно и простить, если бы не склонность Вольфрама преувеличивать свои достижения. Он приписывает себе открытие Принципа вычислительной эквивалентности, согласно которому практически безграничная сложность может возникнуть из простых правил, но на самом деле об этом говорили ещё Алан Тьюринг и Джон фон Нейман. Аналогичное неуважение к авторскому праву Вольфрам проявляет и в отношении своих научных сотрудников. Так было с Мэтью Куком, на которого Вольфрам подал в суд за нарушение договора о неразглашении доказательства Тьюринг-полноты Правила 110 до тех пор, пока он не опубликует свою книгу. Недавно история повторилась с Джонатаном Горардом, который пожаловался в твиттере на то, что Вольфрам присваивает его работы.

Ещё одна претензия состоит в том, что Вольфрам создал типичную «теория чего угодно», не имеющую предсказательной силы и не фальсифицируемую. По словам Скотта Ааронсона, это «бесконечно гибкая философия», из которой можно вывести любую физическую модель. Вольфрам прямо говорит, что его идея не может быть опровергнута:

«Любое конкретное правило может быть доказано неверным, если оно не согласуется с наблюдениями, например, предсказывает частицы, которые не существуют. Но общая структура наших моделей является чем-то более общим и напрямую не поддаётся экспериментальной фальсификации. Вопрос о том, как фальсифицировать нашу структуру, похож на вопрос о том, как доказать, что вычисление не может быть моделью для физики. Очевидным ответом будет другая модель, более успешная в качестве фундаментальной теории физики, и доказательство, что она несовместима с моей»

Другими словами, вы можете доказать его неправоту, только придумав собственную теорию, которая будет работать лучше. Более того, по словам Вольфрама, если его теория не сможет воссоздать Стандартную модель, то последняя просто неверна. Но до сих пор команда Вольфрама не нашла в своей вычислительной модели структуры, соответствующие электрону, кваркам и другим частицам Стандартной модели, не говоря уже о выведении точных значений фундаментальных констант, непрерывных симметрий и уравнений КТП. Заявление, что «из чрезвычайно простой модели мы можем воспроизвести специальную теорию относительности, общую теорию относительности и основные результаты квантовой механики» не соответствует действительности – теория не даёт количественных предсказаний с точностью до десятков знаков после запятой, как это делает КТП. А все качественные результаты объясняются тем, что Вольфрам изначально их туда вставил и подогнал модель под известные физические факты. Джонатан Горард открыто признаёт, что «Мы просто подгоняем вещи. Но мы делаем это только для того, чтобы на самом деле пойти и провести систематизированный поиск» конкретных правил, которые определяют структуру нашей Вселенной. Ирония в том, что точных правил команда Вольфрама так и не нашла, а без них теория согласуется с любыми экспериментальными результатами.

Справедливости ради следует сказать, что в плане фальсифицируемости теория Вольфрама не уступает теории струн или петлевой квантовой гравитации. Модель уже даёт некоторые предсказания, но они либо технически непроверяемые, либо мягко говоря странные. Например, из теории следует, что мы расширяемся вместе с наблюдаемой вселенной, а «гранулы» пространства становятся всё меньше и меньше. Вселенная в начале была бесконечномерной и только позже «расслабилась» до трёхмерной. Тождественные фотоны с заданной энергией-импульсом и поляризацией могут иметь общую топологическую структуру, но различаться в деталях конфигурации многоканального графа. Кроме того, по оценке Вольфрама, «элементарная длина» составляет порядка 10^–93 м, радиус электрона – порядка 10^–81 м, «квант массы» в 10³⁶ раз меньше массы электрона, а элементарное время – порядка 10^–100 с. Всё это на много десятков порядков меньше планковских единиц и едва ли может быть проверено на практике.

Джонатан Горард в одной из своих статей, прямо не связанной с проектом Вольфрама, использует гидродинамику и гиперграфы для описания аккреции материи сверхмассивной чёрной дырой. В общем случае максимальная скорость квантового запутывания (распространения геодезических в многоканальном эволюционном графе) намного выше скорости света (скорости распространения геодезических в релятивистском причинном графе), однако это перестаёт быть так при наличии достаточно высокой плотности массы в пространстве-времени (при наличии достаточно высокой плотности причинных рёбер в многоканальном причинном графе), например, вблизи черной дыры. Горард ставит количество излучаемой квазаром энергии в зависимость от плотности гиперграфов и предсказывает отклонения светимости джетов от предсказаний классической ОТО в 2-3 раза, если пространство-время дискретно на планковском масштабе. Большинство физиков скептически относятся к подобным заявлениям, поскольку никому до сих пор не приходило в голову искать квантово-гравитационные эффекты в наблюдаемом излучении квазаров – оно слишком слабое и медленное на фоне экстремальных условий вблизи сингулярности. Но, как говорится, поживём – увидим, выдержит ли теория проверку временем.

Напоследок приведу цитату из комментария Дэвида Дойча к «Науке нового типа»: «Если идеи, основанные на вычислениях, действительно будут играть фундаментальную роль в физике, это должно произойти через квантовую теорию вычислений». Простоту и вычислимость нельзя определить независимо от законов физики. Насколько легко или трудно смоделировать систему на универсальном компьютере, зависит от физики, лежащей в его основе. Не компьютерные программы определяют протекание физических процессов, а наоборот – физика определяет, какие вентили и вычислительные операции реализовать можно, а какие нельзя. Правила задают лишь последовательное преобразование абстрактных отношений между абстрактными точками – при желании из них можно вывести любую физику любой мыслимой вселенной. Тогда почему мы должны искать именно простые вычислительные правила, а не простые уравнения?

Традиционно каждая следующая физическая теория была сложнее предыдущей, по крайней мере в математическом отношении. Вольфрам доказывает, что может быть и наоборот. Математика его теории довольно простая, если сравнивать её с уравнениями Эйнштейна или лагранжианом КТП. Но какой ценой он избавился от этой сложности в уравнениях? Клеточный автомат вроде Правила 110 может вычислить первые несколько простых чисел и симулировать универсальную машину Тьюринга, но чтобы эта система работала как универсальный компьютер, программа должна быть закодирована на входной ленте чрезвычайно сложным способом. Как пишет Скотт Ааронсон, «…ограничиваясь чрезвычайно короткими программами, мы просто обмениваем невозможный поиск среди программ на невозможный поиск среди входных схем кодирования». Вычисление, которое нужно выполнить для кодирования ввода и декодирования вывода, будет намного сложнее, чем исходная задача, так же как сложность компилятора может намного превышать сложность программ, которые он кодирует. Аналогично и при переводе физических теорий на машинный язык Вольфрама мы упрощаем математику, но усложняем графику и «словесный багаж» — достаточно взглянуть на обилие картинок в статьях и многословные попытки Вольфрама объяснить, о чём же они говорят.

Вывод

Стивену Вольфраму нужно отдать должное – он выжал максимум из вычислительной идеи «всё из бита» (цифровой физики), охватив своей теорией всё, что в принципе можно вычислить и оцифровать. Но на этом пути он столкнулся с вычислительной неприводимостью. Внезапно оказалось, что мы просто не в состоянии найти ту самую короткую программу, которая вычисляет именно нашу вселенную. А ведь это и так было понятно – теорема Хайтина о невычислимости колмогоровской сложности, теорема Тьюринга о неразрешимости проблемы остановки и теорема Гёделя о неполноте в принципе говорили об одном и том же каждая на своём языке. То есть Вольфрам просто расписался в своей неспособности описать Вселенную как детерминированный клеточный автомат. Он построил очередную «теорию чего угодно», предлагающую 100500 рекурсивных функций и не указывающую, какая же из них имеет отношение к нашему миру. В этом плане он не продвинулся дальше струнных теоретиков, которые нашли 10⁵⁰⁰ вселенных с разными константами и не указали, какая же из них. Так может, пора уже смириться с неопределённостью нашей самолокации в мультивселенной и признать все неотличимые для нас миры в равной мере существующими?

Теория Вольфрама в очередной раз подтверждает следствие теоремы Белла и связанных с ней запретов – невозможность воспроизведения квантовой механики локальной теорией со скрытыми параметрами. Классический детерминизм опровергнут тестами Белла раз и навсегда, попытки его воскрешения заведомо обречены на неудачу. Поэтому я бы не придавал особого значения теории Вольфрама, пока не будет доказано, что смоделировать квантовое вычисление на клеточном автомате легче, чем смоделировать клеточный автомат на квантовом компьютере. Квантовые версии клеточных автоматов уже существуют и успешно работают, если что. А вот о клеточно-автоматных версиях квантовых вычислений мы вряд ли когда-нибудь услышим. Как доказал Гордон Мур, даже классический аналоговый компьютер, работающий с действительными числами в непрерывном времени, сможет вычислять больше функций, чем цифровая машина Тьюринга. Что касается потенциала вольфрамовских гиперграфов в объединении КТП и ОТО в единую теорию квантовой гравитации, то моё мнение таково: лучше иметь две несовместимые между собой, но трудноварьируемые и работающие на практике теории, чем одну самосогласованную «теорию чего угодно».