Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
Введение
Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.
Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.
Угловая скорость твердого тела — это первая производная от угла поворота тела по времени
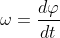
А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении
обычно дается следующее определение
Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки
Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».
При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.
Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.
Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.
Думаю для затравки вполне достаточно, а поэтому — начнем!
1. Свободное движение твердого тела. Тензор поворота
Итак, как известно из традиционного вузовского курса теормеха
Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным
Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом O1 и сферического вокруг полюса.
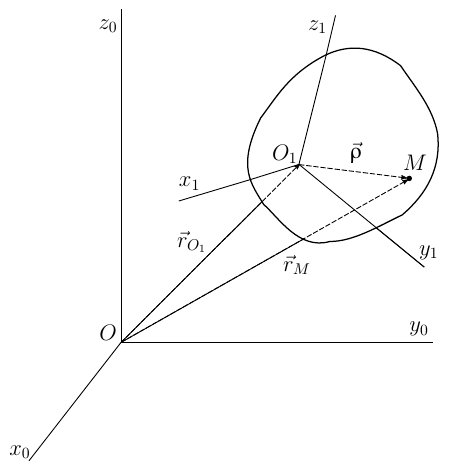
Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.
Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.
Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна (Ox0y0z0) считается неподвижной и называется базовой, другая (Ox1y1z1) жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.
Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.
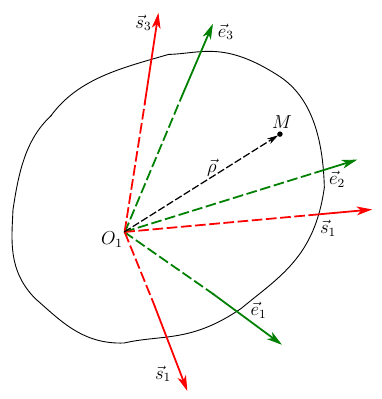
Рис. 2. Ориентация твердого тела в локальном базисе.
Пусть положение полюса O1 задается вектором
Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.
В точке O1 задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер
. Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства
Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера
и по векторам базового репера
Каждый вектор связанного репера можно разложить через векторы базового репера
Подставляем (4) в (2) и сравниваем с (3)
Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора
или в безиндексной форме
где столбцы матрицы
— контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор
действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат
Правая часть (8) — это локальный метрический тензор
В левой части (8) вычисляем скалярное произведение, используя (4)
или
Оператор является по сути обыкновенной матрицей поворота координатной системы. И (10) утверждает, что если транспонированную матрицу поворота умножить на метрический тензор, а результат умножить на матрицу поворота мы получим снова метрический тензор. Можно сделать вывод, что
Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.
В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла
Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.
Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.
Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на
и справа на
откуда незамедлительно получаем
Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.
Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений
При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.
2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену
Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами
Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении
где — скорость полюса;
— скорость точки вокруг полюса.
Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать
Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)
Перейдем в (16) к связанной системе координат, домножив (15) слева на
где — компонента оператора обратного преобразования
.
Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева
Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости
при этом замечая, что
антисимметричный тензор второго ранга, о котором мы говорили в прошлой статье. Таким образом, нам бы доказать, что
является антисимметричным тензором второго ранга. Для этого придется доказать, что (19) меняет знак при перестановка индексов (транспонировании). При этом будем учитывать, что метрический тензор — абсолютно симметричный тензор второго ранга и при транспонировании он не меняется. Поэтому исследуем взаимосвязи между матрицами поворота, для чего нам потребуются выражения (10) и (11). Но прежде чем приступить, докажем ещё одно вспомогательное утверждение
3. Лемма о ковариантной производной метрического тензора
Ковариантная производная метрического тензора равна нулю
Обратимся к понятию ковариантной производной вектора, о которой упоминалось в третьей статье. Тогда мы вывели выражения для контравариантных компонент ковариантной производной от вектора
Как как и любой вектор, компоненты данного вектора можно трансформировать в ковариантные умножением и сверткой с метрическим тензором
А можно продифференцировать ковариантные компоненты непосредственно
Сравнивая (21) и (20) мы приходим к выводу, что равенство возможно лишь в случае если верно утверждение леммы
4. Угловая скорость как антисимметричный тензор второго ранга
Теперь, перепишем (19) в безиндексном виде, учтя уравнение (11)
Далее, нам нужна связь между оператором поворота и его производной — дифференцируем (10) по времени
или, собирая производные от метрического тензора в правой части
Но, производные от метрического тензора в (24) будут равны нулю, в силу равенства нулю ковариантной производной метрического тензора. Значит правая часть (24) равна нулю
Пользуясь свойствами операции транспонирования, преобразуем (25)
Так как и с учетом (23), получаем
Из (26) непосредственно следует антисимметричность тензора (19)
Ну а коль скоро (19) антисимметричный тензор, то мы смело переписываем (18)
Таким образом мы приходим к выводу, что (19) и (23) есть ни что иное как антисимметричный тензор угловой скорости
5. Псевдовектор угловой скорости
Любому антисимметричному тензору можно поставить в соответствие псевдовектор, который мы уже получали в предыдущей статье. Повторим этот результат для тензора угловой скорости
Возможно читателю знаком распространенный подход замены векторного произведения на умножение кососимметричной матрицы, построенной из первого вектора по определенному правилу, на второй вектор. Так вот это правило получается естественным путем, если в качестве инструмента использовать тензорное исчисление. Действительно, вот эта кососимметричная матрица, которой в матричном изложении механики заменяют угловую скорость
Возможно, внимательный читатель увидит, что в полученной матрице знаки противоположны тем, что мы получали в статье, посвященной антисимметричным тензорам. Да, все верно, ведь в той статье мы сворачивали вектор с тензором Леви-Чивиты по его третьему индексу k, тут мы выполняем свертку по среднему индексу j что дает прямо противоположные знаки.
Матрица (30) частенько встречается в литературе, в частности в трудах Д. Ю. Погорелова, но там она вводится как мнемоническое правило. Формула (29) дает четкую связь между вектором угловой скорости и кососимметричной матрицей. Она же дает возможность перейти от (28) к формуле
Что, внезапно, эквивалентно векторному соотношению
Заключение
В этой статье было много математики. И я вынужден пока ограничится этим материалом — статья вышла длинной и насыщенной формулами. Данная тема будет продолжена и углублена в следующих статьях цикла.
Какой же вывод мы можем сделать сейчас? А вот какой
Угловая скорость твердого тела есть антисимметричный тензор, или, соответствующий ему псевдовектор, порождаемый тензором поворота тела относительно базовой системы координат
Для того чтобы написать эту работу потребовалось перелопатить гору литературы. Основные выкладки выполнены автором самостоятельно. Камнем преткновения были матрицы поворота для случая косоугольных координат. Соотношение (10) было не очевидно, и понять эту связь мне помог ужасный по оформлению, но очень толковый сайт «На что похожа математика». Кстати видно, что все соотношения переходят в известные для ортогональных матриц, если метрический тензор сделать единичным.
Разговор о механике твердого тела будет продолжен, а пока — всё. Спасибо за внимание!
Продолжение следует…
ссылка на оригинал статьи http://habrahabr.ru/post/262129/
если студентов начинают учить теормеху с первого курса — это действительно идиотизм. Что касается содержания самой статьи то есть достаточно учебников в которых угловая скорость введена корректно.
Утверждение: «Ковариантная производная метрического тензора равна нулю «, вообще говоря, неверно. Это верно лишь для согласованных с метрикой связностей.