С целью освоения библиотек для работы с нейронными сетями, решим задачу аппроксимации функции одного аргумента используя алгоритмы нейронных сетей для обучения и предсказания аппроксимации.
Вступление
Пусть задана функция f:[x0,x1]->R
Аппроксимируем заданную функцию f формулой
- P(x) = SUM W[i]*E(x,M[i])
где
- i = 1..n
- M[i] из R
- W[i] из R
- E(x,M) = { 0, при x<M; 1/2, при x=M; 1, при x>M
Очевидно, что при равномерном распределении значений M[i] на отрезке (x0,x1) найдутся такие величины W[i], при которых формула P(x) будет наилучшим образом апроксимировать функцию f(x). При этом, для заданных значений M[i], определённых на отрезке (x0,x1) и упорядоченных по возрастанию, можно описать последовательный алгоритм вычисления величин W[i] для формулы P(x).
А вот и нейросеть
Преобразуем формулу P(x) = SUM W[i]*E(x,M[i]) к модели нейросети с одним входным нейроном, одним выходным нейроном и n нейронами скрытого слоя
- P(x) = SUM W[i]*S(K[i]+B[i]) + C
где
- переменная x — «входной» слой, состоящий из одного нейрона
- {K, B} — параметры «скрытого» слоя, состоящего из n нейронов и функцией активации — сигмоида
- {W, C} — параметры «выходного» слоя, состоящего из одного нейрона, который вычисляет взвешенную сумму своих входов.
- S — сигмоида,
при этом
- начальные параметры «скрытого» слоя K[i]=1
- начальные параметры «скрытого» слоя B[i] равномерно распределены на отрезке (-x1,-x0)
Все параметры нейросети K, B, W и C определим обучением нейросети на образцах (x,y) значений функции f.
Сигмоида
Сигмоида — это гладкая монотонная возрастающая нелинейная функция
- S(x) = 1 / (1 + exp(-x)).
Программа
Используем для описания нашей нейросети пакет Tensorflow
# узел на который будем подавать аргументы функции x = tf.placeholder(tf.float32, [None, 1], name="x") # узел на который будем подавать значения функции y = tf.placeholder(tf.float32, [None, 1], name="y") # скрытый слой nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") # выходной слой model = tf.layers.dense(nn, 1, activation=None, name="output") # функция подсчёта ошибки cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost)
Обучение
init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values })
Полный текст
import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 # диапазон аргумента функции test_data_size = 2000 # количество данных для итерации обучения iterations = 20000 # количество итераций обучения learn_rate = 0.01 # коэффициент переобучения hiddenSize = 10 # размер скрытого слоя # функция генерации тестовых величин def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) # исследуемая функция train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) # узел на который будем подавать аргументы функции x = tf.placeholder(tf.float32, [None, 1], name="x") # узел на который будем подавать значения функции y = tf.placeholder(tf.float32, [None, 1], name="y") # скрытый слой nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") # выходной слой model = tf.layers.dense(nn, 1, activation=None, name="output") # функция подсчёта ошибки cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval())
Вот что получилось
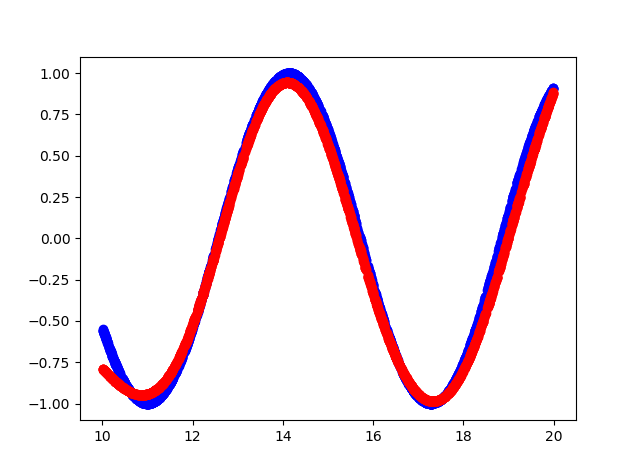
- Синий цвет — исходная функция
- Красный цвет — аппроксимация функции
Вывод консоли
cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019]
Исходный код
ссылка на оригинал статьи https://habr.com/post/428281/