Машинное обучение. Часть 3

Из предыдущих статей цикла мы уже познакомились с основными терминами машинного обучения и классическими задачами. Настало время разобрать методы решения одной из них — задачи классификации. Сегодня мы разберем метод ближайших соседей.

Конечно, мы помним, что задача классификации формулируется следующим образом:

Нам дано некоторое множество объектов X и конечное множество номеров классов Y. Определено отображение ƒ*:X→Y. Причем известно, что некоторым элементам x∈X соответствуют некие классы из множества C. Задача классификации заключается в нахождении функции ƒ, аппроксимирующей ƒ* на всех элементах из X.

Оценка качества классификации

На каждом объекте x из обучающей выборки можно вычислить функцию потерь построенного алгоритма ƒ. Обозначим функцию потерь за L, тогда, L_f(x)=[f*(x)≠f(x)]. Средняя сумма ошибок R (эмпирический риск) на всей обучающей выборке скажет нам о качестве построенного алгоритма. R(ƒ)= (1/N)∑L_ƒ(x_i), для i от 0 до N. Очевидно, что R нужно минимизировать.

Принцип минимизации эмпирического риска.

Функционал эмпирического риска R должен минимизироваться. Это даст нам более высокое качество классификации входных данных. Добиться этого не сложно, достаточно использовать один из общеизвестных методов:

1. Метод наименьших квадратов R(ƒ)=(1/N)∑(y_i-ƒ(x_i))²
2. Метод максимального правдоподобия R(p)=-(1/N)∑ln(p(x_i))

Однако, полностью минимизировав R мы получим переобученый алгоритм, который слишком приспособлен к обучающим данным. Но хороший алгоритм классификации должен правильно работать не только на обучающей выборке, но и за ее пределами. Мы введем термин обобщающей способности — способности алгоритма допускать мало ошибок на обучающих данных после обучения. На практике оценить обобщающую способность можно при помощи скользящего контроля по обучающей выборке.

Скользящий контроль

Скользящий контроль позволяет оценить насколько хорошо алгоритм обобщает данные. При этом фиксируется некоторое множество разбиений исходной выборки на обучающую и контрольную. Для каждого из разбиений выполняется настройка алгоритма по обучающей подвыборке и оценивается его средняя ошибка на контрольной. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках. Минимум функции ошибки на скользящем контроле важен для настройки параметров алгоритмов и оценки их качества.

Метод ближайших соседей

Предварительные сведения

Далее, я буду предполагать, что читатель знаком с университетским курсом теории вероятностей. В случае, если у читателя возникнут вопросы или недопонимания, я готов ответить на них в комментариях.

Сначала введем два определения

1. Метод максимального правдоподобия заключается в максимизации условной вероятности данных при гипотезе. Т.е h=argmax(P(D|h*)).
2. Метод максимальной апостериорной вероятности заключается в максимизации условной вероятности гипотезы при данных. Т.е h=argmax(P(h*|D)).

В случае задачи классификации гипотезой является принадлежность объекта к некоторому классу. Учитывая принцип минимизации эмпирического риска и метод максимальной апостериорной вероятности, мы можем сказать, что оптимальным классификатором является ƒ(x)=argmax(P(y|x)) для y∈Y. Однако, очевидно, что функцию P(x|y) найти из обучающей выборки невозможно. Нам придется находить ее каким-либо другим образом.

Идея алгоритма классификации с помощью метода ближайших соседей состоит в аппроксимации апостериорной вероятности класса P(y|x) через объекты обучающей выборки и расстояния до них. Алгоритм относится к классу алгоритмов ленивого обучения, т.е он обучается, запоминая обучающую выборку. Для работы алгоритма необходима метрика, то есть, пространство объектов должно быть метрическим.

Метод k ближайших соседей

Объекту x присваивается класс, характерный для большинства из k ближайших по метрике объектов ƒ(x)=argmax(∑(ƒ*(c_i = y))). Сумма по i от 1 до k, {c₁,c₂,…,c_k} — ближайшие к x объекты, k — параметр, существенно влияющий на качество классификации.

Метод k взвешенных ближайших соседей

В некоторых случаях максимум может быть выражен неявно. В этом случае к нам приходит на помощь следующая модификация формулы: ƒ(x)=argmax(∑(ƒ*(c_i = y)w(i))). Сумма по i от 1 до k, {c₁,c₂,…,c_k} — ближайшие к x объекты, k — параметр, существенно влияющий на качество классификации, w(i) — весовая функция от ранга объекта. Этот алгоритм является более точным и гибким, т.к настройке подлежат k и w(i).

Метод парзеновских окон

Весовую функцию можно ввести не от ранга, а от расстояния до объекта. В этом случае не нужно выбирать ближайшие объекты — дальние объекты сами по себе будут иметь маленький вес.

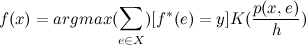
Параметр h называется шириной парзеновского окна. Функция K является произвольной положительной невозрастающей функцией.

Алгоритм

Входные данные: x — объект, подлежащий классификации, множество пар {t_i,ƒ(t_i)}_i=T — обучающая выборка, параметр k, метрика p.

Выходные данные: класс, определенный для объекта x.

Шаги алгоритма:

1. Найти метрики p(x,t) для t∈T
2. Отсортировать обучающую выборку T по убыванию метрики p(x,t), t∈T.
3. Выбрать первые k объектов отсортированной выборки.
4. Просуммировать весовую функцию по всем объектам в соответствующие классу объекты ассоциативного массива. (В случае метода k ближайших соседей, это 1, в случае метода k взвешенных ближайших соседей это w(i), а в случае парзеновских окон это K(p/h))
5. Выбрать из полученного ассоциативного массива ключ, которому соответствует максимальное значение — класс объекта x.

Примеры работы алгоритма

Классификация абстрактных объектов

Рассмотрим работу алгоритма на примере классификации некоторых абстрактных объектов.

На изображении цветными точками представлены объекты из обучающей выборки. Серые точки алгоритму предстоит классифицировать по 4 классам, выделенным разными цветами.

Результат работы алгоритма:

Классификация изображений

Рассмотрим задачу, которую решали исследователи Center For Biological and Computation Learning, MIT. На вход классификатору подается обучающая выборка из двух наборов по 350 изображений размером 19×19 пикселей. В первом наборе лица людей, во втором — все что угодно, но не лица. Классификатору предстоит научиться отличать изображения с лицами от изображений без них.

Несколько изображений из обучающей выборки:

В качестве тестовых данных программе подается 50 изображений для классификации. Изображения представляют собой примерно следующий ряд:

При использовании метода k ближайших соседей качество работы алгорима можно представить графиком:

А при использовании метода парзеновских окон качество несколько иное:

Повышение качества

Существует несколько методов повышения качества классификации:

1. Выбор более подходящей метрики
2. Фильтрация шумов
3. Понижение размерности данных
4. Выбор эталонных объектов

Вычислительная сложность алгоритма складывается из сортировки всей обучающей выборки O(nln(n)) и обработки k ближайших объектов O(k). Однако, как правило, большую часть времени работы алгоритма занимает нахождение расстояния между объектами.

В качестве вывода

Таким образом, мы разобрали принцип минимизации эмперического риска, аппроксимацию апостеорной вероятности ближайшими соседями, узнали что представляют из себя методы ближайших k соседей, ближайших k взвешенных соседей, метод парзеновских окон. Рассмотрели примеры классификации абстрактных объектов и изображений. В следующий раз мы разберем еще один метод классификации.

Для удобства, в конце каждой статьи находится список ссылок на остальные.

1. История и введение.
2. Пере/недо-обучение и классические задачи.
3. Метод ближайших соседей в задачах классификации.

В целях улучшения цикла статей прошу принять участие в опросе.