Wolfram-Math-in-Logistics: Маятниковые маршруты

Как и обещал в своём прошлом посте (тут), что в случае если он будет «принят», я продолжаю цикл статей об использовании Wolfram Mathematica для решения небольших прикладных задач в логистике. Жаль только читатели поскупились на комментарии.
Сегодня мы рассмотрим маятниковые маршруты. Мы будем преследовать две цели: с одной стороны рассмотрим три вида маятниковых маршрутов, а именно маятниковый маршрут с холостым обратным пробегом, с не полностью груженым обратным пробегом, с полностью груженым обратным пробегом, и их технико-эксплуатационные показатели, с другой рассмотрим как можно автоматизировать расчёт этих показателей, дабы избавить себя от излишнего вбивания чисел в калькулятор. Трудно сказать насколько такая автоматизация эффективна и полезна, но работать над этим было по крайней мере интересно.
Под катом много картинок, но не бойтесь, их общий вес около 640 КБ. Как говорил один советский летчик-космонавт «Поехали!».

Думаю все понимают что такое маршруты и почему они называются маятниковыми. Всем будут понятны показатели этих маршрутов: длина маршрута, груженный пробег, холостой пробег и тп. Единственное, что может вызвать непонимание это определения оборота и ездки, где:

• оборот автомобиля — законченный цикл движения, т.е. движение от начального до конечного пункта и обратно;
• ездка — цикл транспортного процесса, т.е. движение от начального до конечного пункта.

Маятниковый маршрут с обратным холостым пробегом

Первым делом необходимо взглянуть на схематическое изображение подобного маршрута, чтобы иметь представление о том, с чем имеем дело. Для этого построим граф. Граф, он же Graph в Mathematica, идеально подходит для такого рода задачи, когда нужно отобразить несколько грузопунктов и соединить их линиями, длина которых нам сейчас не важна.

Хорошо, но совершенно не ясно где какой грузопункт и не ясно что значат эти стрелки. При помощи EdgeLabels и VertexLabels, названия которых говорят сами за себя, добавим текст в наш граф.

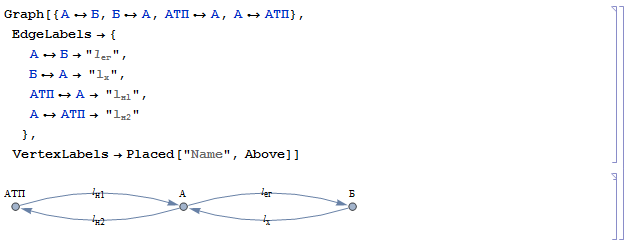
Уже лучше, но внешне выглядит не похоже на маятниковый маршрут, пора изменить это. Параметр GraphLayout с значением CircularEmbedding позволяет нам «закрутить» граф.

ImagePadding необходим для того, что бы весь текст помещался в рамки отображения графа. Отлично, остаётся только добавить красок и навести марафет.

Теперь, когда у нас перед глазами образец, рассчитаем показатели данного вида маршрута.

Дано

Решение

1. Определяем время оборота автомобиля на маршруте, ч:

2. Определяем количество оборотов за время работы автомобиля на маршруте:

3. Определяем возможную массу груза, перевозимую автомобилем за день, т:

4. Определяем необходимое количество автомобилей для перевозки 320т. груза:

5. Определяем коэффициент использования пробега:

Маятниковый маршрут с не полностью груженым обратным пробегом

Попробуем нарисовать граф. Почему попробуем? Потому что мне так и не удалось довести его до такого состояния, когда автоматически выводится граф в готовом виде. И только при помощи рук возможно отобразить его в необходимом виде. Что имеем:

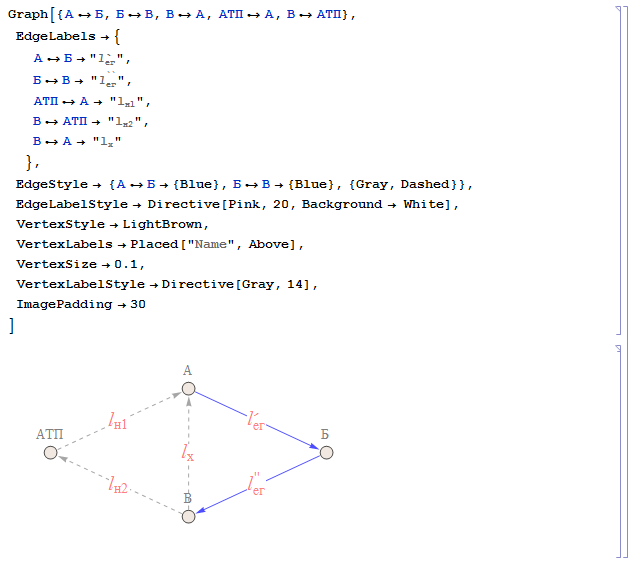
Надеюсь что более продвинутые в Wolfram Mathematica пользователи помогут мне получить необходимый результат.

Дано

Решение

1. Определяем время оборота автомобиля, ч:

2. Определяем количество оборотов:

3. Определяем количество ездок:

4. Определяем производительность автомобиля, т:

5. Определяем необходимое количество автомобилей:

6. Определяем коэффициент использования пробега за 1 оборот:

Маятниковый маршрут с полностью груженым обратным пробегом

С построением этого графа проблем не возникло:

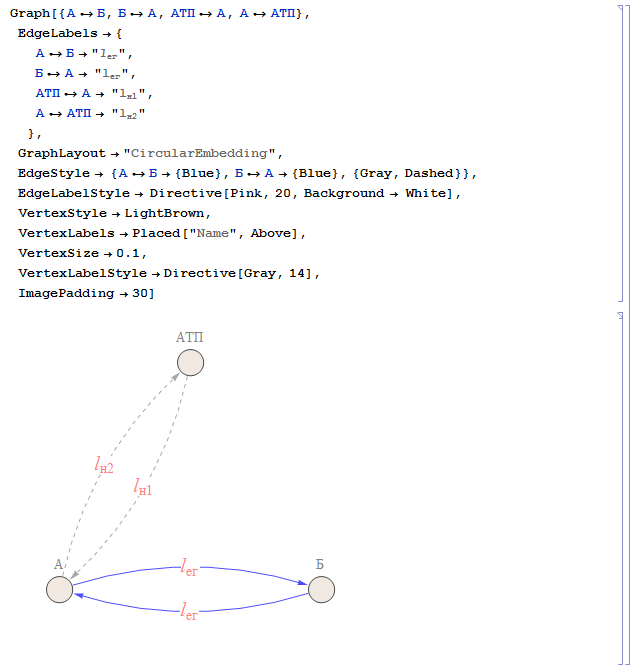
Дано

Решение

1. Определяем время оборота автомобиля, ч:

2. Определяем количество оборотов и ездок:

3. Объём перевозки груза, т:

4. Необходимое количество автомобилей для перевозки грузов:

5. Определяем коэффициент использования пробега за один день:

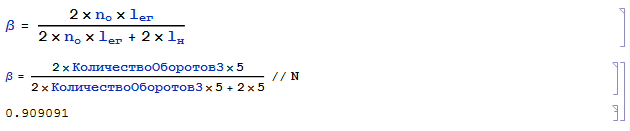
Автоматизация расчёта показателей маятниковых маршрутов

Проделано не мало работы, но какой в ней смысл, если большая часть формул считается на калькуляторе за полминуты? Поэтому мы не остановимся на достигнутом и пойдём дальше. Мы создадим интерфейс, который будет за нас считать все показатели, наше дело только «скормить» ему исходные данные.
Начнём с простого, а именно с поля ввода (оно же и поле вывода результата):

Отлично, но непонятно что следует вводить или что выводится в этом поле. При помощи Row создаём строку, состоящую уже из нескольких элементов:

Поле вывода будет соответственно содержать в себе некую расчётную формулу, например:

Скомпонуем несколько таких полей для ввода и вывода:

Я думаю в структуре компоновки легко разобраться. Множество Row выстраиваются в колонки Column. Сами строки чередуются с описанием для них, простые строки. Style позволяет присвоить тексту какой-нибудь цвет, вроде Brown, Gray и тп. Результат выглядит так:

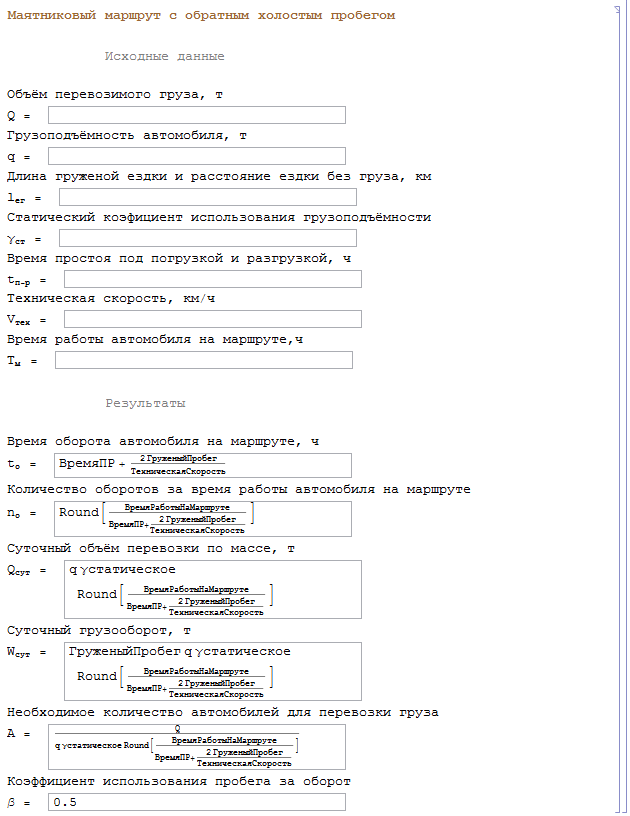
Упакуем всю структуру сначала в Panel, чтобы получить рамку, а затем ещё и в Style, чтобы получить возможность изменять оформление полей, а точнее их размер:

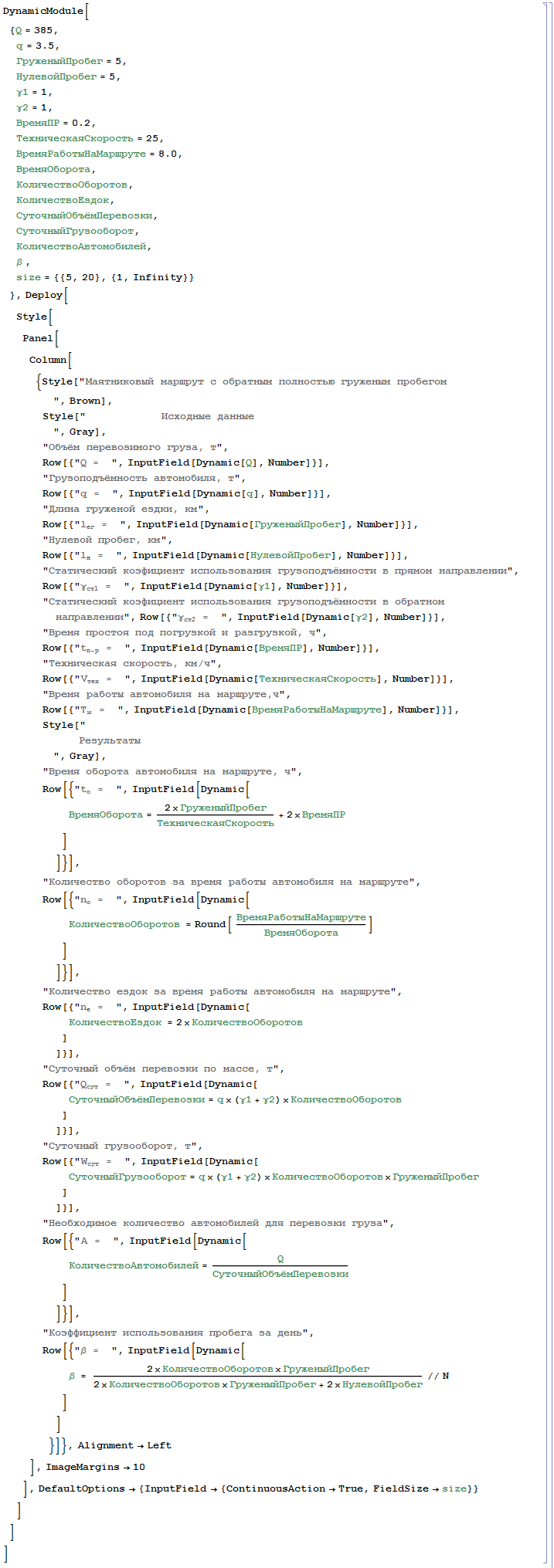
Но и это не всё. Всю полученную структуру помещаем в DynamicModule[{Локальные переменные}, Deploy[]]. Очевидно, что это позволит нам создать набор локальных переменных, полностью изолировать структуру от любых расчётов вне её. Такая структура будет легко переносима или легко импортируется из одного блокнота в другой. Результат:

Окончательный внешний вид

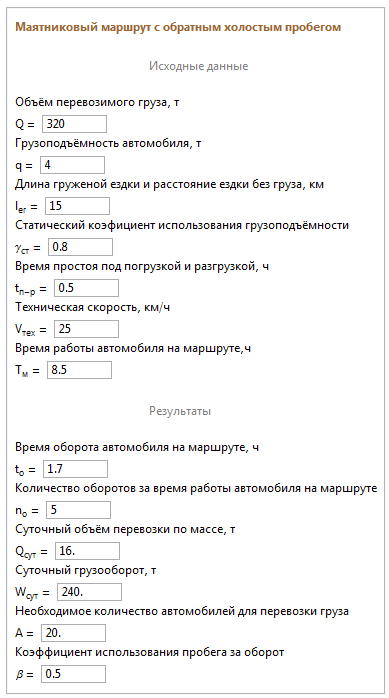
Автопоказатели для маятникового маршрута с обратным холостым пробегом

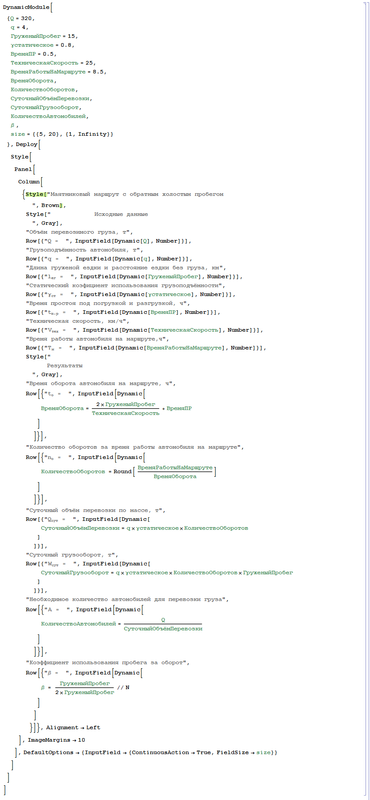
Автопоказатели для маятникового маршрута с не полностью груженым обратным пробегом

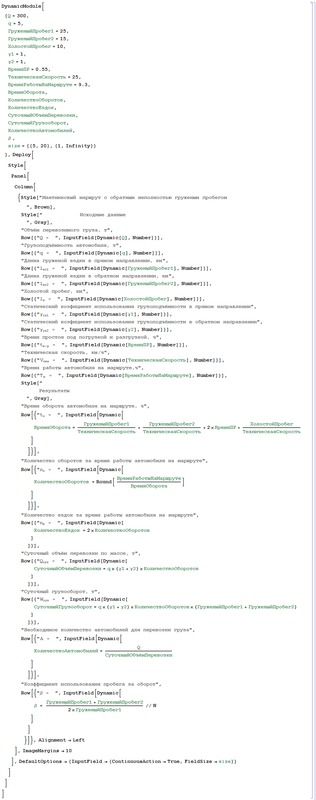
Автопоказатели для маятникового маршрута с полностью груженым обратным пробегом

Используемая литература

Неруш Ю. М. Логистика: учеб. — 4-е изд., перераб. и доп. — М.: ТК Велби, H54 Изд-во Проспект, 2008 — 520 с.
ISBN 978-5-482-01995-5
Рекомендую купить, например, здесь: OZON.ru

Исходники

Проект в виде репы на GitHub — Wolfram-Math-in-Logistics
Буду очень рад видеть ваши вопросы, рекомендации и возможно форки.

Подборка ссылок

• Wolfram-Math-in-Logistics: Прогнозирование материалопотока и товарооборота;
• Wolfram-Math-in-Logistics: Маятниковые маршруты;
• Ждите ещё.