Сказка о потерянном времени

Если честно, то не совсем и сказка, а суровая жизнь. Но время ведь потеряно совершенно настоящее, хоть и с пользой. А началось всё совершенно случайно. На одном сайте один умный товарищ написал пост о гипотезе Эйлера. Суть достаточно проста. Гипотеза Эйлера утверждает, что для любого натурального числа n>2 никакую n-ю степень натурального числа нельзя представить в виде суммы (n-1) n-х степеней других натуральных чисел. То есть, уравнения:

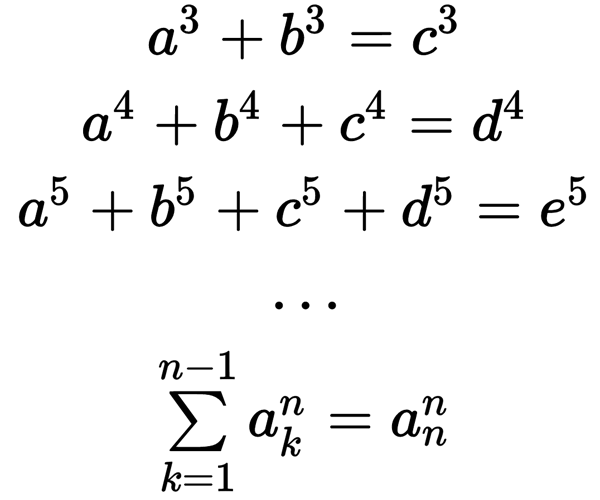
не имеют решения в натуральных числах.

Ну собственно так оно и было до 1966 года…

Пока Л. Ландер (L. J. Lander), Т. Паркин (T. R. Parkin) и Дж. Селфридж ( J. L. Selfridge) не нашли первый контрпример для n = 5. И сделали они это на суперкомпьютере того времени — CDC 6600, разработанного под командованием не безызвестного Сеймура Крэя (Seymour Roger Cray) и имел этот суперкомпьютер производительность аж 3 MFLOPS. Их научная работа выглядела так:

То есть простым перебором на суперкомпьютере они нашли числа степени 5, которые опровергали гипотезу Эйлера: 27⁵ + 84⁵ + 110⁵ + 133⁵ = 144⁵.
И всё бы ничего, но другой умный товарищ спросил: "интересно, а вот кто–нибудь из программистов может набросать код для супер–современного i5 по поиску еще таких совпадений?…".
Как вам уже понятно, предложение сработало как красная тряпка. Первое решение оказалось достаточно красивым и написанным с умом. Суть в том, что вначале считаем пятые степени для 1-N чисел, заносим их в таблицу и рекурсивно начинаем перебирать с самого низу четыре слагаемых пятых степеней, попутно ища в таблице сумму получившихся значений. Если нашли — вот оно и решение (индекс в таблице будет числом, степень которого мы нашли).

Вот этот первый вариант пользователя 2Alias:

	#include <iostream> 	#include <algorithm> 	#include <stdlib.h> 	#include <vector> 	#include <unordered_map> 	  	using namespace std; 	typedef long long LL; 	const int N = 250; 	  	LL p5(int x) 	{ 	    int t = x * x; 	    return t * (LL) (t * x); 	} 	  	vector<LL> p; 	std::unordered_map<LL, int> all; 	int res[5]; 	  	void rec(int pr, LL sum, int n) 	{ 	    if (n == 4) 	    { 	        if (all.find(sum) != all.end()) 	        { 	            cout << "Ok\n"; 	            res[4] = all[sum]; 	            for (int i = 0; i < 5; ++i)                 cout << res[i] << " "; 	            cout << "\n"; 	            exit(0); 	        } 	        return; 	    } 	    for (int i = pr + 1; i < N; ++i) 	    { 	        res[n] = i; 	        rec(i, sum + p[i], n + 1); 	    } 	} 	  	int main() 	{ 	    for (int i = 0; i < N; ++i) 	    { 	        p.push_back(p5(i)); 	        all[p.back()] = i; 	    } 	    rec(1, 0, 0); 	    return 0; 	} 

И как оно обычно бывает, я подумал, а можно ли быстрее? Заодно у людей возник вопрос, а что будет если проверить в этом деле C#. Я в лоб переписал решение на C# и программа показала примерно такой же результат по времени. Уже интересно! Но оптимизировать всё же будем C++. Ведь потом всё легко перенести в C#.
Первое что пришло в голову — убрать рекурсию. Хорошо, просто введём 4 переменные и будем их перебирать с инкрементом старших при переполнении младших.

	// N - до какого числа ищем 1 - N в степени 5 	// powers - массив с посчитанными заранее степенями 	// all = unordered_map< key=степень числа, value=само число>  	uint32 ind0 = 0x02; // ищем начиная с 2 	uint32 ind1 = 0x02; 	uint32 ind2 = 0x02; 	uint32 ind3 = 0x02; 	uint64 sum = 0;  	while (true) 	{ 		sum = powers[ind0] + powers[ind1] + powers[ind2] + powers[ind3]; 		if (all.find(sum) != all.end()) 		{ 			// нашли совпадение - ура!! 			foundVal = all[sum]; 			... 		}  		// следующий 		++ind0; 		if (ind0 < N) 		{ 			continue; 		} 		else 		{ 			ind0 = 0x02; 			++ind1; 		} 		if (ind1 >= N) 		{ 			ind1 = 0x02; 			++ind2; 		} 		if (ind2 >= N) 		{ 			ind2 = 0x02; 			++ind3; 		} 		if (ind3 >= N) 		{ 			break; 		} 	} 

И тут же результат стал хуже. Ведь нам будут встречаться множество одинаковых сумм, большую часть которых рекурсивный алгоритм обходит. Допустим у нас числа от 1 до 3, переберём их:

111
112
113
121 < — уже было!
122
123
131 < — уже было!
132 < — уже было!
133
…

Значит придётся смотреть комбинаторику, но мне это не сильно помогло, так как достаточного объёма знаний по этой теме я не имею, пришлось выписывать примерно такой же пример на бумажку и подумать. И решение нашлось: при инкременте старших разрядов, не надо сбрасывать младшие на самый минимум, а присваивать значение старшего всем младшим — так мы отсечём лишнее.

Код увеличения индексов стал таким:

	... 	// следующий 	++ind0; 	if (ind0 < N) 	{ 		continue; 	} 	else 	{ 		ind0 = ++ind1; 	} 	if (ind1 >= N) 	{ 		ind0 = ind1 = ++ind2; 	} 	if (ind2 >= N) 	{ 		ind0 = ind1 = ind2 = ++ind3; 	} 	if (ind3 >= N) 	{ 		break; 	} 

Ура! И уже сразу чуть быстрее. Но что нам говорит профайлер? Большую часть времени мы сидим в unordered_map.find…
Начинаю вспоминать алгоритмы поиска и разнообразные знания(вплоть до демосцены). А что если перед проверкой в unordered_map как-то быстро отсекать часть ненужного?
Так появился ещё один массив, уже битовый (bitset). Так как числа нам в него не занести (они слишком большие), придётся быстро делать хэш из степени, приводить его к количеству бит в массиве и отмечать там. Всё это надо делать при построении таблицы степеней. В процессе написания оказалось, что std::bitset немного медленнее простого массива и минимальной логики что я набросал. Ну да ладно, это ерунда. А в целом ускорение оказалось существенным, около двух раз.
Много экспериментируя с размером bitset’a и сложностью хэша стало понятно, что по большому счёту влияет только память, причём для разных N по-разному и большая степень фильтрации обращений к unordered_map.find лучше только до определённого предела.

Выглядеть это стало примерно так:

	... 	// тут теперь мы быстро фильтруем сумму по хэшу и битовой таблице 	if (findBit(sum)) 	{ 		// и только потом проверяем в map, а проверять надо - ведь у нас коллизии из-за хэша 		if (all.find(sum) != all.end()) 		{ 			// нашли! 		} 	} 	// следующий 	... 

Дальше возникла проблема номер два. Первый пример из далёкого 1966 года имел максимальное число 144⁵ (61 917 364 224), а второй (2004 год) уже 85359⁵ (4 531 548 087 264 753 520 490 799) — числа перестают влезать в 64 бита…
Идём самым простым путём: берём boost::multiprecision::uint128 — вот его нам хватит надолго! Это из-за того, что я пользуюсь MS CL, а он просто не поддерживает uint128, как все остальные компиляторы. Кстати, за время поиска решения проблемы uint128 и компиляторов я ещё узнал про шикарный сайт — Compiler Explorer. Прямо в онлайне можно скомпилировать код всеми популярными компиляторами разных версий и посмотреть во что они транслируют его(ассемблер), причём с разными флагами компиляции. MS CL тоже есть, но на бета сайте. И помимо С++ есть Rust, D и Go. Собственно, по коду и стало понятно, что MS CL совсем не понимает 128 составные целые, все компиляторы транслируют перемножение двух 64 битных в 128 битную структуру за три умножения, а MS CL — за четыре. Но вернёмся к коду.
С boost::multiprecision::uint128 производительность упала в 25 раз. И это как-то совсем неправильно, ведь в теории должно быть не более 3х раз. Забавно, что на столько же упала производительность C# версии с типом decimal (он хоть и не совсем целочисленный, но его мантисса 96бит). А предварительная фильтрация обращений к Directory (своеобразный аналог unordered_map из STL) — работает хорошо, ускорение очень заметно.

Ну значит сами понимаете — стало обидно. Столько уже сделано и всё зря. Значит будем изобретать велосипед! То есть простой тип данных uint128. По сути, нам же нужно только присваивание, сравнение, умножение и сложение. Не так и сложно, но процесс в начале пошёл не туда, так как сначала я взялся за умножение и дошло это до использования ассемблера. Тут не чем гордиться, лучше всего себя показали интринсики. Почему процесс пошёл не туда? А нам умножение-то и не важно. Ведь умножение участвует только на этапе просчёта таблицы степеней и в основном цикле не участвует. На всякий случай в исходниках остался файл с умножением на ассемблере — вдруг пригодится.

	friend uint128 operator*(const uint128& s, const uint128& d) 	{ 		// intristic use 		uint64 h = 0; 		uint64 l = 0; 		uint64 h2 = 0; 		l = _mulx_u64(d.l, s.l, &h); 		h += _mulx_u64(d.l, s.h, &h2); 		h += _mulx_u64(d.h, s.l, &h2); 		return uint128( h, l); 	} 

Со своим uint128 производительность тоже, конечно, просела, но всего на 30% и это отлично! Радости полно, но профайлер не забываем. А что если совсем убрать unordered_map и сделать из самописного bitset’a подобие map’a? То есть после вычисления хэша суммы мы можем уже использовать это число как индекс в ещё одной таблице(unordered_map тогда не нужен совсем).

	// вот так выглядит самописный map 	boost::container::vector<CompValue*> setMap[ SEARCHBITSETSIZE * 8 ]; 	...  	// ComValue просто контейнер для степени и числа 	struct CompValue 	{ 	... 		mainType fivePower; 		uint32 number; 	};  	// Поиск по битовому массиву и самописному map 	inline uint32 findBit(mainType fivePower) 	{ 		uint32 bitval = (((uint32)((fivePower >> 32) ^ fivePower))); 		bitval = (((bitval >> 16) ^ bitval) & SEARCHBITSETSIZEMASK); 		uint32 b = 1 << (bitval & 0x1F); 		uint32 index = bitval >> 5; 		if((bitseta[index] & b) > 0) 		{ 			for (auto itm : setMap[bitval]) 			{ 				if (itm->fivePower == fivePower) 				{ 					return itm->number; 				} 			} 		} 		return 0; 	} 

Так как проект совершенно несерьёзный и никакой полезной нагрузки не нёс, я сохранял все способы перебора, поиска и разных значений через жуткий набор дефайнов и mainType как раз один из них — это тип куда пишется степень числа, чтобы подменять его при смене только один раз в коде. Уже на этом этапе все тесты можно проводить с uint64, uint128 и boost::multiprecision::uint128 в зависимости от дефайнов — получается очень интересно.

И знаете, введение своего map’а — помогло! Но не на долго. Ведь понятно, что map не просто так придуман и используется везде, где только можно. Опыты — это, конечно, подтверждают. При определённом N (ближе к 1 000 000), когда все алгоритмы уже тормозят, голый map(без предварительного bitset’a) уже обходит самописный аналог и спасает только значительное увеличение битового массива и массива где хранятся наши значения степеней и чисел, а это огромное количество памяти. Примерный мультипликатор около N * 192, то есть для N = 1 000 000 нам нужно больше 200мб. А дальше ещё больше. К этому моменту ещё не пришло понимание, почему так падает скорость с ростом массива степеней, и я продолжил искать узкие места вместе с профайлером.
Пока происходило обдумывание, я сделал все испробованные способы переключаемыми. Ибо мало ли что.
Одна из последних оптимизаций оказалось простой, но действенной. Скорость C++ версии уже перевалила за 400 000 000 переборов в секунду для 64бит ( при N = 500 ), 300 000 000 переборов для 128 бит и всего 24 000 000 для 128 бит из boost, и влиять на скорость уже могло практически всё. Если перевести в Гб, то чтение получается около 20Гб в секунду. Ну может я где-то ошибся…

Вдруг стало понятно, что пересчитывать всю сумму на каждом проходе не надо и можно ввести промежуточную. Вместо трёх сложений будет одно. А пересчитывать промежуточную только при увеличении старших разрядов. Для больших типов это, конечно, сильнее заметно.

	mainType sum = 0U, baseSum = 0U;  	baseSum = powers[ind1] + powers[ind2] + powers[ind3];  	while(true) 	{ 		sum = baseSum + powers[ind0]; 		...  		// refresh without ind0 		baseSum = powers[ind1] + powers[ind2] + powers[ind3]; 	} 

Тут уже задача начинала надоедать, так как быстрее уже не получалось и я занялся C# версией. Всё перенёс туда. Нашёл уже готовый, написанный другим человеком UInt128 — примерно такой же простой, как и мой для C++. Ну и, конечно, скорость сильно подскочила. Разница оказалась меньше чем в два раза по сравнению с 64 битами. И это у меня ещё VS2013, то есть не roslyn (может он быстрее?).
А вот самописный map проигрывает по всем статьям Directory. Видимо проверки границ массивов дают о себе знать, ибо увеличение памяти ничего не даёт.
Дальше уже пошла совсем ерунда, даже была попытка оптимизировать сложение интринсиками, но чисто C++ версия оказалась самой быстрой. У меня почему-то не получилось заставить инлайниться ассемблерный код.

И всё же постоянно не отпускало чувство, что я что-то не вижу. Почему при росте массива всё начинает тормозить? При N = 1 000 000 производительность падает в 30 раз. Приходит в голову кэш процессора. Даже попробовал интринсик prefetch, результата — ноль. Пришла мысль кэшировать часть перебираемого массива, но при 1 000 000 значений (по 20 байт) как-то глупо выглядит. И тут начинает вырисовываться полная картина.
Так как числа у нас 4, есть 4 индекса, которые берут значения из таблицы. Таблица у нас постоянно возрастающих значений и сумма всех четырёх степеней у нас постоянно возрастающая (до переключения старших индексов). И разность степеней становится всё больше и больше.
2⁵ это 32, а 3⁵ это уже 243. А что если искать прямо в том же массиве просчитанных степеней обычным линейным поиском, сначала выставляя начальное значение на самый большой индекс и сохраняя индекс последнего найденного меньшего значения чем наша сумма (следующая будет больше) и использовать этот сохранённый индекс как начальную точку при следующем поиске, ведь значения не будут сильно меняться… Бинго!

Что в итоге?

	uint32 lastRangeIndex = 0;  	// линейный поиск в массиве степеней 	inline uint32 findInRange(mainType fivePower, uint32 startIndex) 	{ 		while (startIndex < N) 		{ 			lastRangeIndex = startIndex; 			if (powers[startIndex] > fivePower) 			{ 				return 0; 			} 			if (powers[startIndex] == fivePower) 			{ 				return startIndex; 			} 			++startIndex; 		} 		return 0; 	}  	...  	// главный цикл поиска 	baseSum = powers[ind1] + powers[ind2] + powers[ind3]; 	while (true) 	{ 		sum = baseSum + powers[ind0];  		foundVal = findInRange( sum, lastRangeIndex); 		if (foundVal > 0) 		{ 			// нашли! 		}  		// следующий 		++ind0; 		if (ind0 < N) 		{ 			continue; 		} 		else 		{		 			ind0 = ++ind1; 		} 		if (ind1 >= N) 		{ 			ind0 = ind1 = ++ind2; 		} 		if (ind2 >= N) 		{ 			ind0 = ind1 = ind2 = ++ind3; 		} 		if (ind3 >= N) 		{ 			break; 		} 		// сброс индекса на начальное значение при изменении старших индексов 		lastRangeIndex = 0x02; 		if (ind1 > lastRangeIndex) 		{ 			lastRangeIndex = ind1; 		} 		if (ind2 > lastRangeIndex) 		{ 			lastRangeIndex = ind2; 		} 		if (ind3 > lastRangeIndex) 		{ 			lastRangeIndex = ind3; 		} 		// refresh without ind0 		baseSum = powers[ind1] + powers[ind2] + powers[ind3]; 	} 

Скорость на маленьких значениях N немного уступает самописному map, но как только растёт N — скорость работы даже начинает расти! Ведь промежутки между степенями больших N растут чем дальше, тем больше и линейный поиск работает всё меньше! Сложность получается лучше O(1).

Вот вам и потеря времени. А всё почему? Не надо бросаться грудью на амбразуру, посиди — подумай. Как оказалось, самый быстрый алгоритм — это линейный поиск и никакие map/bitset не нужны. Но, безусловно, это очень интересный опыт.

Хабр любит исходники и они есть у меня. В коммитах можете даже посмотреть историю «борьбы». Там лежат обе версии и C++, и C#, в котором этот трюк, конечно, так же отлично работает. Проекты хоть и вложены один в другой, но, конечно, никак не связаны.
Исходники ужасны, в начале находятся дефайны, где можно задать основное значение (uint64, uint128, boost::uin128/decimal(для C#), библиотеку можно переключать std/boost (boost::unordered_map оказался быстрее std::unordered_map примерно на 10%). Так же выбирается алгоритм поиска (правда сейчас вижу, что предварительный фильтр для unordered_map в версии C++ не пережил правок, но он есть в коммитах и в C# версии) unordered_map, самописный bitset и range(последний вариант).

Вот такая вот сказка и мне урок. А может и ещё кому будет интересно. Ведь много каких значений ещё не нашли…

* к/ф Сказка о потерянном времени, 1964г.
ссылка на оригинал статьи https://habrahabr.ru/post/317588/