Автоэнкодеры и сильный искусственный интеллект

Теория автоэнкодеров и генерирующих моделей последнее время получила серьезное развитие, но достаточно мало работ посвящено тому, как можно использовать их в задачах распознавания. При этом свойство автоэнкодеров получать скрытую параметрическую модель данных и математические следствия из этого дают возможность связать их с Байесовскими методами принятия решения.

В статье предложен оригинальный математический аппарат «набор автоэнкодеров с общим латентным пространством», который позволяет выделять абстрактные понятия из входных данных и демонстрирует способность к «one-shot learning». Кроме того, с его помощью можно преодолеть многие фундаментальные проблемы современных алгоритмов машинного обучения, основанных на многослойных сетях и подходе «Deep learning».

Предпосылки

Искусственные нейронные сети, обучающиеся с помощью механизма обратного распространения ошибок, практически вытеснили иные подходы во многих задачах распознавания и оценки параметров. Но они обладают рядом недостатков, которые, кажется, не устранимы без серьезного пересмотра подхода:

1) крайняя неустойчивость к входным данным, не встречающимся в обучающей выборке (в том числе и в случае Adversarial attacks)

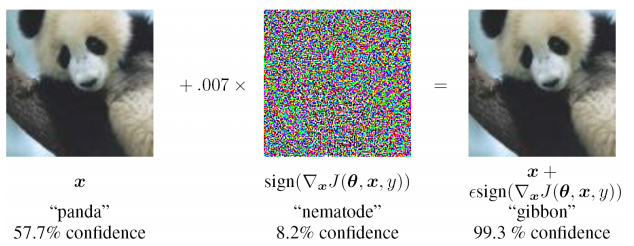
2) сложно оценить источник проблемы и локально дообучить на одном из уровней (приходится просто дополнять обучающую выборку и переобучать), т.е. проблема «черного ящика»

3) не предусматривается возможность различной трактовки одной и той же входной информации, игнорируется статистическая природа наблюдаемых данных

Занимаясь решением прикладных задач, и, оперевшись на ряд существующих работ, я предлагаю подход, который заметно отличается от существующих, устраняет ряд их недостатков и применим для решения прикладных задач в различных областях машинного обучения.

Автоэнкодер для оценки плотности распределения

В теории принятия решения очень важное место занимает плотность распределения (или функция распределения) случайных величин. Необходимо иметь оценки функций распределения для расчета апостериорного риска.

Оказывается, что автоэнкодеры очень естественны для выполнения оценки функций распределения. Объяснить это можно следующим образом: обучающий набор данных определяется плотностью их распределения. Чем выше плотность обучающих примеров вокруг локальной точки во входном пространстве, тем лучше автоэнкодер реконструирует входной вектор в этом месте пространства. Кроме того, внутри автоэнкодера есть вектор латентного представления входных данных (как правило, низкой размерности), и если данные проецируются в латентном пространстве в область, ранее не задействованную при обучении, то, значит, и в обучающей выборке не было ничего похожего.

Существует ряд замкнутых и в чем-то обособленных работ:
1) Alain, G. and Bengio, Y. What regularized autoencoders learn from the data generating distribution. 2013.
2) Kamyshanska, H. 2013. On autoencoder scoring
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservativeness of Untied Auto-Encoders

В первой приводится обоснование того, что результат реконструкции Denoising автоэнкодеров связан с функцией плотности вероятности входных данных, но на автоэнкодеры накладывается ряд ограничений. Во второй приводятся достаточные требования к автоэнкодеру — веса энкодера и декодера должны быть «связаны», т.е. весовая матрица слоя энкодера — это транспонированая матрица декодера. В последней работе более полно исследуются необходимые и достаточные условия того, что автоэнкодер связан с плотностью вероятности.

Эти работы строго обосновывают теоретический базис связи автоэнкодеров с плотностью распределения обучающих данных. В прикладных задачах часто не требуется столь серьезного анализа, поэтому ниже по тексту будет приведен несколько иной подход, позволяющий оценить функцию плотности вероятности входных данных за счет ранее обученного автоэнкодера.

Пример на MNIST

В еще более ранних работах предлагалась эмпирическая идея, что для задачи классификации можно обучить автоэнкодеры по количеству классов (обучая каждый из них лишь на соответствующих ему подвыборке). И выбрать в качестве ответа тот класс и автоэнкодер, который дает минимальную невязку между входным изображением и реконструированным. Это было не сложно проверить на MNIST: обучить 10 автоэнкодеров (для каждой цифры), посчитать точность, а затем сравнить с аналогичной многослойной моделью классификатора.

Скрипты для обучения и тестирования на git-е (train_ae.py, calc_codes.py, calc_acc.py)

Архитектура и количество весов:

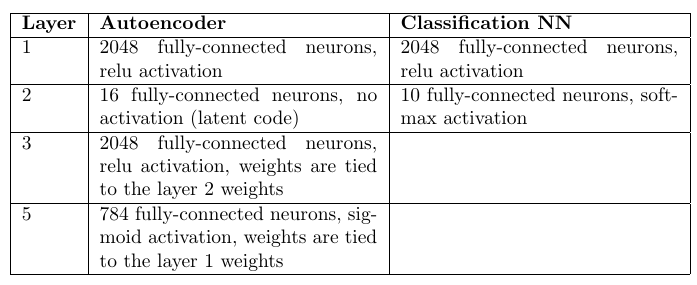
Автоэнкодеры: 98.6%
Классификатор на многослойном перцептроне: 98.4%

Внимательный читатель заметит, что весов в автоэнкодерах было в 10 раз больше (по их количеству). Однако, 10ти кратное увеличение количества весов в скрытом слое в многослойном перцептроне лишь ухудшает статистику.

Конечно, сверточные сети дают куда более высокую точность, но задача стояла лишь сравнить подходы при прочих равных.

В итоге можно отметить, что подход с автоэнкодерами вполне конкурентен полносвязанным сетям. И, хотя время на оптимизацию весов затрачивается значительно больше, он обладает одним важным преимуществом: способность детектировать аномалии во входных данных. Если ни один из автоэнкодеров не смог точно реконструировать входное изображение, то можно констатировать, что на вход попало аномальное изображение, которое не встречалось в обучающей выборке. Строго говоря, реконструировать можно изображение и не из входной выборки, но что делать в такой ситуации будет показано далее.

Рассмотрим одиночный автоэнкодер

Можно и несколько иным способом, чем в приведенных выше работах, провести качественный анализ связи плотности вероятности входных данных p(x) и отклика автоэнкодера.

Автоэнкодер — последовательное применение функции энкодера $$ и декодера $$, где $$ — входной вектор, а $$ — латентное представление. В некотором подмножестве входных данных (обычно близкое к обучающему) $$, где $$ — невязка. Невязку примем Гаусовским шумом (его параметры можно оценить после обучения автоэнкодера). В итоге делается ряд достаточно сильных предположений:

1) невязка — Гаусовский шум
2) автоэнкодер уже «натренирован» и работает

Но, что важно, на сам автоэнкодер не будет накладываться почти никаких ограничений.

Далее можно получить качественную оценку плотности вероятности p(x), на основании которой можно сделать несколько очень важных в дальнейшем выводов.

Оценка p(x) для одиночного автоэнкодера

Плотность распределения для $$ и $$ связаны следующим образом:

$$

Нам нужно получить связь p(x) и p(z). Для некоторых автоэнкодеров p(z) задается на стадии их тренировки, для других p(z) получить все же проще за счет меньшей размерности Z.

Плотность распределения невязки n известна, значит:

$$

$$ — это дистанция между x и его проекцией x*. В некоторой точке z* эта дистанция достигнет своего минимума. В этой точке частные производные аргумента экспоненты в формуле (2) по $$ (осям Z) будут нулевые:

$$

Здесь $$ скаляр, тогда:

$$

Выбор точки z*, где дистанция $$ минимальна, обусловлен процессом оптимизации автоэнкодера. Во время обучения именно квадратичная невязка и минимизируется (как правило): $$, где $$ — веса автоэнкодера. Т.е. после обучения g(x) стремится к z*.

Также мы можем разложить $$ в ряд Тейлора (до первого члена) вокруг z*:

$$

Так, теперь уравнение (2) станет:

$$

$$

$$

Заметьте, что последний множитель равен 1 из-за выражения (3). Первый множитель можно будет вынести за знак интеграла (он не содержит z) в (1). А также предположим, что p(z) достаточно гладкая функция и не сильно меняется в окрестности z*, т.е. заменим p(z)->p(z*).

После всех предположений интеграл (1) имеет оценку:

$$

где $$
Последний интеграл — n-мерный интеграл Эйлера-Пуассона:

$$

В итоге мы получили финальную оценку p(x):

$$

Вся эта математика была нужна, чтобы показать, что p(x) зависит от трех факторов:

• Дистанции между входным вектором и его реконструкцией, чем хуже восстановили — тем меньше p(x)
• Плотности вероятности p(z*) в точке z*=g(x)
• Нормировки функции p(z) в точке z*, которая рассчитывается для автоэнкодера из частных производных функции f

И еще от нормировочной константы, которая впоследствии будет отвечать за априорную вероятность выбора автоэнкодера для описания входных данных.

Несмотря на все допущения, результат получился весьма осмысленным и полезным с точки зрения вычислений.

Процедура классификации или оценки параметров

Теперь можно точнее описать процедуру классификации с использованием набора автоэнкодеров:

1. Обучение независимых автоэнкодеров для каждого класса на соответствующих выходных данных
2. Расчет матрицы W для каждого автоэнкодера
3. Оценка p(z) для каждого автоэнкодера

И для каждого входного вектора можно оценить теперь $$ по количеству классов. А это и будет функцией правдоподобия, которая необходима для принятия решения в рамках Байесовского правила принятия решений.

Точно также можно оценивать и неизвестные параметры, разбив пространство параметров на дискретные значения, обучив для каждого значения свой автоэнкодер. А затем, на основании лучшей Байесовской оценки, выбрать то значение, которое дает максимум функции правдоподобия.

Тут стоит заметить, что, формально, задача оценки p(z) ничуть не проще оценки p(x). Но на практике это не так. Пространство Z обычно имеет сильно меньшую размерность, либо вообще распределение задается при оптимизации весов автоэнкодера.

Идея объединения латентного пространства автоэнкодеров

Существует любопытная трактовка, предложенная Алексеем Редозубовым и описанная в следующих статьях:

1. An Artificial Neural Network Architecture Based on Context Transformations in Cortical Minicolumns. Vasily Morzhakov, Alexey Redozubov
2. Holographic Memory: A novel model of information processing by Neural Microcircuits. Alexey Redozubov, Springer
3. Совсем не нейронные сети. Моржаков В.

Информация может иметь совершенно различную трактовку в разных контекстах. Модель «набора автоэнкодеров» перекликается с этой предложенной идеей. Любой автоэнкодер — это латентная модель входных данных в рамках одного контекста (одного класса или иных фиксированных параметров), т.е. латентный вектор — трактовка, а каждый автоэнкодер — контекст. При поступлении входной информации она рассматривается в каждом контексте (каждым автоэнкодером), и выбирается тот контекст, который наиболее вероятен с учетом существующих моделей в каждом автоэнкодере.

Следующим разумным шагом будет допустить существование пересечения трактовок в различных контекстах. Т.е. при обучении мы часто знаем, что трактовка остается прежней, но форма представления (контекст) меняется. Например, ориентация объекта меняется, но объект остается прежним. Вектор описания объекта должен сохраняться, а контекст — ориентация меняется.

Тогда, если мы взглянем на формулу (4), то множитель p(z) оказывается можно оценивать для всего набора автоэнкодеров, а не для каждого в отдельности. Трактовка (латентный вектор) будет иметь общее распределение. Для небольшого количества автоэнкодеров это может не иметь значительной роли, но в реальной задаче это количество может быть огромным. Например, если определить по одному контексту на каждую возможную ориентацию 3D объекта, их может оказаться сотни тысяч. Теперь каждый пример, представленный для обучения в любом контексте, будет формировать распределение p(z).

Взаимозаменямость трактовки и контекста

В прикладной задаче сразу встанет вопрос: что назначить трактовкой, а что контекстом? Контекст и трактовка могут легко меняться местами, и никто не исключает существование возможности одновременного параллельного функционирования пары «наборов автоэнкодеров».

Для наглядности можно предложить такой пример:

Входное изображение содержит лица людей.
1) контекст — ориентация лица. Тогда для реконструкции входного изображения нам не хватает «трактовки» — кода, идентифицирущего лицо, который будет содержать в себе описание лица, прически, его освещения. При обучении нам нужно будет предъявлять одно и то же лицо с разных сторон, «замораживая» латентный код, меняя при этом ориентацию.
2) контекст — тип лица, освещения, прически. Тогда для реконструкции входного изображения нам не хватает ориентации лица. При обучении нужно будет предъявлять разные лица при разном освещении, но одной и той же ориентации.

Оптимальное Байесовское решение в первом случае будет приниматься относительно ориентации лица, а во втором — его типа. Предположительно, первый вариант даст лучшую точность по ориентации, а второй точнее оценит, чье это было лицо.

Обучение набора автоэнкодеров с общим латентным простраством

При обучении нам нужно знать, как одна по смыслу сущность выглядит в разных контекстах. Например, если говорить об изображении цифр и контексте-ориентации, то схематично такое кросс-обучение выглядит так:

Используется энкодер одного автоэнкодера, затем латентный код декодируется декодером другого автоэнкодера. Функция потерь при обучении остается стандартной. Интересно то, что если автоэнкодер выбран симметричным (т.е. веса энкодера и декодера связаны), то в каждой итерации оптимизируются все веса обоих автоэнкодеров.

Наиболее удобно для такого хитрого обучения подошел PyTorch, который позволяет делать достаточно сложные схемы обратного распространения ошибок, в том числе и динамические.

Стандартные шаги обучения каждого автоэнкодера чередуются с итерациями кросс-обучения. В результате у всех автоэнкодеров получается общее латентное пространство или связывается «трактовка» в различных контекстах.

Очень важно то, что в результате такого анализа мы сможем разделить входную информацию на «контекст» и «трактовку».

Пример обучения

Рассмотрим достаточно простой пример, основанный на MNIST, который поможет продемонстрировать принцип обучения автоэнкодеров с общим латентным пространством. В результате, на этом примере будет продемонстрировано формирование абстрактного понятия «куб» с помощью механизма, описываемого в статье.

На грани куба нанесены цифры из MNIST и он вращается вокруг одной из своих осей:

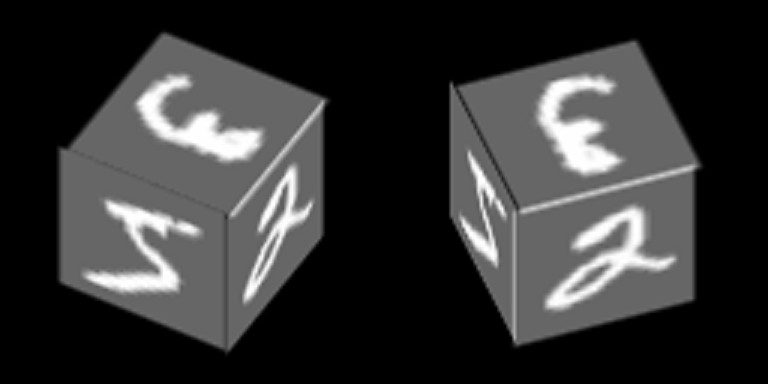
Будем обучать автоэнкодеры восстанавливать грани, контекст — ориентация грани.

Вот пример цифры «ноль» в 100 контекстах, первые 34 из которых соответствуют разным углам поворота боковой грани, а оставшиеся 76 — различные углы поворота верхней грани.

Мы предполагаем, что для каждого из этих 100 изображений «трактовки» должны быть одинаковые, и именно случайные их парасочетания используются для кросс-обучения.

После обучения вышеописанным методом удалось достичь того, что латентный код одного из автоэнкодеров можно декодировать другими автоэнкодерами, получив действительно осмысленное контекстное преобразование.

Например, на данном изображении показано, как результат кодирования автоэнкодера под номером 10 декодируется другими автоэнкодерами для одной из цифр:

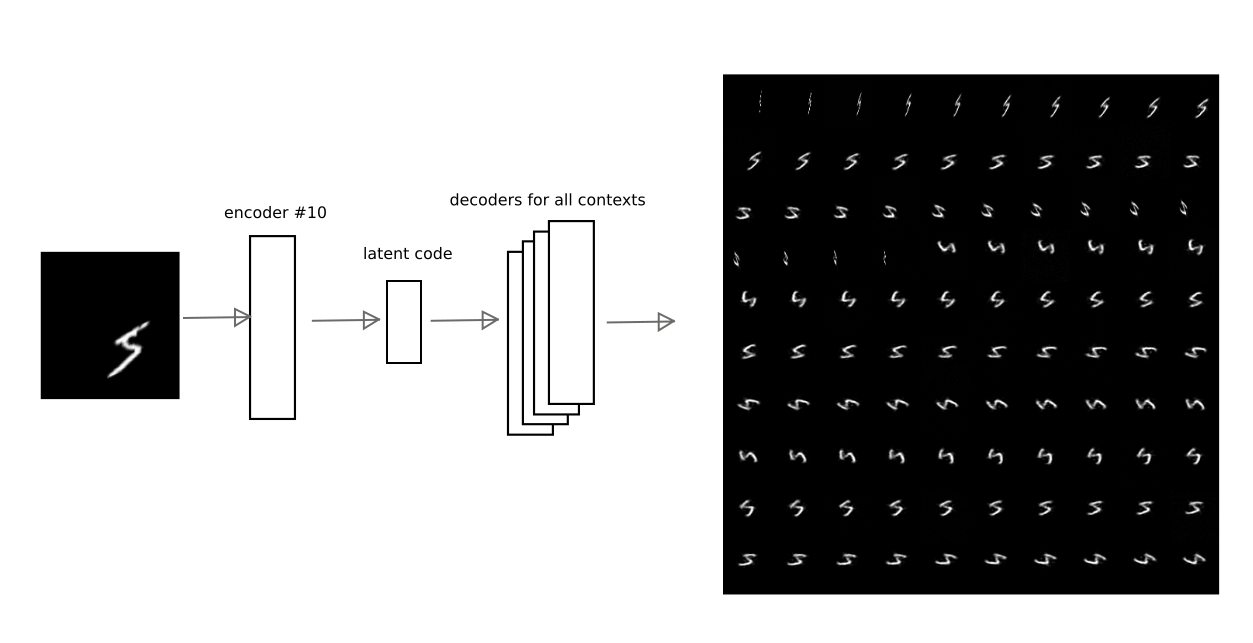
Таким образом, имея код «трактовки», т.е. латентный вектор автоэнкодера, можно восстановить исходное изображение в любом из обученных контекстов (т.е. декодером любого автоэнкодера).

Маскировка входного вектора

В формуле (4) везде фигурирует дисперсия невязки $$, которая выбрана константой для любого из компонентов входного вектора. Однако, если какие-то компоненты не имеют никакой статистической связи с латентной моделью, то дисперсия наверняка окажется значительно выше именно по этим компонентам. Дисперсия везде оказывается в знаменателе, а, значит, чем больше невязка, тем меньше вклад ошибки по компоненте. Можно отнестись к этому, как к маскировке некоторой части входного вектора.

Для данного примера с вращающимися гранями маска очевидна — проекция грани в конкретном контексте.

В упрощенном подходе в этом примере, который использует только невязку между входным изображением и реконструкцией, нужно лишь умножить невязку на маску для каждого из контекстов.

В общем случае, нужно строже оценивать параметры распределения, таким образом не вводя маски ручным образом.

Отделение трактовки от контекста

Отделив трактовку от контекста, можно получать абстрактные понятия. В обученном примере интересно продемонстрировать 2 эффекта:

1) one-shot learning, т.е. обучение со сверхмалым количеством примеров (в пределе одним).

Если анализировать лишь трактовку, игнорируя контекст, то становится возможным узнать новый образ в разных ориентациях грани, когда новый образ демонстрировался лишь в одной из ориентаций.

Тут важно заметить, что образ необходимо предъявить новый. Для корректности также зададимся целью запомнить не один образ, а научиться разделять 2 новых образа, не встречающихся ранее в тренировочной базе MNIST. Например, такие:

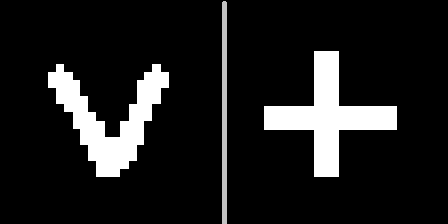
Задумка следующая: показать эти знаки в одном из геометрических контекстов (например, под номером 10), выбрать гиперплоскость, проходящую равноудаленно от трактовок этих знаков, а затем убедиться, что с помощью этой гиперплоскости мы сможем распознать, что за знак нам предъявлен при вращении грани (других контекстах).

Тут важно заметить, что автоэнкодеры не будут обучаться на новых знаках. За счет того разнообразия цифр, что есть в MNIST, можно предсказать, как будет выглядеть новый знак, который ранее не встречался, в различных контекстах.

Так знак V будет выглядеть после кодирования в контексте №10 и декодирования в оставшихся:

Видно, что предсказание не идеально, но визуально узнаваемо.

Обозначим эту демонстрацию «эксперимент 1» и опишем результат ниже.

2) а с кубом интересно продемонстрировать, что будет, если проигнорировать содержимое латентного вектора, а передать лишь степень правдоподобия каждого автоэнкодера.

Посмотрим как выглядит степень правдоподобия по каждому из контекстов для двух кубов с совершенно разной текстурой (цифры 5 и 9) для 100 контекстов, которые можно отобразить как карту:

Видно, что карты довольно похожи, несмотря на различную текстуру на сторонах куба.

Т.е. сам вектор, содержащий правдоподобие моделей автоэнкодеров (контекстов), позволяет сформулировать новое абстрактное понятие, связанное с 3х-мерной формой куба. Этот вектор также может описываться на следующем уровне автоэнкодером, который обучается модели куба.

Во втором эксперименте нужно будет создать второй уровень обработки информации, в котором обучить автоэнкодер абстрактной модели куба. А, затем, с помощью обратной проекции восстановить исходное изображение для разных реализаций модели этого куба. Проще говоря, заставить куб вращаться.

Результат «эксперимента №1»

Обученный на MNIST набор автоэнкодеров применяется к двум новым изображениям, предъявленным в контексте №10. Получаются 2 точки в латентном пространстве, соответствующие знакам V и +. Зададим плоскость, равноудаленную от обеих точек, которую будем использовать для принятия решения. Если точка находится с одной стороны от плоскости — знак V, с другой — знак «плюс».

Теперь получим коды преобразованных изображений и для каждого из них рассчитаем дистанцию до плоскости, сохранив знак.

В итоге удается различить, что же за знак был предъявлен для всех 100 контекстов.

Распределение дистанций на графике:

Визуализация результата на примере отдельных символов:

Т.е. латентные коды знаков V в абсолютно разных контекстах значительно ближе друг другу в латентном пространстве, чем коды V и знака плюс в одном и том же контексте. За счет этого в 100 из 100 случаев и удается успешно различить знаки во всевозможных ориентациях граней куба, несмотря на то, что предъявлялся лишь один образец каждого знака.

Удалось продемонстрировать классический «one-shot learning», который невозможен в исходной архитектуре искусственных нейронных сетей. Основной принцип, за счет которого этот подход работает, очень похож на «transfer learning», продемонстрированный, например, в этой статье.

Ссылка на git (train_ae_shared.py, test_AB.py)

Результат «эксперимента №2»

Отделение трактовки от контекста также позволяет обучаться на ограниченном наборе примеров. Возможно демонстрировать лишь одну из возможных трактовок в различных контекстах (зафиксировав «латентный вектор»). Абстрактную модель куба как раз можно получить, демонстрируя лишь одну цифру на всех гранях.

Эксперимент построен следующим образом:

1. Подготавливается обучающая база: кубы с градусом поворота от 0 до 90 градусов. На гранях кубах изображена цифра 5.
2. Вектор правдоподобия контекстов, отделенный от трактовки (латентного кода), передается на следующий уровень, где обучается автоэнкодер, ответственный за модель куба
3. Затем делаем обратную проекцию: для каждой вероятной точки латентного пространства автоэнкодера, ответственного за абстракцию «куб», мы можем рассчитать вектор правдоподобия контекстов на первом уровне, доопределить латентный код знака на грани и построить исходное изображение, которое, возможно, никогда не встречалось нам в обучающей выборке.

Обучающая выборка состояла из 5421 изображений с изображением цифры 5 на сторонах, пример:

кубы с поворотом от 0 до 90 градусов

Мы заранее знаем, что куб имеет только одну степень свободы вращения, поэтому автоэнкодер на втором уровне имеет лишь одну компоненту в латентном коде. После обучения можно варьировать эту компоненту от 0 до 1 (функция активации латентного слоя была выбрана сигмоид) и видеть, какой вектор правдоподобия контекстов воспроизводится при декодировании:

Затем этот вектор передается на уровень 1, в котором 100 контекстов ориентаций граней, выбираются локальные максимумы и «воображается» любой латентный код знака на гранях куба. «Вообразим» цифру 3 на гранях, меняя латентный вектор в автоэнкодере, ответственном за абстрактное понятие куб, и получим следующее изображение куба:

Или код знака V, который вообще не встречался в обучающей выборке:

Качество хуже, но знак узнаваем.

Таким образом, на втором уровне обработки изображений мы получили автоэнкодер, который моделирует разнообразие абстрактного понятия «куб». На практике же, в задачах распознавания принцип обратной проекции, показанный в эксперименте, крайне важен, т.к. позволяет устранить неоднозначности трактовки за счет формирования абстрактных понятий более высокого уровня.

Ссылка на git (second_level.py, second_level_test.py)

Другие примеры, когда отделение контекста работает

В предыдущей моей статье при распознавании автомобильных номеров аналогичный метод применялся без объяснения. Положение, ориентация и масштаб цифры на изображении отделялись от содержимого, следующий уровень воспринимал эти данные для построения модели «автомобильный номер». Не важно какие цифры, важна их взаимная геометрическая конфигурация, чтобы мы могли уверенно говорить о том, что это автомобильный номер (кстати, тоже абстрактное понятие).

По аналогии можно привести ряд других примеров из компьютерного зрения: 3D форма объекта или его контуры отделимы от его текстуры и фона; перечисление составных частей в отрыве от взаимной пространственной конфигурации тоже часто позволяет сформировать новое абстрактное понятие.

Также интересно то, как в других областях машинного обучения это может работать: выделение мелодии песни — это тоже отказ от трактовки (какая конкретно гласная произносится) и использование только контекста (высота основного тона); грамматические конструкции (формирование паттернов, например,«кто-то сделал что-то»).

Обсуждение проблемы сильного ИИ

В настоящий момент сложно сформулировать, чем же отличается сильный ИИ от слабого. Вероятно, в этот список стоит включить все то, чего не хватает существующим подходам и алгоритмам для того, чтобы вычислительные машины действовали так же эффективно, как человек, например:

• Принятие решений, использование стратегий, решение в условиях неопределенности. Именно высокая неопределенность требует выбирать наилучшую из сформулированных за время обучения моделей
• Отражение моделей окружающего физического и социального мира, в том числе самосознания и сознания окружающих
• Механизмы абстрактного мышления, позволяющие формулировать понятия, которые возможно использовать на широком многообразии входных данных впоследствии
• Способность к «расшифровке» собственных мыслей

Также явно не хватает развитых механизмов памяти, интегрированных с процессом обучения, механизмов поощрения/наказания.

В статье продемонстрирован подход к задаче распознавания и оценки параметров, который основан на выборе наилучшей модели, описывающей входные данные. Предполагается, что это и есть механизм выбора наилучшей трактовки и контекста. За счет разделения трактовки и контекста на выходе модуля (набора автоэнкодеров), можно формулировать абстрактные понятия или обобщать опыт в отрыве от контекста, благодаря этому уменьшать обучающую выборку. Наборы контекстов могут отражать показания датчиков машины (ориентация, положение, скорость и др.), за счет чего становится возможным естественное обучение без учителя.

Кроме того, несмотря на то, что при обучении автоэнкодеров используется Deep learning, процессы, происходящие в автоэнкодерах, легко анализируются на каждом уровне обработки информации, т.к. можно определить, в рамках какой модели (или в каком контексте) была найдена наилучшая трактовка. А смысл обратных связей между уровнями, которые нужно вводить в сложных системах, — повышение или понижение вероятности выбора того или иного контекста.

Результат

Предложен математический аппарат, на основании которого можно выбирать ту или иную модель, описывающую входные данные, руководствуясь Байесовским решающим правилом. Модели получаются с помощью автоэнкодеров с общим латентным пространством. Предложена идея, согласно которой латентный код автоэнкодера — трактовка, а латентная модель, т.е. сам автоэнкодер, — контекст.

Продемонстрировано, что набор автоэнкодеров сам по себе не уступает по точности полносвязным искусственным нейронным сетям на примере MNIST.

Показан эффект от отделения трактовки от контекста: минимизация необходимого набора данных (в пределе «one-shot learning») для распознавания вновь предъявленных образов за счет предобучения на других данных.

Показан эффект от отделения контекста от трактовки: возможность формирования абстрактных понятий следующего уровня на примере геометрической абстракции «куб».

Ссылки

1) Alain, G. and Bengio, Y. What regularized autoencoders learn from the data generating distribution. 2013.
2) Kamyshanska, H. 2013. On autoencoder scoring
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservativeness of Untied Auto-Encoders
4) An Artificial Neural Network Architecture Based on Context Transformations in Cortical Minicolumns. Vasily Morzhakov, Alexey Redozubov
5) Holographic Memory: A novel model of information processing by Neural Microcircuits. Alexey Redozubov, Springer
6) Совсем не нейронные сети. Моржаков В.
7) en.wikipedia.org/wiki/Gaussian_integral
8) Adversarial Examples: Attacks and Defenses for Deep Learning
9) One-Shot Imitation Learning

P.S:
Это статья — русскоязычный электронный препринт, опубликованный для обсуждения результатов, поиска ошибок. Приветствуется любая конструктивная критика!