Как сделать ещё больше некорректных состояний ещё более невыразимыми

Не так давно на Хабре перевели статью о том, как при помощи алгебраических типов данных добиться того, чтобы некорректные состояния были невыразимыми. Сегодня мы посмотрим на чуть более обобщённый, масштабируемый и безопасный способ выражать невыразимое, а поможет нам в этом хаскель.

Если вкратце, в той статье рассматривается некоторая сущность с почтовым адресом и электронным адресом, а также с дополнительным условием, что должен быть хотя бы один из этих адресов. Как предлагается выразить это условие на уровне типов? Предлагается записывать адреса так:

type ContactInfo =      | EmailOnly of EmailContactInfo     | PostOnly of PostalContactInfo     | EmailAndPost of EmailContactInfo * PostalContactInfo

Какие у этого подхода есть проблемы?

Самая очевидная (и её несколько раз отмечали в комментах к той статье) — этот подход совсем не масштабируем. Представим, что у нас не два типа адресов, а три или пять, и условие корректности выглядит как «должен быть либо почтовый адрес, либо одновременно электронный адрес и адрес в офисе, и при этом не должно быть нескольких адресов одного типа». Написать соответствующий тип желающие могут в качестве упражнения для самопроверки. Задание со звёздочкой — переписать этот тип на случай, когда условие про отсутствие дубликатов пропало из ТЗ.

Разделяем

Как можно решить эту проблему? Давайте попробуем пофантазировать. Только сначала проведём декомпозицию и будем разделять класс адреса (например, почтовый/емейл/номер стола в офисе) и соответствующее этому классу содержимое:

data AddrType = Post               | Email               | Office

Про содержимое пока думать не будем, ибо про него в ТЗ на условие валидности списка адресов ничего нет.

Если бы мы проверяли соответствующее условие в рантайме какого-нибудь конструктора какого-нибудь обычного ООП-языка, то мы бы просто написали функцию вроде

valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs  -- не делайте так в продакшене                hasPost = Post `elem` xs                 hasEmail = Email `elem` xs                hasOffice = Office `elem` xs            in hasNoDups && (hasPost || (hasEmail && hasOffice))

и кидали бы какой-нибудь экзепшн, если она возвращает False.

Можем ли мы вместо этого проверять аналогичное условие при помощи тайпчекера, при компиляции? Оказывается, что да, можем, если система типов языка достаточно выразительна, и остаток статьи мы будем ковырять этот подход.

Здесь нам очень помогут зависимые типы, а так как самый адекватный способ писать завтипизированный код на хаскеле — это сначала написать его на агде или идрисе, мы резко переобуемся и будем писать на идрисе. Синтаксис идриса достаточно близок к хаскелю: например, у вышеупомянутой функции нужно лишь немного поменять сигнатуру:

valid : List AddrType -> Bool

Теперь вспомним, что кроме классов адресов нам нужно ещё их содержимое, и закодируем зависимость полей от класса адреса как GADT:

data AddrFields : AddrType -> Type where   PostFields : (city : String) -> (street : String) -> AddrFields Post   EmailFields : (email : String) -> AddrFields Email   OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office

То есть, если нам дано значение fields типа AddrFields t, то мы знаем, что t — это некоторый клсас AddrType, и что в fields лежит соответствующий именно этому классу набор полей.

addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields

Что такое весь адрес целиком в данной модели? Это пара из класса адреса и соответствующих полей:

Addr : Type Addr = (t : AddrType ** AddrFields t)

Любители теории типов скажут, что это экзистенциальный зависимый тип: если нам дано некоторое значение типа Addr, то это значит, что существует значение t типа AddrType и соответствующий этому t набор полей AddrFields t. Естественно, адреса различного класса имеют один и тот же тип:

someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro")  someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762)

Более того, если нам даны поля EmailFields, то единственный класс адреса, который подходит — Email, поэтому его можно не указывать, тайпчекер выведет его сам:

someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro")  someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762)

Напишем вспомогательную функцию, которая по списку адресов даёт соответствующий список классов адресов, и сразу её обобщим до работы над произвольным функтором:

types : Functor f => f Addr -> f AddrType types = map fst

Здесь экзистенциальный тип Addr ведёт себя как привычная пара: в частности, можно попросить её первый компонент AddrType (задание со звёздочкой: почему попросить второй компонент так не получится?).

Поднимаем

Теперь мы переходим к ключевой части нашего повествования. Итак, у нас есть список адресов List Addr и некоторый предикат valid : List AddrType -> Bool, выполнение которого для данного списка мы хотим гарантировать на уровне типов. Как их нам совместить? Конечно же, ещё одним типом!

data ValidatedAddrList : List Addr -> Type where   MkValidatedAddrList : (lst : List Addr) ->                         (prf : valid (types lst) = True) ->                         ValidatedAddrList lst

Теперь будем разбирать, что мы тут понаписали.

data ValidatedAddrList : List Addr -> Type where означает, что тип ValidatedAddrList параметризуется, собственно, списком адресов.

Посмотрим на сигнатуру единственного конструктора MkValidatedAddrList этого типа: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst. То есть, он принимает некоторый список адресов lst и ещё один аргумент prf типа valid (types lst) = True. Что значит этот тип? А значит он, что значение слева от = равно значению справа от =, то есть, что valid (types lst), собственно, равно True.

Как это работает? Сигнатура = выглядит как (x : A) -> (y : B) -> Type. То есть, = принимает два произвольных значения x и y (возможно, даже разных типов A и B, что означает, что неравенство в идрисе гетерогенное, и что несколько неоднозначно с точки зрения теории типов, но это тема для отдельной дискуссии). За счёт чего тогда демонстрируется равенство? А за счёт того, что единственный конструктор = — Refl с сигнатурой почти (x : A) -> x = x. То есть, если у нас есть значение типа x = y, то мы знаем, что оно было построено с использованием Refl (потому что других конструкторов нет), а значит, что x на самом деле равно y.

Отметим, что именно поэтому в хаскеле мы всегда будем в лучшем случае притворяться, что мы что-то там доказываем, потому что в хаскеле есть undefined, который населяет любой тип, поэтому вышеупомянутое рассуждение там не проходит: для любых x, y терм типа x = y мог быть создан через undefined (или через бесконечную рекурсию, скажем, что по большому счёту то же самое с точки зрения теории типов).

Отметим ещё, что равенство тут имеется в виду не в смысле хаскелевского Eq или какого-нибудь operator== на C++, а существенно более строгое: структурное, которое, упрощая, означает, что два значения имеют одну и ту же форму. То есть, обмануть его так просто не получится. Но вопросы равенства традиционно тянут на отдельную статью.

Дабы закрепить наше понимание равенства, напишем юнит-тесты на функцию valid:

testPostValid : valid [Post] = True testPostValid = Refl  testEmptyInvalid : valid [] = False testEmptyInvalid = Refl  testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl  testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl

Эти тесты хороши тем, что их даже запускать не надо, достаточно того, что тайпчекер их проверил. Действительно, давайте заменим True на False, например, в самом первом из них и посмотрим, что будет:

testPostValid : valid [Post] = False testPostValid = Refl

Тайпчекер ругнётся

как и ожидалось. Замечательно.

Упрощаем

Теперь немного отрефакторим наш ValidatedAddrList.

Во-первых, паттерн сравнения некоторого значения с True достаточно распространён, поэтому в идрисе для этого есть специальный тип So: можно воспринимать So x как синоним для x = True. Поправим определение ValidatedAddrList:

data ValidatedAddrList : List Addr -> Type where   MkValidatedAddrList : (lst : List Addr) ->                         (prf : So (valid $ types lst)) ->                         ValidatedAddrList lst

Кроме того, для So есть удобная вспомогательная функция choose, по смыслу поднимающая проверку на уровень типов:

> :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b))     Perform a case analysis on a Boolean, providing clients with a So proof

Нам она пригодится, когда мы будем писать функции, модифицирующие этот тип.

Во-вторых, иногда (особенно при интерактивной разработке) идрис может найти подходящее значение prf самостоятельно. Для того, чтобы в таких случаях не нужно было его конструировать руками, есть соответствующий синтаксический сахар:

data ValidatedAddrList : List Addr -> Type where   MkValidatedAddrList : (lst : List Addr) ->                         {auto prf : So (valid $ types lst)} ->                         ValidatedAddrList lst

Фигурные скобки означают, что это неявный аргумент, который идрис будет пытаться вытащить из контекста, а auto означает, что он его ещё и будет пытаться сконструировать сам.

Итого, что нам даёт этот новый ValidatedAddrList? А даёт оно такую цепочку рассуждений: пусть val — значение типа ValidatedAddrList lst. Это значит, что lst — некоторый список адресов, и, кроме того, val было создано при помощи конструктора MkValidatedAddrList, которому мы передали этот самый lst и ещё одно значение prf типа So (valid $ types lst), который почти valid (types lst) = True. А чтобы мы могли построить prf, нам нужно, собственно, доказать, что это равенство выполняется.

А самое прекрасное, что это всё проверяется тайпчекером. Да, выполнять проверку valid придётся в рантайме (потому что адреса могут читаться из файла или из сети), но тайпчекер гарантирует, что эта проверка будет сделана: без неё невозможно создать ValidatedAddrList. По крайней мере, в идрисе. В хаскеле можно, увы.

Вставляем

Чтобы убедиться в неизбежности проверки, попробуем написать функцию добавления адреса в список. Первая попытка:

insert : (addr : Addr) ->          ValidatedAddrList lst ->          ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst)

Неа, тайпчекер даёт по пальцам (хотя и не очень читабельно, издержки того, что valid слишком сложен):

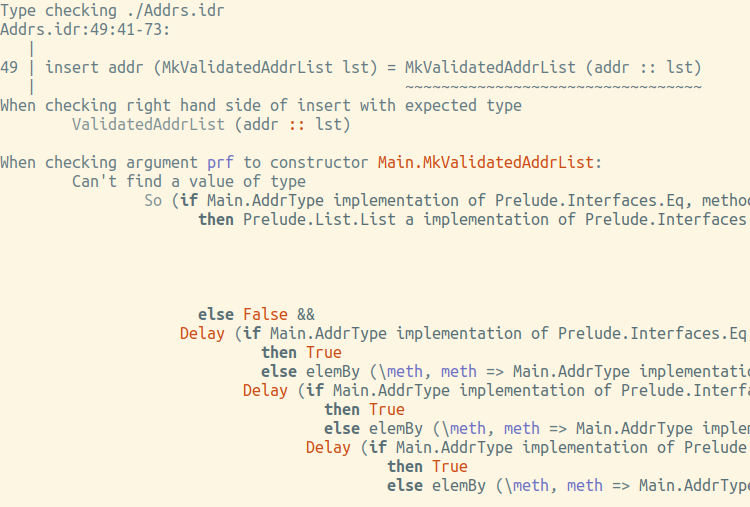
Как нам получить экземпляр этого вот So? Не иначе, как вышеупомянутым choose. Вторая попытка:

insert : (addr : Addr) ->          ValidatedAddrList lst ->          ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) =   case choose (valid $ types (addr :: lst)) of        Left l => MkValidatedAddrList (addr :: lst)        Right r => ?rhs

Это почти тайпчекается. «Почти» потому, что непонятно, что подставить вместо rhs. Вернее, понятно: в этом случае функция должна как-то сообщить об ошибке. Значит, надо поменять сигнатуру и завернуть возвращаемое значение, например, в Maybe:

insert : (addr : Addr) ->          ValidatedAddrList lst ->          Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) =   case choose (valid $ types (addr :: lst)) of        Left l => Just $ MkValidatedAddrList (addr :: lst)        Right r => Nothing

Это тайпчекается и работает как надо.

Но теперь возникает следующая не очень очевидная проблема, которая была, на самом деле, и в исходной статье. Тип этой функции не мешает написать такую реализацию:

insert : (addr : Addr) ->          ValidatedAddrList lst ->          Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing

То есть, мы всегда говорим, что не смогли построить новый список адресов. Тайпчекается? Да. Корректно? Ну, вряд ли. Можно ли этого избежать?

Оказывается, что можно, и у нас есть весь нужный для этого инструментарий. В случае успеха insert возвращает ValidatedAddrList, который содержит в себе доказательство этого самого успеха. Так добавим элегантную симметрию и попросим функцию возвращать ещё и доказательство неудачи!

insert : (addr : Addr) ->          ValidatedAddrList lst ->          Either            (So (not $ valid $ types (addr :: lst)))            (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) =   case choose (valid $ types (addr :: lst)) of        Left l  => Right $ MkValidatedAddrList (addr :: lst)        Right r => Left r

Теперь мы не можем просто взять и всегда возвращать Nothing.

Аналогично можно поступить и для функций удаления адреса и тому подобных.

Посмотрим, как теперь это всё в итоге выглядит.

Попробуем создать пустой список адресов:

Нельзя, пустой список не является валидным.

Как насчёт списка из одного лишь почтового адреса?

Окей, попробуем вставить почтовый адрес в список, в котором уже есть почтовый адрес:

Попробуем вставить емейл:

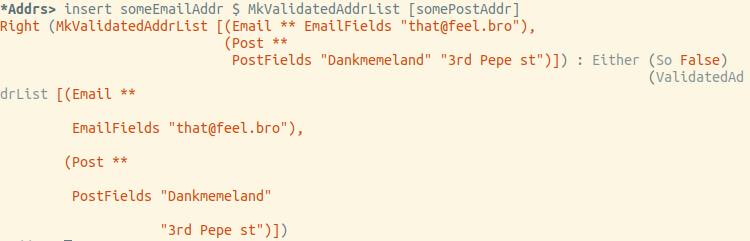
В итоге всё работает ровно так, как и ожидалось.

Ффух. Я думал, это будет на три строчки, но получилось чуть дольше. Так что исследовать, как далеко мы сможем зайти на хаскеле, мы будем в следующей статье. Ну а пока немного

Поразмышляем

В чём в итоге профит такого решения по сравнению с приведённым в статье, на которую мы сослались в самом начале?

1. Оно, опять же, куда более масштабируемо. Сложные функции валидации писать легче.
2. Оно более изолировано. Клиентский код вообще не обязан знать, что там внутри функции валидации, тогда как форма ContactInfo из оригинальной статьи требует на это завязываться.
3. Логика валидации пишется в виде обычных и привычных функций, так что её можно сразу проверить вдумчивым чтением и протестировать компилтайм-тестами, а не выводить смысл проверки из формы типа данных, представляющих уже проверенный результат.
4. Становится возможным чуть более точно специфицировать поведение функций, работающих с интересующим нас типом данных, особенно в случае непрохождения проверки. Например, написанный в итоге insert просто невозможно написать неправильно. Аналогично можно было бы написать insertOrReplace, insertOrIgnore и тому подобные, поведение которых полностью специфицировано в типе.

В чём профит по сравнению ООП-решением в таком духе?

class ValidatedAddrListClass { public:     ValidatedAddrListClass(std::vector<Addr> addrs)     {         if (!valid(addrs))             throw ValidationError {};     } };

1. Код более модуляризован и безопасен. В случае выше проверка — это действие, которое проверяется один раз, и про которое потом забыли. Держится всё на честном слове и договорённости, что если у вас есть ValidatedAddrListClass, то его реализация когда-то там сделала проверку. Сам факт этой проверки из класса как некоторое значение выковырять никак нельзя. В случае же значения некоторого типа это значение можно передавать между разными частями программы, использовать для построения более сложных значений (например, опять же, отрицания этой проверки), исследовать (см. следующий пункт) и вообще делать всё то же, что мы привыкли делать со значениями.
2. Такие проверки можно использовать при (зависимом) паттерн-матчинге. Правда, не в случае этой функции valid и не в случае идриса, она больно сложновата, а идрис больно туповат, чтобы из структуры valid можно было извлечь полезную для паттернов информацию. Тем не менее, valid можно переписать в чуть более дружественном к паттерн-матчингу стиле, но это выходит за рамки данной статьи и вообще само по себе нетривиально.

В чём недостатки?

Я вижу лишь один серьёзный фундаментальный недостаток: valid — слишком глупая функция. Она возвращает всего один бит информации — прошли данные валидацию или нет. В случае более умных типов мы могли бы достичь кое-чего поинтереснее.

Например, представим себе, что из ТЗ пропало требование уникальности адресов. В этом случае очевидно, что добавление нового адреса к уже имеющемуся списку адресов не сделает список невалидным, поэтому можно было бы доказать эту теорему, написав функцию с типом So (valid $ types lst) -> So (valid $ types $ addr :: lst), и использовать её, например, для написания типобезопасного всегда успешного

insert : (addr : Addr) ->          ValidatedAddrList lst ->          ValidatedAddrList (addr :: lst)

Но, увы, теоремы любят рекурсию и индукцию, а в нашей задаче нет какой-то изящной индуктивной структуры, поэтому, на мой взгляд, код с дубовой булевой valid тоже неплох.