Добрый день!
Как и обещал в первой своей статье, я хочу ознакомить Вас с одним из методов решения системы диофантовых уравнений. Цель статьи ознакомить остальных читателей с этой методикой и донести её в более или менее понятном виде.
Рассмотрим систему из двух диофантовых уравнений
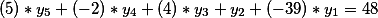
и

Найдем все возможные решения первого уравнения. Как, спросите Вы? Наверняка есть разные методики, но я поделюсь в одной из следующих статей, как бы я решал подобную задачу. А сейчас просто примем что общее решение имеет вид

Как проверить что я не лгу?
Достаточно вспомнить матричное исчисление и умножить вектор значений нашего первого диофантового уравнения(без свободного члена) на матрицу всех коэффициентов.

получили в результате значение свободного члена, а следовательно вычисления правильные
Следующим этапом мы подставим наше общее решение

во второе уравнение

Процедура такая же: умножаем вектор из коэффициентов второго уравнения на общее решение первого
получаем вот такой результат
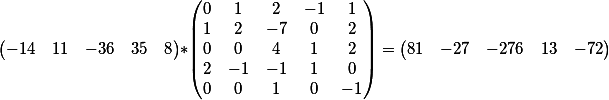
то есть мы получили уравнение вида
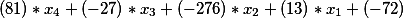
С правой стороны второго диофантового уравнения как был свободный член равный -335, так и остался, то есть наше окончательное решение на этом этапе имеет вид
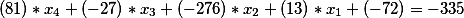
Или перенеся свободные члены в правую сторону получим
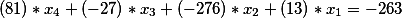
Итак, мы получили очередное диофантовое уравнение. Давайте найдем его общее решение и проверим его на истинность.

то есть общее решение имеет вид
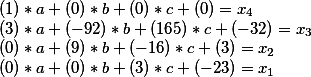
А теперь делаем обратное преобразование(пусть так называется). То есть в систему

Мы вместо неизвестных x подставляем то, что получилось на последнем этапе
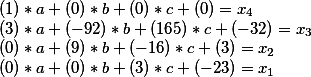
В матричном исчислении это решается умножением одной матрицы на другую.
Но с первой матрицей надо сделать определенную процедуру: убрать (временно) последний столбец с свободными членами, так как этот параметр не участвует в умножении, и будет пользоваться позднее.
Результат умножения двух матриц порождает
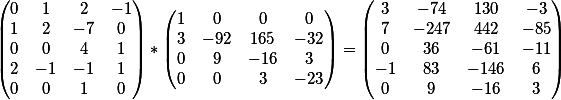
матрицу
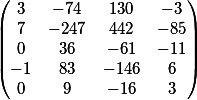
Последний столбец это свободные члены этой системы.
Учтем тот столбец который временно удаляли, перед умножением и сложим их
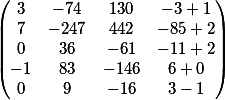
наш окончательный ответ в виде матрицы
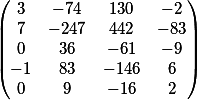
Проверим?
Векторное произведение коэффициентов первого уравнения и матрицы
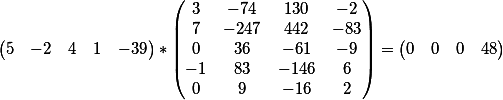
а векторное произведение коэффициентов второго уравнения и матрицы
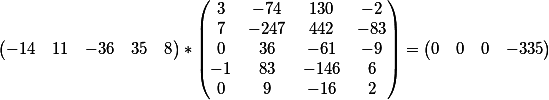
Как видим, результат совпадает с свободным членом каждого из уравнений.
Таким образом общее решение имеет вид
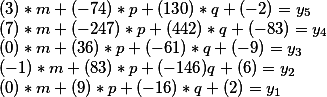
где m,p,q — могут принимать любые целые значения
Таким незамысловатым способом можно решать и более сложные линейные диофантовые уравнения. По следам этого алгоритма создан калькулятор правда, этот калькулятор очень не любит когда вместо значений в коэффициентах первого уравнения начальной системы встречаются нули. Но это проблема конкретной моей реализации этого алгоритма.
В следующей теме я расскажу как создавать диофантовые уравнения по матрице общего решения. Задача в общем то банальна и делается в одно действие, но вдруг кто то не знает.
Буду благодарен за замечания, отзывы и предложения.
ссылка на оригинал статьи https://habr.com/ru/post/484154/