Число Пи — пожалуй, самое знаменитое число в мире. Это единственное число, ради которого учредили особый день в году — День числа пи, отмечаемый 14 марта. В этой статье мы рассмотрим различные особенности числа π и попробуем с его помощью создать что-нибудь развлекательное, используя Python. Например арт-объекты, музыку, игры и другое. Открываем блокнот Colab и начинаем.
Colab и настройка среды
Введение в Colab
Google Colaboratory, или просто Colab, — это среда разработки на Python с использованием инструмента для разработки Jupyter Notebook, позволяющая подключаться к мощным облачным вычислительным ресурсам Google и запускать код Python. Colab формирует среду выполнения, в которой можно устанавливать пакеты, получать доступ к данным в онлайн-режиме, осуществлять навигацию по файловой системе, а также сохранять/восстанавливать данные.
Запуск кода в Colab
Ячейки бывают двух типов: кодовые и текстовые. В текстовых ячейках приводится описание действий, а кодовые ячейки можно запускать по отдельности, нажимая кнопку воспроизведения. Данный блокнот Colab содержит 12 разделов. Для запуска кода в определённой кодовой ячейке нажмите кнопку воспроизведения в левом верхнем углу этой ячейки.
Примечание: можно воспользоваться оболочкой Jupyter Notebook из репозитория GitHub.
Установите зависимости и загрузите файлы
В первом разделе устанавливаются все зависимости и клонируется мой репозиторий GitHub — так мы получим доступ к вспомогательному коду и текстовым файлам, содержащим цифры числа π. Эту ячейку необходимо запустить раньше всех других ячеек. Код этой ячейки загружает различные зависимости в среду Linux и устанавливает пакеты python, необходимые для запуска кода.
1. Что такое число пи?
Пи (π) — иррациональное число. Число называется иррациональным, если оно не может быть представлено в виде арифметической дроби, то есть его десятичное представление бесконечно, и группы цифр в его записи никогда циклично не повторяются. Другими словами, точного значения числа π мы не знаем и никогда не узнаем.
Кроме того, Пи является трансцендентным числом, то есть числом, которое не может являться ненулевым корнем многочлена с рациональными коэффициентами. По сути, такое число не является алгебраическим. Самые известные трансцендентные числа — π и e.
Определение значения π стало для математиков-энтузиастов растянувшейся на много веков забавой. В этой статье рассказывается о том, каких успехов с течением времени достигли математики в вычислении десятичных знаков числа π. Сегодня рекорд по количеству вычисленных знаков числа π (50 триллионов) принадлежит Тимоти Мулликану (Timothy Mullican). Он применил алгоритм многопоточного расчёта числа π «y-cruncher», разработанный Александром И (Alexander Yee), и это заняло у него 303 дня.
Несмотря на то что точное значение числа π нам не известно, его важность трудно переоценить — ведь оно незримо присутствует во всей нашей жизни. Число π определяется как отношение длины окружности к её диаметру; однако области, в которых используется это число, выходят далеко за рамки элементарной геометрии. Если интересно, можете посмотреть видео на YouTube-канале Numberphile (относительно старое), в котором довольно подробно разбираются интересные свойства числа π.
2. Сколько вам π-кратных лет?
Узнайте ваш π-кратный возраст. Укажите день рождения и определите свой возраст в π-кратных годах и днях.
3. Вычисление приближённого значения числа π

Рассчитайте приближённое значение числа π, задав количество элементов почленного суммирования. Для вычисления приближённого значения числа π используется формула Лейбница — бесконечный знакочередующийся ряд, медленно сходящийся к пределу π, см. формулу ниже.
Для запуска кода укажите количество элементов почленного суммирования (n), которое нужно использовать для вычисления приближённого значения числа π.
4. Миллион знаков числа π
Хотите узнать, как выглядит первый миллион знаков числа π в десятичной и в шестнадцатеричной системах счисления? Помните, что расчёт миллиона символов — это большая нагрузка на браузер, работа компьютера может замедлиться.Чтобы очистить окно вывода, после запуска ячейки щелкните значок «x» слева от окна вывода.
Один миллион десятичных цифр числа π
Один миллион шестнадцатеричных цифр числа π
5. График распределения цифр числа π

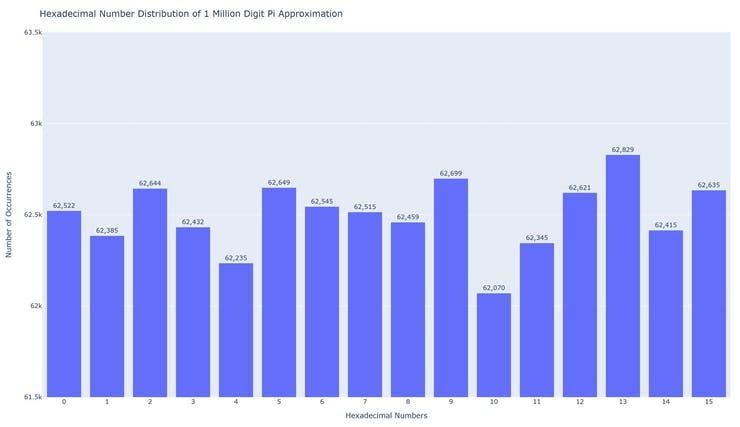
Возьмём первый миллион цифр числа π в десятичной и шестнадцатеричной системах счисления, построим диаграмму распределения цифр числа π и попробуем выяснить, есть ли в этом числе цифры, встречающиеся в первом миллионе цифр чаще, чем другие.
На первой диаграмме представлено распределение цифр числа π в десятичной, на второй — в шестнадцатеричной системе счисления. Диаграммы также записываются в папку «output» в виде web-страницы interactive.html, которую можно загрузить на вкладке file (файл) в левой части блокнота Colab. Диаграммы формируются с помощью функции построения столбчатых диаграмм библиотеки Plotly.
6. Хордовая диаграмма числа π
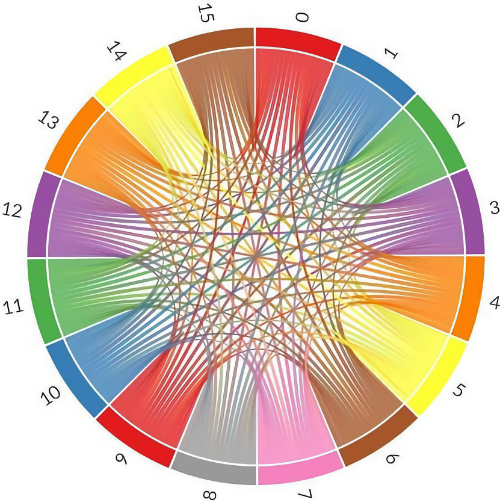
Хордовая диаграмма — особый вид кольцевой диаграммы, на которой отображаются дуги, соединяющие один узел с другим. В нашем примере дуги соединяют между собой последовательные цифры числа π. Узлов столько, сколько всего существует цифр (от 0 до 9 — для десятичной и от 0 до 15 — для шестнадцатеричной системы счисления). Дуги отображают переходы от одной цифры к другой. Например, первые цифры после запятой в числе π: «14159». Начинаем от 1 и рисуем дугу к 4, затем рисуем дугу от 4 к 1, затем дугу от 1 к 5, затем дугу от 5 к 9 и так далее.
Первый рисунок — это хордовая диаграмма первого миллиона десятичных цифр числа π. Второй — хордовая диаграмма первого миллиона шестнадцатеричных цифр числа π. Диаграммы также записываются в папку «output» в виде web-страницы interactive.html, которую можно загрузить на вкладке file (файл) в левой части блокнота Colab. Хордовые диаграммы генерируются с помощью модуля Chord.
7. Змейка — пи-версия
Сыграем в пи-версию Змейки? Я доработал игру таким образом, чтобы змейку можно было двигать в направлении различных цифр числа π. У меня змейка заглатывает не яблоки, а десятичные цифры числа π. Ваша цель — съесть как можно больше цифр числа π!
Примечание: данный код не будет корректно работать в Google Colab, поэтому мне пришлось встроить в него свой проект repl.it. Просмотреть исходный код можно здесь. Исходный код для данного проекта был взят у @LorenzoCampos, для пи-версии я внёс в него соответствующие изменения. Попробуйте сыграть!
8. Бинарное растровое изображение числа π
Число π также можно представить в двоичном виде. Я взял первый миллион шестнадцатеричных цифр числа π и побайтово конвертировал их в двоичный формат. Для вывода изображения на экран я представил первый миллион шестнадцатеричных цифр в виде монохромного чёрно-белого изображения с разрешением 2000×2000. Нули выводятся в виде чёрных пикселов, единицы – в виде белых.
После запуска кода изображение в окне вывода какое-то время будет белым. Нужно немного подождать, так как загрузка изображения в Colab обычно занимает некоторое время. Изображение также записывается в папку «output». Его можно загрузить на вкладке file (файл) в левой части блокнота Colab. Для формирования изображения в скрипте используется модуль Pillow.
9. Сочинение музыки с помощью числа π
С помощью числа π можно даже сочинять музыку. В приведённом ниже скрипте используется модуль numpy, рассчитывающий волновые формы, и модуль scipy, записывающий результат в файл a.wav. Чтобы не загромождать блокнот большим объёмом кода, часть кода реализована как вызов скрипта piaudio.py. Данный скрипт сопоставляет string note с конкретными частотами и формирует выбранную волновую форму для каждой ноты на основе её длительности и BPM.
Поэкспериментируйте со словарём нот, и, возможно, вам удастся с помощью числа π сгенерировать интересные мелодии. Присвойте кнопкам на клавиатуре определённые цифровые значения. Комментарии следует заводить только в указанном ниже формате. Кроме того, подставив в функцию play_note() аргумент waveform, можно задавать тип волновой формы. Таким типом может быть синусоида, треугольник, пила или квадрат.
В 20-й или 22-й строке указывается, какие цифры числа π будут использоваться — десятичные или шестнадцатеричные. По умолчанию в скрипте используются только первые 100 цифр числа π. Чем больше цифр, тем больше времени занимает расчёт.
В окне вывода появится окно воспроизведения, в котором можно прослушать и оценить полученную музыку. Файл можно сохранить в формате .wav. Аудиофайл также записывается в папку «output». Его можно загрузить через файловое меню (в левой части блокнота).
Пояснения по формату записи нот:
-
Обозначения нот должны начинаться с NOTE_.
-
Первая буква означает ноту: от A до G.
-
Первая буква «S» означает диезы (не бемоли).
-
Число означает октаву на клавиатуре, 0 — самая низкая, 8 — самая высокая.
10. Создание арт-объектов с помощью числа π в среде Processing

Processing — это среда, в которой реализован простой и быстрый инструментарий для программирования изображений, анимаций и интерфейсов. Библиотека графических объектов и интегрированная среда разработки (IDE) предоставляются пользователям бесплатно. Объекты программируются на Java, но при желании можно включить режим Python mode.
Просто так запустить код Processing в Google Colaboratory не получится. Вначале нужно загрузить Processing и установить дополнение Python Mode. Следуйте инструкциям Руководства по началу работы.
Данный скрипт Processing анализирует первые 10 000 десятичных цифр числа π и выводит их на экран в виде цветных кругов. Цвет круга соответствует цифре.
Получившийся рисунок можно загрузить здесь. Для создания изображения представлен код. Здесь можно также просмотреть/загрузить скрипт из моего репозитория GitHub.
11. Использование числа π для поиска связи с Кевином Бейконом
Данный скрипт демонстрирует способ использования цифр числа π как генератора псевдослучайных чисел в алгоритме.
Попробуем сыграть в игру Шесть шагов до Кевина Бейкона с помощью числа π. «Шесть шагов до Кевина Бейкона» — это игра / мысленный эксперимент, разновидность теории «шести рукопожатий». Теория «шести рукопожатий» — социологическая теория, согласно которой любые два человека на Земле разделены не более чем пятью уровнями общих знакомых (и соответственно шестью уровнями связей). Так как мы здесь развлекаемся, выберем предельно несерьёзный способ исследования этой теории — загрузим случайную страницу Википедии и будем переходить по ссылкам на этой странице на другие страницы, пока не попадём на страницу Википедии со статьёй о Кевине Бэйконе.
На исходной странице скрипт получит перечень всех статей Википедии, на которые присутствуют ссылки на данной странице. Затем скрипт, последовательно применяя цифры шестнадцатеричной записи числа π, определяет, на какую следующую страницу Википедии будет осуществлён переход.
Выполнение приведённого ниже скрипта может занять довольно много времени, но в итоге мы рано или поздно попадём на статью про Кевина Бейкона. Мой рекорд минимального количества страниц на пути к статье про Кевина Бейкона — 2 254.
Помимо создания подобных развлекающих вещей, Python предоставляет программисту широчайшие возможности. Этот язык давно стал основным для сферы data science, data analytics и веб-разработки, которая рассматривается на курсе Fullstack-разработчик на Python. Хотите добавить себе новый скил, который сделает вас ещё более крутым специалистом — приходите!

Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ
ссылка на оригинал статьи https://habr.com/ru/company/skillfactory/blog/548948/
Добавить комментарий