Примитивы Desbordante: Функциональные зависимости и их применение в эксплорации и очистке данных

Функциональные зависимости – концепция, которой уже много десятков лет, её преподают практически в каждом курсе баз данных. Их классическое применение – нормализация схемы данных. В последние годы у концепции появилось множество иных приложений в контексте data science, касающиеся эксплорации и очистки данных.

В статье мы расскажем о функциональных зависимостях (точных и приближенных), опишем, что с ними можно делать в контексте работы с данными, и покажем, что с ними умеет делать наш профайлер Desbordante. Статья является продолжением нашей прошлой статьи, в которой мы рассказали о профилировании данных.

Функциональные зависимости и приближенные функциональные зависимости

Неформально функциональная зависимость $A \rightarrow B$ (A и B — некоторые колонки в таблице) это правило, которое говорит, что для каждой пары строк верно, что из совпадения значений по А следует совпадение значений по В.

Рассмотрим пример. Можно сказать что в таблице слева присутствует функциональная зависимость $A \rightarrow B$ , так как нулю всегда соответствует единица, а единице – двойка. При этом, в таблице справа зависимости $A \rightarrow C$ нет, так как нулю одновременно может соответствовать и единица, и тройка. Вообще-то, концепция зависимости не привязана к конкретной таблице, а, скорее к области, моделируемой таблицей. Это значит, что в первой таблице зависимость может и не выполняться, например, потому что строка, “ломающая” ее, еще не была добавлена, но в принципе она возможна. Однако, в данной работе мы будем говорить, что зависимость есть, если в конкретной таблице данные ей не противоречат.

Выше мы опустили некоторые детали для понятности. Формально, зависимость определяется следующим образом:

Отношение удовлетворяет функциональной зависимости $X \rightarrow Y$ (где $X, Y \subset R$ тогда и только тогда, когда для любых кортежей $t_1, \ t_2 \in R$ выполняется: если то

То есть, и левая, и правая часть может состоять из нескольких атрибутов. При этом, для функциональных зависимостей есть проработанная теория и свойства [1]. Например, согласно аксиомам Армстронга, каждая зависимость со сложной правой частью может быть разложена на несколько, то есть $A \rightarrow BC$ влечет за собой $A \rightarrow B$ и $A \rightarrow C$ . Кроме того, по тем же аксиомам Армстронга, из зависимости $AB \rightarrow BC$ можно исключить из обоих частей, и получить зависимость $A \rightarrow C$ .

Используя эти преобразования, можно выделить наиболее интересный класс зависимостей, так называемые минимальные и нетривиальные. Это значит, что для некоторой зависимости $X \rightarrow Y$ выполняется:

нетривиальность, то есть правая часть зависимости не является подмножеством левой ( $Y \nsubseteq X$ ).
минимальными, то есть нет такой зависимости $Z \rightarrow X$ , что $Z \subset X$ .

Первое правило говорит о том, что нет такого атрибута, который бы содержался в левой и правой части. Добавив любой атрибут одновременно в левую и правую часть, мы сделаем любую зависимость выполняющейся. Второе правило говорит о том, что нет такой зависимости, в которую бы “вкладывалась” эта. Дело в том, что по этим правилам получается, что в левую часть выполняющейся зависимости можно добавлять любой атрибут, и зависимость не “сломается”.

Кроме того, для практических целей наиболее удобны зависимости, в которых правая часть состоит из одного атрибута.

Точные функциональные зависимости имеют весьма существенные ограничения в применимости. Дело в том, что они очень строги, и поэтому очень малая доля сущностей реального мира может быть ими описана. Поэтому было придумано определение приближенной функциональной зависимости (Approximate Functional Dependency, AFD), которая описывается следующим образом.

Для некоторой приближенной функциональной зависимости $X \rightarrow Y$ и таблицы ее ошибка вычисляется следующим образом:

$e(X \rightarrow Y, r) = \frac{|\{(t_1, t_2) \in r^2 | t_1[X] = t_2[X] \wedge t_1[Y] \neq t_2[Y]\}|}{|r|^2 - |r|}$

AFD $X \rightarrow Y$ удерживается на если $e(X \rightarrow Y,\ r)\ \leq\ e_{max}$ .

Здесь идея следующая. Подсчитывается доля всех попарных несовпадений по правой части ко всему множеству пар и, если она меньше установленного пользователем порогового значения threshold, то считается, что зависимость есть. Согласно этой формулировке параметр threshold, это не процент записей, где нарушается зависимость, хотя он и лежит в диапазоне [0;1]. На самом деле, это просто некоторое число, и чем оно ближе к нулю, тем меньшее количество нарушений выявляется в данных. Тем самым, рассматриваемая зависимость ближе к точной.

В некоторых работах атрибуты, между которыми может существовать зависимость, рассматриваются как случайные величины, которые статистически зависимы друг от друга. В случае подобного обобщения зависимостей подразумевают, что некоторое значение определяет но не «наверняка», а с достаточно высокой вероятностью, а между самими величинами наблюдается корреляция.

Этот взгляд основан на предположении, что исследуемые данные могут быть описаны некоторой функцией плотности распределения вероятностей, а сама функциональная зависимость определяется как условная вероятность наступления события «совпадения» значений:

$Pr(I_{ij}[Y]=1|t_{i}[X]=t_{j}[X]) = 1 - \epsilon$

где:

— $I_{ij}[Y]$ это индикаторная функция, принимающая если для двух кортежей и справедливо

— $\epsilon$ – некоторая константа, по своей природе аналогичная ошибке, которую мы определяли для приближенных зависимостей.

Однако, методы поиска зависимостей в такой постановке задачи отличаются от тех, что используются для классических приближенных зависимостей. Здесь, вместо исследования пространства возможных сочетаний атрибутов и пересечения партиций (поговорим про это дальше), зависимости выводятся на основе факторизации обратной матрицы ковариации между элементами случайного вектора (который и представляет исследуемые данные).

Это альтернативный взгляд на функциональные зависимости, который мы не будем разбирать в рамках этой, вводной статьи. Интересующийся читатель может ознакомиться с этими идеями по ссылке [2].

Поиск функциональных зависимостей

Имея набор данных, можно найти все функциональные зависимости, в нем содержащиеся (как точные, так и приближенные). Для этой цели существует множество алгоритмов, которые можно разделить на три группы:

Алгоритмы, использующие обход алгебраических решеток (Lattice traversal algorithms)
Алгоритмы, основанные на поиске согласованных значений (Diﬀerence- and agree-set algorithms)
Алгоритмы, основанные на попарных сравнениях (Dependency induction algorithms)

Идея алгоритмов первой группы заключается в представлении пространства поиска функциональных зависимостей в виде алгебраической решетки, построенной на всех возможных комбинациях атрибутов. Алгоритм обходит эту решетку и проверяет каждую зависимость при помощи специальной структуры данных — партиции (представление столбца). При этом, алгоритмы данного типа способны сразу отсекать целые регионы решетки. К алгоритмам, обходящим алгебраические решетки относятся TANE, FUN, DFD, FD_MINE.

Алгоритмы второй группы используют концепцию difference- и agree-sets. Diﬀerence-set представляет собой множество кортежей, которые не совпадают по значениям, а agree-set наоборот — кортежи, совпадающие по значениям, причем для функциональных зависимостей рассматривается левая часть. Как и предыдущие, алгоритмы этой группы также используют партиции. Алгоритмы DEP_MINER и FastFDs являются примерами этой группы.

Наконец, алгоритмы последней группы применяют так называемую процедуру специализации, когда к не удерживающейся зависимости добавляются атрибуты до тех пор, пока она не станет выполняться. Здесь партиции не используются, а производится просто попарное сравнение кортежей для проверки зависимости. В качестве примера индукционного алгоритма можно назвать FDEP.

Более современные алгоритмы, такие как Pyro [3] и HyFD [4], обычно комбинируют несколько приемов из рассмотренных групп.

Как эти алгоритмы влияют на пользователя? Поиск зависимостей очень дорогое удовольствие, ведь количество возможных зависимостей, даже минимальных и нетривиальных, растет экспоненциально от количества колонок. Некоторые из алгоритмов лучше справляются с датасетами, где много атрибутов (“широкие”), другие специально ориентированы на датасеты с большим количеством строк (“длинные”). Наконец, и специфика самих данных (наполнение конкретной таблицы) может сказаться на производительности какого-то конкретного алгоритма.

Практически все из вышеупомянутых алгоритмов реализованы в Desbordante, и их можно применять.

Применение функциональных зависимостей

Что могут дать пользователю обнаруженные функциональные зависимости? В предыдущей работе мы обрисовали спектр пользователей, кому они могут быть интересны: ученые, всевозможные аналитики, специалисты по машинному обучению. Сейчас мы поговорим про аналитиков, и обсудим ту пользу, которую они могут извлечь из данных с помощью функциональных зависимостей (точных и приближенных).

1) Выявление ключей.

Если есть точная зависимость от некоторого атрибута (или группы атрибутов) ко всем остальным, то это указывает, что тот атрибут можно использовать в качестве первичного ключа.

2) Выявление опечаток и других ошибок в данных.

Приведем небольшой пример. В таблице ниже описаны предлагаемые некоторой компанией товары, пять разных вещей. Для каждой приведен ее заводской серийный номер и цена продажи.

В таблице видно, что первая, третья и четвертая запись касаются одного и того же товара. Однако в четвертой записи вероятно закралась ошибка – возможно, оператор вводивший данные, не допечатал девятку. При таком способе представления данных интуитивно понятно, что должна выполняться функциональная зависимость $Serial \longrightarrow Price$ причем в идеале точная. Если же в Price есть ошибки, то будет выполняться ее приближенная версия с достаточно маленьким threshold.

Поэтому можно поискать приближенную зависимость и поглядеть на строки, где она нарушается. Выполнив сравнение с другими строками с той же левой частью, можно было бы обнаружить правильный вариант ответа. На этой идее основан наш пайплайн по поиску ошибок в данных, о котором будет ниже.

3) Заполнение пропущенных значений.

Обратимся опять к предыдущему примеру, однако будем считать, что на той строке просто ничего не написано. Аналогичным образом можно воспользоваться существующей зависимостью и применить эту же процедуру. Конечно, может случиться так, что это единственная строка с такой же левой частью. В таком случае восстановить данные не получится. Однако типов зависимостей очень много, и есть и такие, которые могли бы сработать и в данном случае, дав хотя бы подсказку.

Далее, а как узнать, есть ли зависимость между некоторой парой колонок? Или даже так: допустим есть столбец, который надо проверить (правая часть), надо найти подходящий атрибут левой части. Это можно сделать, посмотрев на матрицу корреляций, и выбрать для данной колонки наиболее подходящие.

При этом сами по себе коэффициенты корреляции не пригодны для решения этих задач, так как они не дадут указания на конкретные строки, в которых что-то есть. Их можно получить только с помощью зависимостей.

Больше про применение зависимостей (причем не только функциональных, но и других типов) можно почитать тут [5, 6].

Что может делать Desbordante?

Для работы с зависимостями в Desbordante на данный момент есть следующая функциональность:

1) Поиск функциональных зависимостей, включая приближенные.

2) Поиск ошибок в данных (опечаток).

Поиск зависимостей

Рассмотрим сначала поиск зависимостей. Desbordante реализован так, чтобы искать минимальные нетривиальные функциональные зависимости с правой частью, состоящей из одного элемента (о них говорилось выше). Все остальные могут быть получены из выдаваемого набора путем применения преобразований из аксиом Армстронга.

На скриншоте вверху показан выбор этого примитива. Пользователь может указать датасет или выбрать из встроенных, причем работает drag-n-drop. Как уже отмечалось в прошлой статье, для загрузки своих датасетов необходима регистрация. Далее следует выбрать разделитель и указать, есть ли в файле строка-заголовок.

Искать зависимости можно несколькими алгоритмами, перечисленными выше. Каждый алгоритм имеет свои особенности, и подходит для своего типа датасета (например, для “широкого” или же “длинного”). Поэтому, если датасет не проходит по таймлимиту или “падает” от нехватки памяти, имеет смысл попытаться поменять алгоритм. Наилучшей дефолтной опцией в настоящий момент будет Pyro. Он является одним из наиболее производительных, достаточно универсален и имеет многопоточную реализацию.

Некоторые из алгоритмов могут работать с приближенными зависимостями. Для этого доступен параметр error threshold. Если же он выставлен в ноль, это значит, что будут искаться точные функциональные зависимости.

Теперь поговорим про арность (Arity constraint). Выше мы писали про то, что ищем минимальные зависимости, то есть такие, в которых нет “лишних” атрибутов, что значительно сокращает выдачу. Однако этого довольно часто бывает недостаточно, и надо сокращать выдачу далее.

Дело в том, что чем шире таблица, тем больше возможных зависимостей рассматриваемого типа может быть найдено, ведь их количество растет как от числа атрибутов в таблице. При этом, найденные зависимости имеют различную ценность для пользователя, причем напрямую зависящую от длины левой части. Зависимости с более короткой левой частью являются более ценными, нежели с длинной. Действительно, для того чтобы “сломать” зависимость с ростом левой части, нужно экспоненциально больше данных. То есть, в реальных сценариях применения, найденная зависимость с “длинной” левой частью обычно говорит о том, что просто не нашлось данных, в которой была бы строка контрпример. Поэтому довольно часто имеет смысл ограничивать длину левой части, чтобы, во-первых, не рассматривать нерелевантные зависимости, а во-вторых, сэкономить время выполнения. Поиск зависимостей очень дорогой процесс, и, прервав его на нижних уровнях решетки, можно получить значительный выигрыш во времени.

В Desbordante ограничение арности позволяет указать алгоритму, что требуются зависимости с длиной левой части не более чем .

Теперь о выдаче. Она представляется тремя экранами:

Атрибуты
Зависимости
Данные

На рисунке ниже представлен экран атрибутов. На нем есть две круговые диаграммы – одна для левой части, другая для правой. Каждая из них показывает частоту появления атрибута в общем наборе найденных зависимостей. Зависимости можно фильтровать, путем ввода или клика на атрибуты. При этом, считается, что набранные атрибуты объединены с помощью предиката “или”, то есть в выдаче будут все зависимости в которых есть хотя бы один из выбранных атрибутов. Диаграмма интерактивна, выбрав атрибут, доля оставшихся пересчитывается.

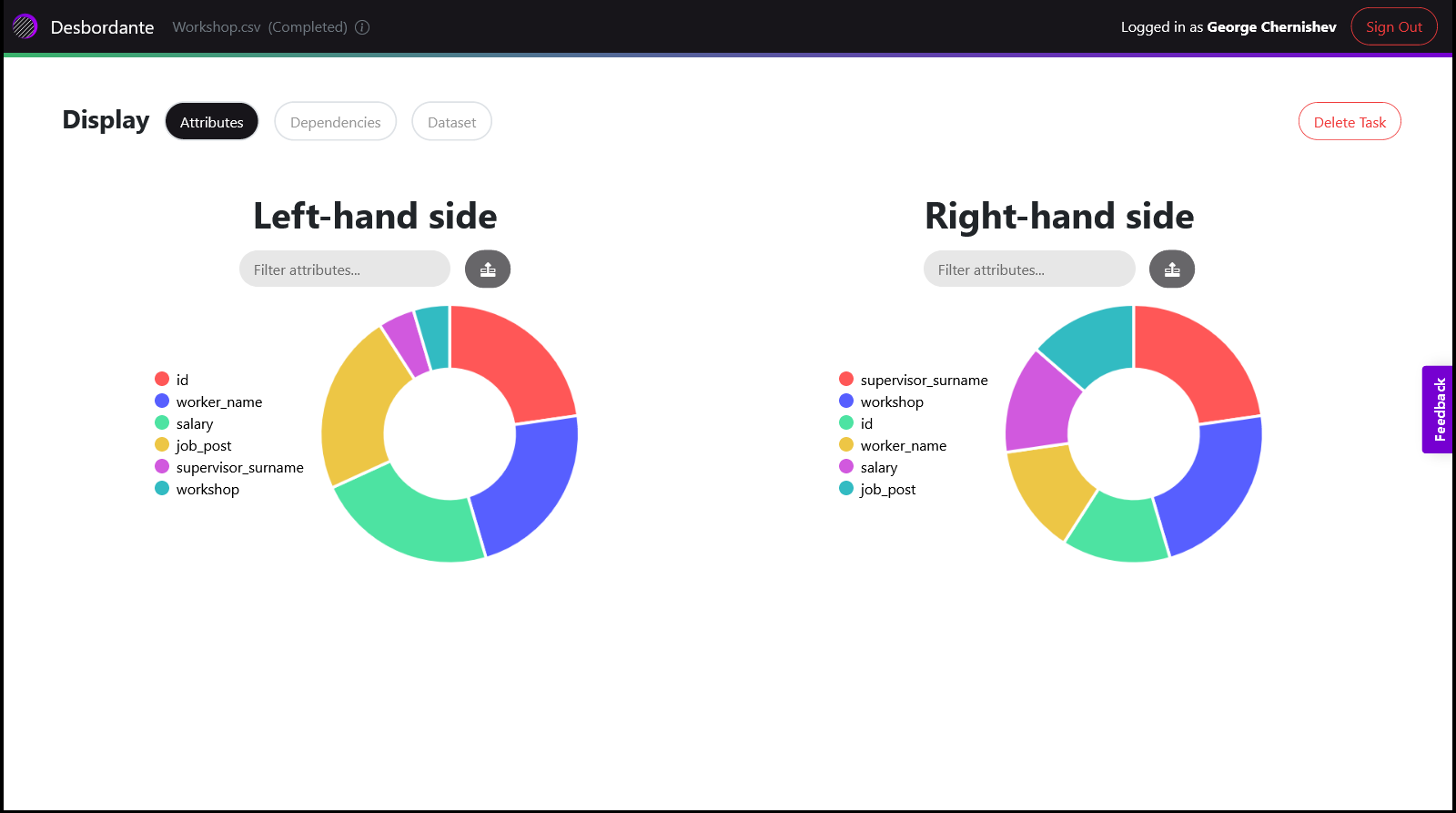
При нажатии на кнопку Dependencies можно перейти к списку найденных зависимостей в соответствии с выбранным фильтром. Сам список зависимостей позволяет проводить их сортировку, по левой и по правой части, а также делать фильтрацию. Кроме того, есть возможность показать найденные ключи – атрибуты, которые функционально определяют все остальные.

На экране датасета можно будет увидеть сам датасет (вернее его сниппет), и если на экране зависимостей была выбрана какая-то зависимость, то она будет выделена в данных. Сам сниппет небольшой, представляет собой первые сто строк таблицы.

Поиск ошибок

Теперь к “ноу-хау” Desbordante, а именно, возможности использовать базовые примитивы, такие как функциональные зависимости, в целях решения каких-то продуктовых задач. Для этого используются композиции примитивов, которые мы называем пайплайнами. В настоящий момент Desbordante предлагает один такой пайплайн, называемый Error Detection Pipeline. С помощью него можно искать ошибки в данных, такие, как, например, опечатки. Его идея состоит в том, что ошибок обычно меньше, чем правильных данных, и это будет видно по удерживающимся приближенным функциональным зависимостям.

В двух словах подход можно описать следующим образом. Путем запуска поиска точных и приближенных зависимостей находятся такие зависимости, которые “почти” выполняются на данных. То есть, некоторый набор строк не удовлетворяет точной функциональной зависимости, но удовлетворяет приближенной. “Степень” такой ошибки задается пользователем путем указания параметра threshold у алгоритма поиска приближенных функциональных зависимостей. Как она вычисляется было рассказано выше, когда мы вводили приближенные функциональные зависимости.

С каждой из этих зависимостей пользователь может поработать отдельно. Desbordante может показать все строки таблицы, где нарушается зависимость, то есть все записи с одинаковыми левыми частями, но разными правыми. Однако, как показала практика, будет выдано слишком много информации и в ней будет трудно разобраться. Говоря более конкретно, наборов с одинаковыми левыми частями (мы их называем кластерами) может быть слишком много, если выбранный threshold (или сами данные) не слишком удачен.

Поэтому пользователю дано два дополнительных параметра – radius и ratio.

Идея заключается в следующем: кластер отображается, если доля* его записей, лежащих внутри некоторого radius, меньше, чем ratio. Radius — значение, которое показывает, насколько близки должны быть строки к «центру» кластера, чтобы считать их опечатками. Центром кластера мы будем называть самую распространенную в нем запись. И получается, что radius, это некоторый радиус локальной окрестности, отсчитываемый от этой записи. Radius может принимать значения в диапазоне $[0, +\infty)$ .

В свою очередь, параметр ratio задает максимальную долю отличающихся от центра, но близких к нему значений, чтобы весь кластер целиком считался содержащим опечатки (и, соответственно, выводился). Она лежит в диапазоне .

Что значит “лежащих внутри некоторого radius”, какие это записи? Это все записи, у которых расстояние от них до записи, которая наиболее часто встречается в данном кластере, меньше, чем radius. Расстояние между записями мы будем считать по правой части указанной функциональной зависимости, так как именно они и отличаются в рассматриваемом случае.

* Доля — это отношение количества записей, которые не равны самой распространенной в кластере, к общему количеству записей в кластере.

Как вычислять расстояние между правыми частями? Для этого может быть использована некоторая метрика. В настоящий момент Desbordante поддерживает следующие метрики:

Разница для целочисленных или вещественных значений.
Расстояние Левенштейна для строк.

При этом, надо понимать, что для каждой зависимости метрика может быть своя, в зависимости от типа правой части функциональной зависимости. Desbordante будет выбирать ее автоматически.

Рассмотрим визуализацию этой идеи. Пусть у нас есть зависимость $“цех” \longrightarrow “начальник\,цеха”$ Так как правая часть будет иметь тип строки, то будет использоваться расстояние Левенштейна. Допустим, пользователь выставил radius в 1, а ratio в 0.2. Это значит, что в окрестность будут попадать записи с правой частью, отличающиеся не более, чем на единицу (на один символ), и такие записи должны составлять не более 20% от всех в кластере. Предположим, что у нас есть два кластера, изображенные ниже.

На рисунке каждая * обозначает точку, которая подписана зависимостью и количеством записей (через x). В обоих случаях центром кластера будет запись (5, masha), а подписи на стрелках показывают расстояние до центра. Согласно вышеописанным правилам кластер слева будет показываться при заданных параметрах, а тот что справа — нет. Исходя из того, что слева строчки “слабо” отличающиеся от центра встречаются “редко” можно сделать вывод, что слева вероятно есть ошибка, а вот в случае справа ее скорее всего нет. Характеристики “слабо” и “редко” как раз и задаются через параметры radius и ratio соответственно. Предлагаемый механизм позволяет пользователю выделить интересные случаи и поработать с ними.

Вообще, пользователь может хотеть искать ошибки двух типов:

Локальные ошибки, опечатка в одной букве или небольшая ошибка в числе, потому что измерительный прибор сбоит и, например, дает 4.00, 3.99, 4.00000001.
Глобальные выбросы, которых должно быть мало, один-два-три на кластер, например последовательность “mikhail”, “mikhail”, “mikhail ivanovich”.

Подход с двумя параметрами radius и ratio дает возможность пользователю Desbordante обработать оба этих случая.

Из всего вышесказанного получается следующий сценарий использования. Допустим, у нас есть в таблице атрибуты “цех” и “начальник цеха”, оба текстовых. Мы выставили threshold приближенной зависимости в 0.1 и нашли зависимость $“цех” \longrightarrow “начальник\,цеха”$

Фиксируем расстояние radius, ставим его в единицу. У нас в данном случае расстояние Левенштейна, поэтому будем искать опечатки в одну букву.
Ставим ratio в 20%, и получаем проверку локальных ошибок. Система выдаст кластер с локальными ошибками, например такой:

(x47) 15 -> Masha

(x1) 15 -> Msha

(x1) 15 -> Misha

В скобках отображено количество записей, система “выбрала” запись “Masha” как центр кластера (как самое распространенное в кластере).

Пользователь исправляет* обе локальные ошибки и перезапускает пайплайн.
Потом он выставляет radius в 20 и уже видит дальние выбросы, в других (или тех же) кластерах:

(x32) 12 -> Misha

(x1) 12 -> Mihail Ivanovich

(x1) 12 -> Masha

Обрабатываем их, исправляя или удаляя.
Можно увеличивать radius и находить еще более дальние выбросы, пока пользователь не сочтет, что далее не стоит работать с этими данными.
Если есть предположение, что данные очень грязные, то можно попробовать поувеличивать ratio, однако тут важно не переусердствовать, и не выставлять слишком большое значение. Интуитивно можно сказать, что ratio > 50% смысла не имеет (а 50% имеет только для кластеров из двух значений). А, скажем, ratio в 90% ratio обозначает, что в кластере 90% значений — опечатки, чего явно быть не может. В любом случае кажется, что пользователь должен попробовать несколько значений ratio и radius.

* Причем может и не исправлять, а просто удалить эти записи, чтобы убрать их из выдачи. Это может может быть полезно когда качество этих данных устраивает, но они портят зависимость.

В дальнейшем мы планируем расширить возможности по фильтрации кластеров, добавив новых условий и ограничений, или же поиск кластеров по другим критериям, без привязки к некоторой “центральной” записи. А также автоматический подбор “хороших” параметров.

Теперь рассмотрим, как это всё выглядит на практике, начав с простого примера. Мы выбираем встроенный датасет SimpleTypos с указанными параметрами. В нем есть три колонки OneTypo, TwoTypos и A.

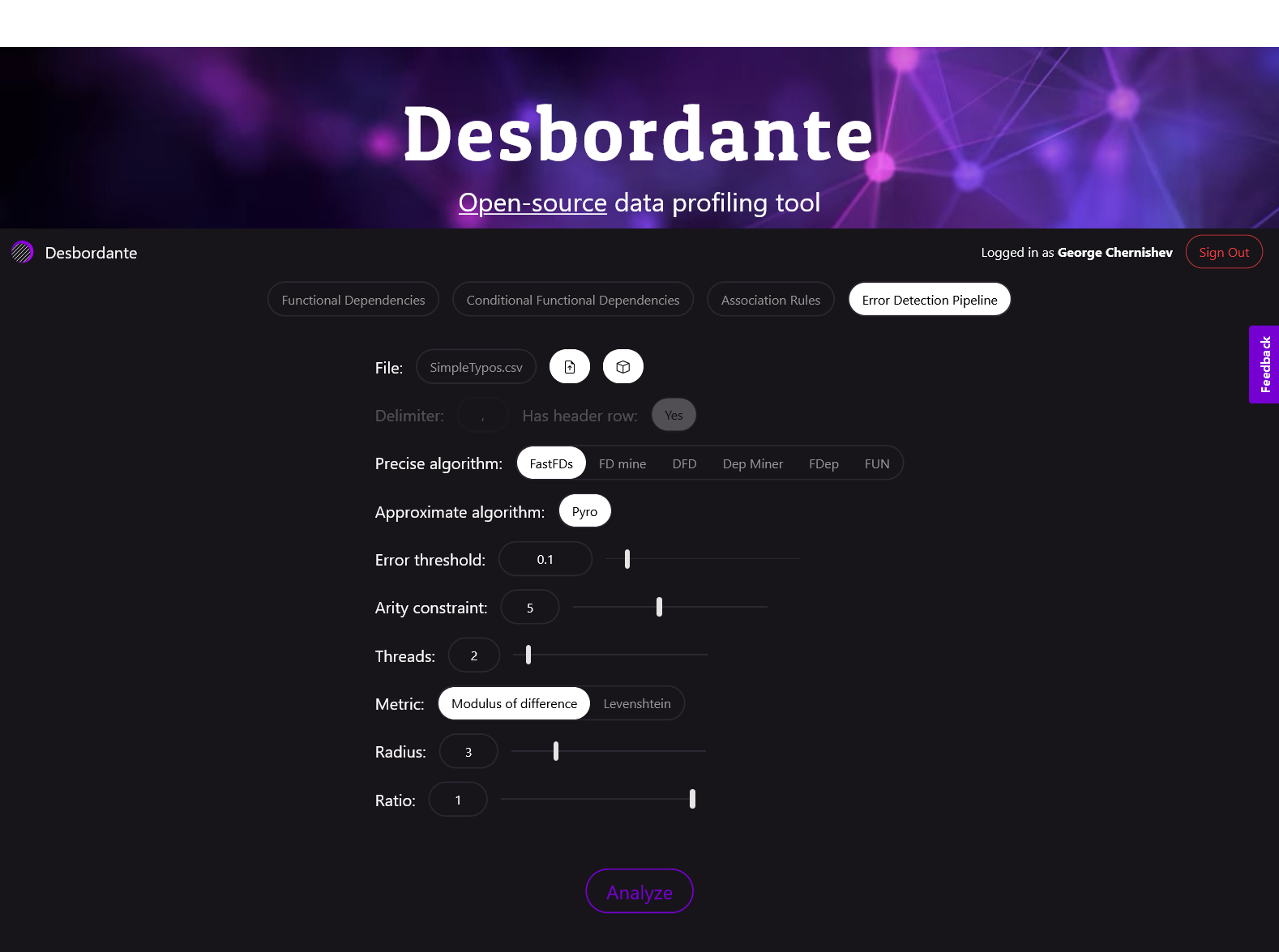
Для удобства демонстрации параметры уже заранее подготовлены и привязаны к датасету, поэтому можно сразу нажать кнопку Analyze. Этот датасет у нас численный, поэтому в качестве расстояния используется модуль разности. Взглянем на сам датасет:

Запустим пайплайн с дефолтными параметрами. Вот что он выдаст:

Здесь видно, что есть две зависимости, которые почти удерживаются. Выберем первую из них ( $OneTypo \longrightarrow TwoTypos$ ) и перейдем ко вкладке clusters, там будут показаны все кластера, где зависимость не удерживается, и где, вероятно, есть ошибки.

Тут мы видим две строки нашей таблицы, в которых есть нарушение. Строки с номером 7 и 9 имеют совпадение по левой части (OneTypo), но различаются по правой части (TwoTypos). Причем они довольно близки, укладываются в radius, равный единице. Это может означать, что какая-то из этих двух строк неверна.

Теперь давайте поглядим на исходный датасет еще раз и убедимся что там действительно присутствует ошибка:

Из таблицы видно, что только тройке соответствуют различные значения, поэтому и выдается только этот, единственный кластер. Кроме того, видно, что рассматриваемая функциональная зависимость почти удерживается на данных, а выставленного threshold (0.1) хватает, чтобы найти ее приближенную версию.

Чтобы дать возможность понять работу инструмента мы сделали так, чтобы заинтересовавшийся пользователь смог найти еще три ошибки. Поигравшись с параметрами, можно найти еще ситуации, когда зависимости $A \longrightarrow OneTypo$ и $A \longrightarrow TwoTypos$ покажут наличие других ошибок – одной и двух в соответствующих столбцах.

Теперь рассмотрим другой, более серьезный, пример, представленный датасетом workshop. Мы также запускаем пайплайн на выполнение с дефолтным параметрами. Сам датасет представляет собой какую-то базу данных работников, есть колонки работник, позиция, зарплата, начальник цеха и сам цех, где они трудятся. Сами данные выглядят как-то так:

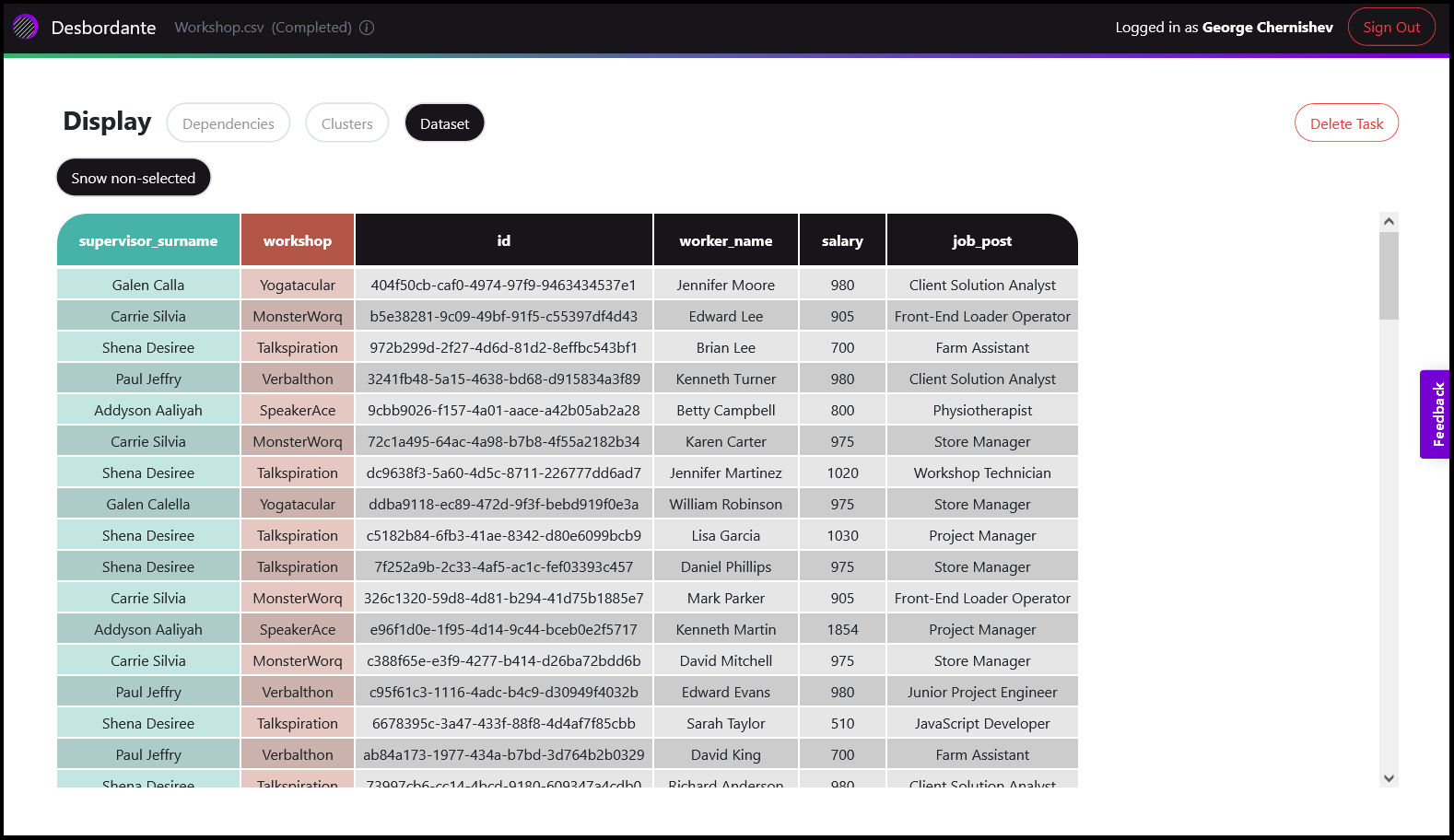
Теперь откроем вкладку Dependencies и поглядим, что там есть. Здесь уже гораздо больше всяких зависимостей, но давайте остановимся на $workshop \longrightarrow supervisor\_name$

Выбрав ее, переходим на вкладку clusters, и смотрим на выдачу.

Эта таблица уже большая, там где-то тысяча строк. И вот мы видим один кластер, тоже большой, от него показываются только первые десять строк. Дело в том, что на этом экране может быть показано несколько кластеров (если найдется), поэтому имеет смысл экономить место. Полностью кластер можно будет подгрузить кнопкой “Load More”, так что пользователь ничего не теряет.

Уже на этой выдаче видно, что есть опечатка в фамилии начальника цеха. Причем кажется, что проблема в записи номер семь, так как она одна. Но чтобы убедиться в этом, надо взглянуть на все данные этого кластера. Начав делать это с помощью Load More мы столкнемся с морем записей, которые тяжело обозреть взглядом. Для помощи в этом случае есть две кнопки: sorted и squashed. Первая – просто сортирует записи по уникальности значения в правой части (таким образом самые редкие значения будут вверху таблицы); вторая “сжимает” существующие, выводя количество их появлений. Выглядит это так:

Ну и тут уже всё очевидно, ошибка заключается именно в двух лишних добавленных буквах фамилии. При этом заметим, что данные в колонках, не входящих в функциональные зависимости, выбраны случайно из имеющихся записей.

Таким образом, работа с инструментом требует экспериментирования: необходимо подбирать параметры и работать с данными – модифицировать и удалять строки. Данный пайплайн экспериментальный, планируем в дальнейшем его улучшать и дорабатывать. Будем рады любому фидбеку.

Заключение

В дальнейших статьях мы разберем другие примитивы этого класса, с более интересными формулировками, такими как условные функциональные зависимости (conditional functional dependencies) и метрические функциональные зависимости (metric functional dependencies). Первые уже можно попробовать на нашем сайте, а вторые пока есть только в консольной версии, но скоро появятся и на фронтенде.

Саму систему можно попробовать тут: https://desbordante.unidata-platform.ru/, гайды к ней есть на https://mstrutov.github.io/Desbordante/, а код выложен на https://github.com/Mstrutov/Desbordante/.

Ссылки

[1] Thorsten Papenbrock, Jens Ehrlich, Jannik Marten, Tommy Neubert, Jan-Peer Rudolph, Martin Schönberg, Jakob Zwiener, and Felix Naumann. 2015. Functional dependency discovery: an experimental evaluation of seven algorithms. Proc. VLDB Endow. 8, 10 (June 2015), 1082–1093. https://doi.org/10.14778/2794367.2794377

[2] Yunjia Zhang, Zhihan Guo, and Theodoros Rekatsinas. 2020. A Statistical Perspective on Discovering Functional Dependencies in Noisy Data. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data (SIGMOD ’20). Association for Computing Machinery, New York, NY, USA, 861–876. https://doi.org/10.1145/3318464.3389749

[3] Sebastian Kruse and Felix Naumann. 2018. Efficient discovery of approximate dependencies. Proc. VLDB Endow. 11, 7 (March 2018), 759–772. https://doi.org/10.14778/3192965.3192968

[4] Thorsten Papenbrock and Felix Naumann. 2016. A Hybrid Approach to Functional Dependency Discovery. In Proceedings of the 2016 International Conference on Management of Data (SIGMOD ’16). Association for Computing Machinery, New York, NY, USA, 821–833. https://doi.org/10.1145/2882903.2915203

[5] Data Profiling. Ziawasch Abedjan, Lukasz Golab, Felix Naumann, Thorsten Papenbrock. Synthesis Lectures on Data Management. Springer Cham. ISSN 2153-5418. ISBN 978-3-031-01865-7. https://doi.org/10.1007/978-3-031-01865-7

[6] Ihab F. Ilyas and Xu Chu. 2019. Data Cleaning. Association for Computing Machinery, New York, NY, USA.

Подготовили: Георгий Чернышев, Михаил Полынцов, Никита Бобров

ссылка на оригинал статьи https://habr.com/ru/company/unidata/blog/679390/