Метод K-ближайших соседей (KNN) — это тип контролируемого алгоритма ML.
К — ближайший сосед — это тот для которого наименьшее расстояние.
KNN использует “сходство признаков” для прогнозирования значений новых точек данных и присваивания значений, основанное насколько близко она соответствует точкам в обучающем наборе. Чтобы понять его работу определим шаги действий:
Шаг 1 − Загружаем обучающий и тестовый dataset.
Шаг 2 − Выбираем значение K, то есть ближайшие точки данных. Оно может быть любым целым числом.
Шаг 3 — Вычисляем расстояние между тестовыми данными и каждой строкой обучающих данных с помощью любого из методов. Наиболее часто используемый метод вычисления расстояния — евклидов.
Шаг 4− Отсортировываем в порядке возрастания, основываясь на значении расстояния.
Шаг 5 − Алгоритм выбирает верхние K строк из отсортированного массива.
Шаг 6 − Назначаем класс контрольной точке на основе наиболее частого класса этих строк.
Рассмотрим пример для понимания концепции K и работы алгоритма KNN
Задача классификатора определить связь между признаками переменной Х и целевой переменной у, которую предсказываем. Х —> у
В примере будем использовать готовый датасет с координатами точек 2-х классов (фиолетовый и желтый). Необходимо отделить точки.
Импорт библиотек
import matplotlib.pyplot as plt #отрисовка from sortedcontainers import SortedList #сортированный словарь from future.utils import iteritems #для цикла from sklearn.datasets import make_blobs #готовые данные from mlxtend.plotting import plot_decision_regions #отрисовкаСоздаем датасет
Создаем массив точек Х и у. Используем 30 экземпляров (строк). Два Х на каждый экземпляр.
X, y = make_blobs(n_samples=30, centers=2, n_features=2, random_state=0)Нарисуем Х и раскрасим в соответствии с классом у (0 или 1).
plt.scatter(X[:,0], X[:,1], s=100, c=y, alpha=0.5) plt.show()
Алгоритм KNN
Передаем к — количество ближайших соседей. Функция fit — запоминает координаты Х, которые соответствуют у и записывает в атрибуты. predict — двумерный вектор Х с координатами точек для которых неизвестен класс у. Меряем расстояние между нашей точкой и координатой из обучающей выборки. Определяем циклом расстояние между точками с помощью евклидово расстояние. Формула:
$\sqrt{(p1-q1)^2+(p2-q2)^2+(p_n-q_n)^2}$ Функция score — измерят точность алгоритма.
class KNN: def init(self, k): self.k = k def fit(self, X, y): self.X = X self.y = y def predict(self, X): y = np.zeros(len(X)) #Вектор Х для которого неизвестен у. enumerate - индекс элемента. for i, x in enumerate(X): sl = SortedList() for j, x_train in enumerate(self.X): diff = x - x_train d = diff.dot(diff) # Euclidian distance #другой вариант реализации Euclidian distance #np.linalg.norm(x - x_train) #К какому классу относятся точки if (len(sl) < self.k): sl.add( (d, self.y[j]) ) else: if (d < sl[-1][0] ): del sl[-1] sl.add( (d, self.y[j]) ) #Считаем у какого класса большее кол-во и назначаем его нашей точки votes = {} for _, v in sl: votes[v] = votes.get(v, 0) + 1 max_votes = 0 max_votes_class = -1 for v, count in iteritems(votes): if count > max_votes: max_votes = count max_votes_class = v y[i] = max_votes_class return y def score(self, X, y): P = self.predict(X) return np.mean(P == y)Тестируем модель
Пробуем с к = 1
model = KNN(k=1)Разделим данные на обучающие и тестирующие. Возьмем первые 20 для обучение и последние 10 для теста.
X_train, y_train = X[:20], y[:20] X_test, y_test = X[20:], y[20:]Обучаем модель
model.fit(X_train, y_train)Предсказываем наши значения и сравниваем получивший результат с тестовыми данными
y_pred = model.predict(X_test) y_pred == y_testОпределяем точность алгоритма
model.score(X_test, y_test)Отрисуем модель
plot_decision_regions(X, y, clf=model, legend=2) plt.xlabel('x1') plt.ylabel('x2') plt.show()
Протестируем с к = 10
model = KNN(k=10) model.fit(X, y) plot_decision_regions(X, y, clf=model, legend=2) plt.xlabel('x1') plt.ylabel('x2') plt.show()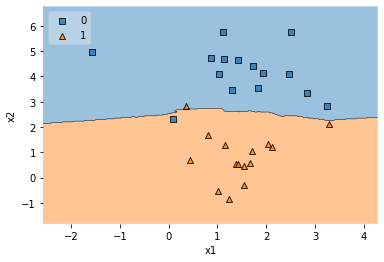
ссылка на оригинал статьи https://habr.com/ru/post/685014/
Добавить комментарий