Путешествие в космос или введение в симплекс-метод для школьников

0. Короткое введение

На Хабре уже были публикации о симплекс-методе раз и два. И они очень даже не плохи. Но проблема в том, что обычно симплекс-метод не изучают в школе, при этом школьники уже обладают достаточным багажом знаний для освоения этого метода. И попытка объяснить его школьникам была сделана в августовском номере журнала «Юный техник» за 1985 год. Я хочу привести эту статью здесь, а также добавить свои комментарии по поводу примера, разобранного в ней. Автор статьи: С.Волков. Рисунки Г.Заславской. Статья была размещена в рубрике «ЭВМ в твоих руках».

В процессе работы над настоящей статьёй для Хабра я написал письмо в редакцию журнала Юный техник с просьбой разрешить мне привести текст оригинальной статьи здесь полностью. И редактор дал мне такое разрешение! При том ответ пришёл очень быстро.

В настоящей статье я собираюсь сделать вот что:
1) Привести ссылку на скан оригинальной статьи (вот она: Путешествие в космос)
2) Привести текст самой статьи в перенабранном виде с тем, чтоб вам было удобней читать, а мне — ссылаться.
3) Чуть-чуть покритиковать эту статью, несмотря на то, что и сам журнал и статья эта мне очень нравятся! Разобрать, как можно было бы объяснить решение более понятно для школьников.
4) Всё-таки решить эту задачу с помощью ЭВМ.

Цель данной статьи на Хабре… ну, наверно, в том, чтоб, с одной стороны, вскрыть эдакую капсулу времени, а с другой, привлечь внимание учителей и школьников к этому методу. Всё-таки сама статья в ЮТ вышла уже больше 37 лет назад и вряд ли о ней часто вспоминают.

И ещё кое-что… Есть поговорка про то, что если дать человеку рыбу — то он будет сыт один день, а если научить его ловить рыбу — он будет сыт до конца жизни. Вот по-моему, симплекс-метод — это способ ловли рыбы. Грубо говоря, некоторые знания или навыки, которые можно получить даже будучи школьником — фактически могут составлять основу для целой профессии. Симплекс-метод — это как раз одно из таких умений. Этот метод используется очень много где, где нужно что-либо оптимизировать: например, для оптимизации маршрутов перевозки товаров; для оптимизации раскроя листовых материалов в производстве; в военном деле (для оптимизации логистики при перевозке боеприпасов и эвакуации раненых); в бизнесе для планирования затрат и доходов, принятия решения о том, кого нанять и кого уволить; в экономике и стратегическом планировании (кстати, очень многих войн попросту не случилось бы, если бы люди, которые их начинали — знали бы об этом методе). И при этом, освоить его может даже семиклассник. Необходимый для понимания минимум — умение решать системы линейных уравнений. Т.е. это даже не одна профессия, а целый букет. Звучит заманчиво? Тогда давайте же скорее начнём!

1. Ссылка на скан оригинальной статьи.

вот она: Путешествие в космос

2. Путешествие в космос (Юный техник, №8, 1985 год)

Ситуация, которую мы сегодня рассмотрим, фантастическая. Но задача, которую придётся решить, чтобы из этой ситуации выйти, вполне реальна.

Итак, представим, что наш космический корабль приближается к одной из планет соседней галактики. Взревели тормозные двигатели, и звездолет мягко касается посадочной площадки.

— Топливо — нуль,— объявляет бортовой компьютер.

Это значит, что бак звездолета пуст. Нужно заправиться. Выглядываем в иллюминатор и видим заправочную станцию.

На станции два вида топлива (естественно, оно необычно); топливо номер один называется «Антигравитон-10», другое «Антигравитон-7», сокращенно А-10 и А-7. Цифра в названии топлива показывает, сколько часов можно пролететь на одном его литре; топливный бак звездолета вмещает 5 л.

Какое же топливо выбрать? Очевидно, А-10 эффективнее, но 1 л его весит 3 кг, а общий вec топлива на борту нашего космолета не должен превышать 12 кг. Литр А-7 весит 2 кг. Можно залить им полный бак, он будет весить всего 10 кг, но запас хода окажется равным 35 часам.

Есть еще вариант: залить в бак сразу оба сорта топлива (они не перемешиваются) и использовать их поочередно. Но какого топлива сколько взять на борт?

Для решения подобных задач, довольно часто встречающихся в физике, пользуются так называемым симплекс-методом, применяемым в линейном программировании. Что это такое, мы покажем при решении нашей задачи, но сначала сформулируем ее условие.

Итак, 1 л антигравитона А-7 — это 7 часов полета. Значит, если мы возьмем на борт Х₁ литров, то летное время составит 7X₁ часов. Точно так же Х₂ литров А-10 гарантируют нам 10Х₂ летных часов, а всего летное время составит

$T = 7 X_1 + 10 X_2\hspace{3em}(1)$

часов.

Наша цель — сделать летное время Т как можно больше, но при этом нужно учесть, во-первых, что топливный бак вмещает всего 5 л. Значит, общий объем горючего не может превышать это значение, то есть

$X_1 + X_2 \le 5\hspace{5em}(2)$

Во-вторых, вес топлива не должен превышать 12 кг. Литр А-10 весит 3 кг, значит, общий вес топлива этого сорта будет ЗХ₂, а литр А-7, как сказано, весит 2 кг. Его вес равен 2Х₁, а всего горючее весит

$2 X_1 +3 X_2 \hspace{6em}(3)$

У нас получилась следующая задача:

максимизировать

$T = 7X_1 + 10 X_2\hspace{5em}(1)$

при ограничениях

ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ $X_1+X_2\le5$ ,ㅤㅤㅤㅤㅤㅤㅤ(5)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ $3X_1+2X_2 \le 12$

Для решения ее прежде всего надо заменить неравенства равенствами. Если мы зальем меньше 5 л топлива, то какой- то объем бака останется неиспользованным, обозначим его через Х₃. Тогда сумма объема топлива и пустой части бака даст нам как раз 5 л, то есть

$X_1+X_2+X_3 = 5\hspace{4em}(6)$

Точно так же поступим и с весовым ограничением. Неиспользованный вес назовем Х₄ и в конце концов перепишем нашу задачку так:

ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,ㅤㅤㅤㅤㅤ(7)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ

Любое решение этой системы даст нам объемы каждого сорта топлива, полетное время и величины неиспользованных объема и веса. Но переменных пять, а уравнений только три, значит, система имеет не одно решение. Мы должны найти такое, когда Т — летное время — будет максимальным. Предположим, что мы вообще не заправили космолет, то есть Х₁=Х₂=0. Тогда, естественно, летать просто невозможно, Т=0, а Х₃=5 и Х₄=12. Мы получили одно из решений нашей системы, конечно, не наилучшее. Это решение называют исходным опорным планом. Переменные, входящие в опорный план, называют базисными переменными или просто базисом. В нашем случае это Т, Х₃ и Х₄. Обратите внимание: каждая базисная переменная входит только в одно уравнение и коэффициент при ней равен 1. Так как же улучшить опорный план? Для начала начнем заправку космолета. Только не будем заливать оба сорта топлива сразу, возьмем только один.

С точки зрения математики это будет означать, что либо Х₁ —объем А-7, либо Х₂— объем А-10— станет отличным от нуля, то есть одна из этих переменных пойдет в базис. Какое же топливо залить, или, что то же самое, какую переменную ввести в базис? Наверное, Х₂.

А-10 эффективнее, и введение в базис Х₂ сильнее влияет на Т. Это видно и из нашей системы. В самом деле, коэффициент при Х₂ равен 10. Значит, увеличение Х₂на 1 уменьшает левую часть на 10. Чтобы равенство сохранилось, приходится увеличить Т тоже на 10. Тогда как увеличение на единицу Х₁ приводит к возрастанию Т только на 7. Вот мы и получили первое правило симплекс-метода: в базис вводится та переменная, которая имеет наибольший по абсолютной величине отрицательный коэффициент. А количество А-10, которое нужно залить, определяют ограничения. Ведь при заполнении бака уменьшаются пустой объем Х₃ и неиспользованный вес Х₄. Какая-то из этих величин в конце концов обратится r нуль—или бак окажется наполнен, или лимит веса будет исчерпан.

А это, кстати, означает, что переменная, которая стала равной 0, исключится из базиса. Какую же исключить — Х₃ или Х₄?

Из второго соотношения следует, что если Х₂ увеличить на 1, то Х₃ уменьшится на столько же. А начальное значение пустого объема было 5. Значит, максимальная величина Х₂ не может быть больше 5. Ведь нельзя залить топлива больше, чем вмещает бак.

В третьем соотношении увеличение Х₂ на единицу уменьшает Х₄ сразу на 3, ведь 1 л весит 3 кг. Именно на столько убывает неиспользованный вес при добавлении каждого литра топлива. А всего можно залить 12:3=4 л. В результате получаем, что Х₂ не превышает 4. Ну что ж, зальем 4 л А-10, при этом лимит веса будет исчерпан 2X₄=0. Эта переменная исключается из базиса, а вместо нее входит Х₂.

Вот мы и получили второе правило симплекс-метода: новая базисная переменная увеличивается до тех пор, пока какая-нибудь из переменных старого базиса не обратится в нуль. Теперь в новый базис входят Т, Х₃ и Х₂. Значит, надо соответственно преобразовать систему уравнений, чтобы Х₂ присутствовало только в одном уравнении, в третьем, с коэффициентом 1.

Для этого разделим последнее уравнение на 3, затем вычтем его из второго. Тогда переменная Х₂ исключится из второго уравнения. Потом исключим Х₂ и из первого.

Роль бортового компьютера поручим микрокалькулятору. Прежде всего разделим на 3 все коэффициенты третьего уравнения. Получим:

$0.666667 X_1 + X_2 + 0.333333X_4=4\hspace{3em}(8)$

теперь вычтем из его второго — 1 ; «-»; 0.666667;=.

На индикаторе появится число 0.333333. Наша система уравнений примет такой вид:
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ ,
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,ㅤㅤㅤㅤ(9)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,

Теперь все переменные, кроме базисных — Т, Х₃ и Х₂,— полагаем равными 0 и получаем: Т=40, Х₃=1, Х₂=4. Это уже неплохо: 40 часов полета. Но можно сделать и лучше. В первом уравнении коэффициент при Х₁ отрицателен, значит, вводя в опорный план эту переменную, можно увеличить Т. А для этого еще раз проделаем подобные вычисления, исключим Х₁ из первого и третьего уравнений, а во втором коэффициент сделаем равным 1. Вот что получится:
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ(10)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,

Отсюда ясно, что если залить 3 л А-7 и 2 л А-10, тогда наш космолет сможет летать 41 час. Пора давать задание роботу- заправщику.

Помогают графики

Задача, которую мы решили, не случайно названа задачей линейного программирования.

Дело в том, что все переменные входят в уравнения и неравенства в первой степени, или, как говорят математики, линейно. А теперь давайте посмотрим, не поможет ли нам график в решении задачи линейного программирования. Только прежде условимся, что оси координат мы будем называть не X и У, а Х₁ и Х₂. Давайте возьмем одно из ограничений нашей задачи $X_1+X_2 \le 5$ и найдем на координатной плоскости те точки, которые ему удовлетворяют (считая, что X₁ и Х₂ больше нуля). Сначала рассмотрим равенство X₁+X₂=5. Построим график этой линии. Для этого найдем две точки: если Х₁=0, то Х₂=5 (точка А), и наоборот, X₁=5, а Х₂=0 (точка В). Соединим точки А и В (см. рис.). Неравенству задачи удовлетворяют точки, лежащие внутри треугольника ОАВ. Координаты каждой из них определяют величины переменных Х₁ и Х₂. Аналогично проведем прямую CD, определяемую вторым ограничением (2X₁+3X₂=12). Она пересекает АВ в точке Е. Любая точка внутри или на границе четырехугольника ОСЕВ представляет возможное решение нашей задачи. Обратите внимание: точка Е как раз отвечает наилучшему, оптимальному решению. Случайно ли это?

Надеемся, что вы поняли суть графического решения задачи линейного программирования. К сожалению, этот способ хорошо работает только при малом количестве переменных, в самых простейших задачах. В реальной ситуации, когда переменных много, компьютеру приходится отыскивать оптимальное решение, переходя от одной к другой грани огромного тысячегранного тела. Процедура эта медленная, и если число переменных превышает 15—20 тысяч, то симплекс-метод, по словам математиков, «выдыхается». Недавно 25-летний математик Нарендре Кармакар нашел новый способ решения задачи линейного программирования, при котором компьютер тратит гораздо меньше времени, чем при традиционном симплекс-методе. Программа Кармакара часть из возможных решений сразу отбрасывает, не тратя время на их просмотр, и после каждого шага деформирует многогранник.

Сам математик сравнил свой способ с оригами — японским искусством складывания бумажных фигур, когда листки бумаги сгибают и складывают так, что искомая грань — а в нашем случае оптимальное решение — оказывается в центре фигуры.

Во саду ли, в огороде…

И здесь может помочь линейное программирование. Представьте себе, что ваш пришкольный участок площадью S вы решили засеять тремя культурами (какие это культуры конкретно, неважно). Урожайность первой— У₁ кг/м², второй — У₂ кг/м² и третьей — У₃ кг/м². Под первую надо внести Р₁ кг удобрений на м“, под вторую — Р₂ и под третью — Р₃, а всего вы имеете П кг удобрений. Постарайтесь найти посевные площади под каждой культурой так, чтобы урожай был наибольшим. При этом не забудьте о возникающих ограничениях. Составьте задачу линейного программирования, задайтесь конкретными цифрами и попробуйте ее решить. Какие еще задачи на отыскание наилучшего решения вы можете придумать?

С. ВОЛКОВ

Рисунки Г. ЗАСЛАВСКОЙ

3. Комментарий, 37 лет спустя (немного моей критики)

Первое, и самое главное: одна из самых частых проблем, при объяснении любых разделов математики кому бы то ни было — мотивационная. Грубо говоря, очень трудно объяснить, например, что такое определитель матрицы, если человек не понимает, зачем ему нужно это знать. Довольно быстро объяснение станет просто нагромождением информации. Чтоб этого не было, нужно всегда связывать объяснение математических понятий с какими-то проблемами из реальной жизни. Т.е. должна быть какая-то зацепка, связь с реальной жизнью. И вот тут автор статьи и художница — большие молодцы. Формулировка задачи, иллюстрации, упоминание компьютера в самом начале, где бортовой компьютер говорит, что топлива — нуль — создают хороший мотивационный фон. Первый раз я прочитал эту статью, когда пошёл в первый класс. Ничего не понял, но мотивирующий осадок остался… Было понимание, что я пропустил что-то важное, очень интересное и нужное. Пока учился в школе — несколько раз возвращался к этой статье, пытаясь её понять. Т.е. с побудительной частью статьи — всё отлично.

Но давайте теперь поставим себя на место школьника (допустим, десятиклассника обычной, не математической школы, читающего эту статью в 1985 году). «Линейное программирование» и «симплекс-метод» — таких слов десятиклассник скорее всего никогда не слышал. Более того, статья выходит в рубрике «ЭВМ в твоих руках», в ней упоминается компьютер, расчёты предполагается делать с помощью микрокалькулятора. У ребёнка того (да и нашего) времени в таком контексте слово «программирование» ассоциируется исключительно с написанием программы для компьютера. Более того, номер журнала свёрстан таким образом, что там, где размещена эта статья, идёт врезка следующего содержания:

На врезке объясняется, что такое программа, что такое цикл… Но линейное программирование к такому программированию,которое подразумевает написание программ с циклами не имеет никакого отношения! Здесь такая комбинация терминов очень легко может ввести читателя в заблуждение. Более того, иногда под линейно исполняемыми программами подразумевают программы, которые исполняются последовательно шаг за шагом, т.е., например, когда у нас есть планировщик операционной системы реального времени, который позволяет всю логику программы разбить на отдельные потоки выполнения, каждый из которых выполняется линейно, и в то же время сами потоки выполняются как будто бы параллельно. (Т.е. это вообще другая степь, относящаяся к реализации параллелизма исполнения в некоторых программах).

Итак, в этом месте для лучшего понимания нужно прямо объяснить значение термина линейное программирование:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств. Определение взято из поста @andron2303
А что такое экстремальная задача? Это задача на нахождение таких значений переменных, при которых какая-то функция (обычно называемая целевой функцией) принимает своё либо максимальное, либо минимальное значение. А максимальное или минимальное — это зависит от самой функции. В одних случаях это будет максимальное (как в нашей нынешней задаче), в других случаях мы можем пытаться минимизировать целевую функцию (например, если она соответствует штрафу или ошибке).

Таким образом, в выражении линейное программирование слово программирование гораздо ближе к такому значению слова «программа» как «программа партии, по обеспечению населения товарами народного потребления», чем к значению, «программа, как реалиация какого-то алгоритма». Программа в данном случае программа — это указание, сколько и какого топлива надо заправить.
Далее… А можно ли решать данную задачу с помощью ЭВМ? Да конечно можно… И для этого нужно описать алгоритм, который можно было бы запрограммировать. Можно ли сказать, что в статье такой алгоритм приводится? С натяжкой. Да, алгоритм объясняется, но он ни в одном месте он не приведён полностью, от начала до конца, а как бы распределён по всей статье. И тут получается, что упоминание возможности решать задачу с помощью ЭВМ, которое было хорошей мотивацией — оно, к сожалению, может сбивать с толку.

Далее я переформулирую задачу и попробую проанализировать её с точки зрения школьника:
Есть два вида топлива: А7 и А10. Мы заправляем X₁ литров А7 и X₂ литров А10.
Целевая функция:
Ограничения:
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ $X_1+X_2 \le 5$ ,ㅤㅤㅤㅤㅤㅤㅤ(5)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ $2X_1+3X_2 \le 12$ ,

Результат решения задачи: X₁ = 3, X₂ = 2

Внимательный школьник может заметить, что решение, полученное с помощью симплекс-метода полностью соответствует решению системы линейных уравнений
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ ,ㅤㅤㅤㅤㅤㅤㅤㅤ(11)
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ,

т.е. при решении СЛАУ (системы линейных алгебраических уравнений) возникают точно такие же корни, из-за чего у школьника, не знающего что такое симплекс-метод, может возникнуть некорректное понимание, что будто бы симплекс-метод — это просто способ решения СЛАУ с помощью ЭВМ.
Дальше — опаснее!

В части статьи, под названием «Помогают графики», автор приводит такую картинку (рис.6, 8)

и следующий провокационный текст: «Обратите внимание: точка Е как раз отвечает наилучшему, оптимальному решению. Случайно ли это?»

И тут мой внутренний математик хочет просто закричать: «Да, чёрт побери, случайно!». У данного симплекса (четырёхугольника OBEC), тот факт, что точка Е соответствует экстремуму целевой функции — случайность. Ведь, например, если бы топлива назывались не А7 и А10, а, например, А6 (плотностью 2 кг/л) и А11(плотностью 3 кг/л), тогда оптимальным планом было бы залить 4 литра А11, пролетев 44 часа. И это была бы уже точка С на приведённом рисунке.

А если бы топлива назывались А9 (с плотностью 2 кг/л) и А8 (с плотностью 3 кг/л), тогда решением была бы точка B на приведённом рисунке… Т.е мы бы залили 5 литров топлива А9 и пролетели бы 45 часов.

Неслучайность точки Е в данном случае выражается только в том, что какая-то из вершин четырёхугольника ОВЕС обязана быть решением экстремальной задачи. Это вытекает из линейности целевой функции. Неформально это можно выразить так: вот мы взяли начальный план — точку O (когда X₁ и X₂ равны нулю) и дальше, если мы хотим что-то максимизировать или минимизировать — надо идти в какую-то сторону до упора (в сторону, в направлении которой целевая функция — время полёта — возрастает).
При этом, если мы упрёмся в ребро, тогда возможно два варианта:
1) мы упёрлись в ребро не под прямым углом — тогда можно продолжать скользить вдоль ребра, стараясь максимизировать продвижение в заданном направлении.
2) мы упёрлись в ребро под прямым углом — но в этом случае все точки ребра (включая вершины, ограничивающие его) — будут решением задачи.

На рисунке 9 я повторил картинку из оригинальной статьи, добавив зелёным цветом вектор OF. Этот вектор имеет координаты {3.5, 5}, т.е. он сонаправлен с вектором {7, 10}. Из рисунка видно, что угол OKE чуть-чуть больше 90 градусов. Т.е. если бы мы привязали ниточку к грузику и тащили бы его по направлению вектора OF, то когда грузик уперся бы в отрезок CE — он «скатился» бы в точку E.

При этом, если бы целевая функция соответствовала бы топливам А6 и А11, её вектор градиента был бы OG, и тогда грузик «скатился» бы в точку C. А если бы мы заправляли A9 и A8, тогда градиент целевой функции был бы сонаправлен с вектором OH и грузик «скатился» бы точку B.

Из упомянутых выше двух пунктов следует, что в любом случае одна из вершин четырёхугольника (или симплекса, в случае многомерной задачи) будет принадлежать множеству оптимальных планов.

Тут у внимательного школьника опять может возникнуть закономерный вопрос: если решение — одна из вершин четырёхугольника, тогда зачем городить какой-то там симплекс-метод? Ведь можно просто подставить каждую из этих вершин в целевую функцию и узнать, на какой из них достигается максимум! И этот школьник будет очень сильно прав. Именно так и можно поступить, когда мы имеем дело с задачей с двумя переменными и четырьмя ограничениями. Но когда переменных не две, а много и ограничений не 4, а тоже очень много, количество вершин может быть довольно велико. И перебирать их все — может оказаться делом весьма затруднительным даже для компьютера. Поэтому их перебирают по-умному. Выбирают одну вершину, находят ребро, при движении в направлении которого целевая функция возрастает, и двигаются вдоль этого ребра до следующей вершины. Потом находят следующее ребро и т.д, пока не упрутся в вершину, из которой движение по всем рёбрам ведёт только к убыванию целевой функции. Эта последняя вершина и является решением.

Как было бы лучше построить изложение решения данной задачи?

Я бы начал как раз с графического способа решения. С использованием возможностей современных пакетов математического моделирования (я буду использовать Octave), можно было бы написать такой код:

close all; clear all;  % Целевая функция для случая заправки смесью топлив А7 и А10 target_7_10 = @(x1, x2) 7*x1+10*x2;  % Целевая функция для случая заправки смесью топлив А6 и А11 target_6_11 = @(x1, x2) 6*x1+11*x2;  % Целевая функция для случая заправки смесью топлив А9 и А8 target_9_8  = @(x1, x2) 9*x1+8*x2;  % Функция вычисления запаса по массе топлива mass_margin = @(x1, x2) 12-2*x1 -3*x2;  % Функция вычисления запаса по объёму топлива vol_margin  = @(x1, x2) 5 -  x1 -  x2;  % области проверяемых значений для X1 и X2 xx1 = (0:0.01:6); xx2 = (0:0.01:6);  [x1 x2] = meshgrid(xx1, xx2);  % вычисляем запас по объёму vol_margin_values = vol_margin(x1, x2); % обнуляем все значения, в которых запас по объёму отрицательный vol_margin_values(find(vol_margin_values < 0)) = NaN;  % вычисляем запас по массе mass_margin_values = mass_margin(x1, x2); % обнуляем все значения, в которых запас по массе отрицательный mass_margin_values(find(mass_margin_values < 0)) = NaN;  % так выглядят наши ограничения ОДЗ для Х1 и Х2: figure; s1 = mesh(x1, x2, mass_margin_values);  set(s1,'facealpha',0.5); hold on;  s2 = mesh(x1, x2, vol_margin_values); set(s2,'facealpha', 0.5); hold off; xlabel('x1'); ylabel('x2'); zlabel('margin');  % расчитываем целевую функцию values_target_7_10 = target_7_10(x1,x2); % обнуляем целевую функцию там, где нет запаса по массе или по объёму values_target_7_10(find(isnan(vol_margin_values))) = NaN; values_target_7_10(find(isnan(mass_margin_values))) = NaN;  % общий вид целевой функции figure; mesh(x1, x2, values_target_7_10); xlabel('x1'); ylabel('x2'); zlabel('flight time'); view(30,40); title('A7/A10 target function top view');  % теперь посмотрим на целевую функцию, так, чтоб понять, где оптимум X1 figure; mesh(x1, x2, values_target_7_10); xlabel('x1'); ylabel('x2'); zlabel('flight time'); view(0,0); title('x1 optimal value for A7 (when x2 is A10)'); grid minor;  % теперь посмотрим на целевую функцию, так, чтоб понять, где оптимум X2 figure; mesh(x1, x2, values_target_7_10); xlabel('x1'); ylabel('x2'); zlabel('flight time'); view(90,0); title('x2 optimal value for A10 (when x1 is A7)'); grid minor;  % теперь посмотрим как выглядит наш "симплекс" сверху: figure; mesh(x1, x2, values_target_7_10); xlabel('x1'); ylabel('x2'); zlabel('flight time'); view(0,90); title('Shape of the simplex'); grid minor;

И получить вот такую визуализацию (рис. 9):

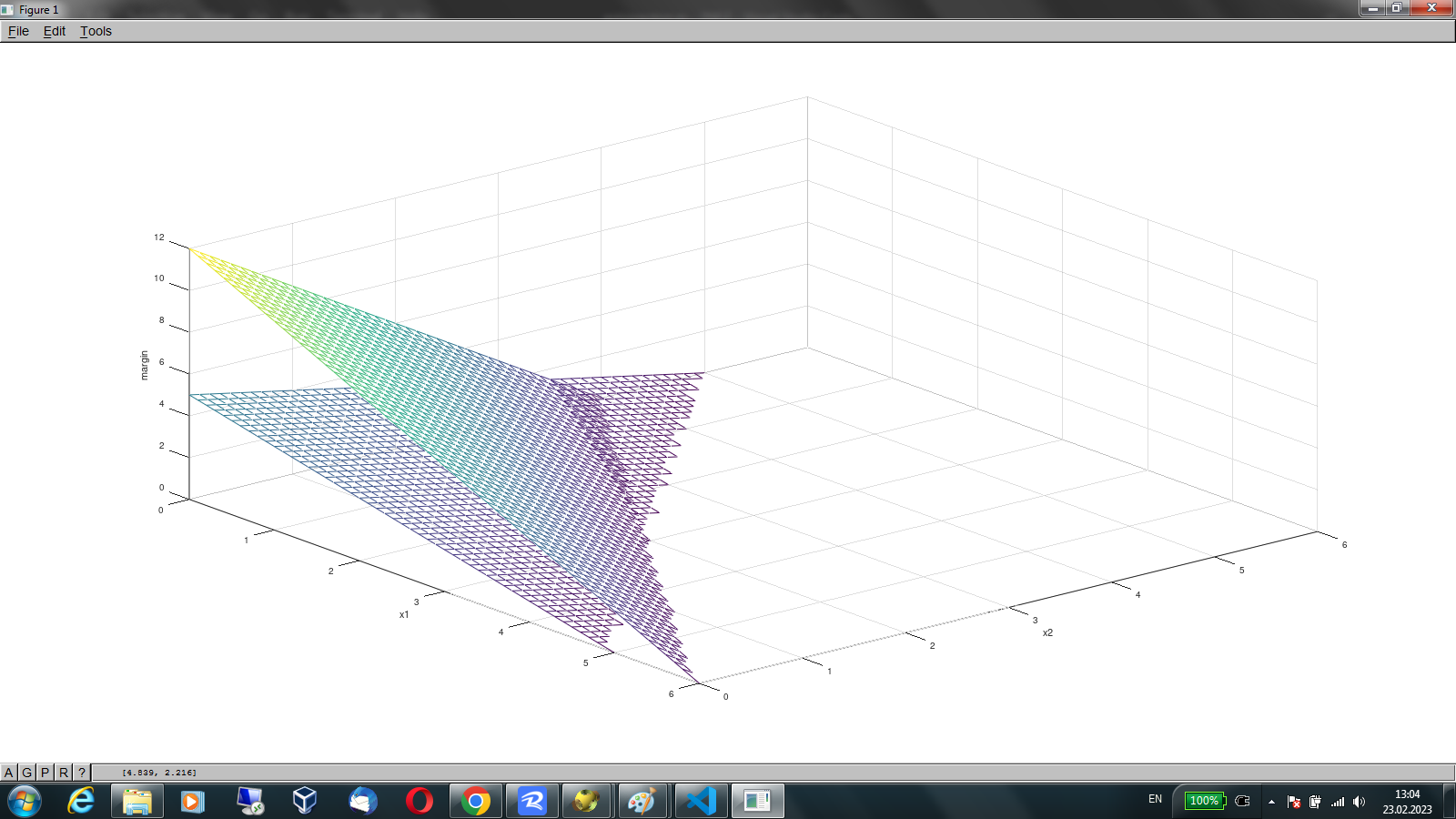
Этот рисунок наглядно изображает область допустимых значений X₁ и X₂. Вертикальная ось — запасы свободных объёма и массы. Область допустимых значений — это та область, в которую покрывают оба треугольника (соответствует четырёхугольнику OBEC на рисунках 6,8).

Следующий рисунок (рис 11) показывает форму «лоскутка» значений целевой функции если мы используем топлива А7 и А10:

Из рисунка не очень понятно, где находится оптимальное значение, т.к. он нарисован в изометрической проекции, поэтому повернём его так, чтоб стало понятно, какие оптимальные значения для X₁ и X₂(рис 12 и 13) :

(на рисунках 12 и 13 наглядно видно, что заливание 4 литров А10 даёт меньшее значение времени полёта, чем когда мы заливаем 2 литра А10, доливая остатки ёмкости бака топливом А7 и видно, что максимум целевой функции достигается именно при X₂ = 2 и X₁ = 3.
А вот так выглядит «симплекс» сверху:

В качестве упражнения для школьников я бы оставил возможность найти графически оптимальный план при условиях, что на заправке есть:
а) топлива А6 и А11
б) топлива А8 и А9
В приведённом скрипте для этого уже всё есть.

После такого графического решения я бы объяснил школьникам, что в случае, когда переменных больше двух, мы будем иметь дело не с плоской, а с объёмной фигурой, и вот эта-то вот объёмная фигура и называется страшным словом симплекс.По сути, симплекс — это любой выпуклый многогранник в N-мерном пространстве. При N=2 многогранник превращается в многоугольник.
Количество граней у такого многогранника равно количеству накладываемых ограничений (а в двумерной ситуации вместо граней будут рёбра многоугольника).

Здесь внимательный школьник задал бы вопрос: но ведь у нас всего 2 ограничения, а сторон у многоугольника 4. Как же так? И я бы ему ответил, что на самом деле в данной задаче 4 ограничения. Просто 2 из них не озвучены в явном виде и предложил бы самому эти два дополнительных ограничения найти (правильный ответ — это ограничения $X_1 \ge 0; X_2 \ge0$ ) и только после такого вот графического введения я бы может быть и предложил бы школьнику одно из описаний симплекс-метода из уже упомянутых выше (раз и два).

Также я бы объяснил детям, что «выдыхание» симплекс-метода для большого числа переменных скорее всего связано особенностью представления вещественных чисел в компьютере и с тем, что компьютер, суммируя одну и ту же последовательность вещественных чисел по-разному (например, начиная с больших чисел и заканчивая малыми и, наоборот, начиная с малых и заканчивая большими) может выдавать сильно разные результаты. Отсюда и может поломаться алгоритм (просто целевая функция может вычисляться некорректно, а это очень важно для не только для нахождения решения, но и для того, чтоб алгоритм не зациклился нигде).

Теперь можно попробовать разобраться и в приведённых в оригинальной статье уравнениях (когда они сгруппированы — читать и разбираться в них должно быть легче):

Уравнения в оригинальной статье (для удобства я вместо десятичных дробей использовал обыкновенные)	Как можно было бы написать, пользуясь алгоритмом, изложенным тут: https://habr.com/ru/post/474286/	Комментарий
ㅤㅤㅤㅤ (1) $X_1 + X_2 \le 5$ ㅤㅤㅤㅤㅤㅤ (5) $2X_1+3X_2 \le 12$ $X_1, X_2 \ge 0$ (этого не было, но подразумевалось)	$X_1+X_2 \le 5$ $2X_1 + 3X_2 \le 12$ $X_1, X_2 \ge 0$	Условия задачи (и хотя в них не говорится о неотрицательности X1 и X2, но, очевидно, это подразумевается.
ㅤ(7.1) ㅤㅤ(7.2) ㅤ(7.3) $X_1, X_2, X_3, X_4 \ge 0$ X3 и X4 — это наш базис сейчас, мы ими можем «играть».	ㅤㅤ\|ㅤX₁ㅤX₂ㅤX₃ㅤX₄ \| _______________________ X₃ㅤ\|ㅤ1ㅤ 1 ㅤ 1 ㅤ 0ㅤ\| 5 X₄ㅤ\|ㅤ2 ㅤ3 ㅤ 0 ㅤ 1ㅤ\| 12 _______________________ Tㅤ\|ㅤ-7ㅤ-10ㅤ 0 ㅤ 0ㅤ\| 0 ведущий столбец X₂ (потому что -10 < -7 ) ведущая строка X₄ (потому что $\frac{12}{3} < \frac{5}{1}$ ) ведущий элемент 3	Теперь у нас уже четыре ограничения вместо двух, но неравенства превратились в уравнения, это и называется канонической формой.
На этом этапе у нас есть 4 переменных (и 4 ограничений) и только 2 уравнения. Из этого следует, что размерность пространства решений равна 4 — 2 = 2. Это означает, что для навигации по этому 2-мерному пространству нам нужны 2 переменных (или вектор из двух компонент). А вектор всегда можно разложить по базису. Но если мы произвольно изменяем 2 из 4 переменных, тогда остальные 2 будут меняться в зависимости от тех двух, которые мы меняем как хотим.Именно поэтому в симплекс-методе и вводится термин «базис». Базис включает в себя те переменные, которые мы собираемся менять произвольно, переменные, не входящие в базис, будут такими, какими получатся. В нашем случае, базисом должны в конечном итоге стать X₁ и X₂ , но в начале мы берём X₁ и X₂ равными 0. А в базис вводим X₃ и X₄. (А не X₃, X₄ и T, как говорится в оригинальной статье).
(9.3) = (7.3) : 3 (9.2) = (7.2) — (9.3) (9.1) = (7.1) + 10*(9.3)		избавляемся от X₂ в уравнении 7.2
$\frac{2}{3} X_1 + X_2 + \frac{1}{3}X_4=4$ (9.3) $\frac{1}{3}X_1+X_3-\frac{1}{3}X_4 = 1$ (9.2) $T-\frac{1}{3}X_1+\frac{10}{3}X_4 = 40$ (9.1)	ㅤㅤ\|ㅤX₁ㅤX₂ㅤX₃ㅤX₄ㅤ\| _______________________ X₃ㅤ\|ㅤ1/3ㅤ0ㅤ 1ㅤ-1/3ㅤ\| 5 X₄ㅤ\|ㅤ2/3ㅤ0 ㅤ1ㅤ 1/3ㅤ\| 4 _______________________ T ㅤ\| -1/3 ㅤ 0 ㅤ 0 ㅤ10/3 \| 0
(10.1) = (9.1) + (9.2) (10.2) = (9.2) * 3 (10.3) = (9.3) — 2*(9.2)
,ㅤㅤ(10.1) ,ㅤㅤ(10.2) $X_2-2X_3-\frac{1}{3}X_4 = 2$ ㅤ(10.3) Здесь нетрудно заметить, что уравнение (10.3) должно выглядеть как: , т.е. в оригинальной статье была опечатка, хотя она и не влияет на результат.	ㅤㅤ\|ㅤX₁ㅤX₂ㅤX₃ㅤX₄ㅤ\| _______________________ X₁ㅤ\|ㅤ1 ㅤ 0 ㅤ 3 ㅤ -1ㅤ\| 3 X₂ㅤ\|ㅤ0 ㅤ 1 ㅤ-2 ㅤ 1ㅤ \| 2 _______________________ T ㅤ\|ㅤ 0 ㅤ 0 ㅤ 1 ㅤ 3 ㅤ\| 41 Видим, что в последней строке нет отрицательных коэффициентов, значит мы не можем увеличить значение целевой функции, значит данный план является оптимальным.	Здесь коэффициенты при X₃ и X₄ не играют уже никакой роли, потому что сами X₃ и X₄ равны 0.

4. И всё-таки, как решить данную задачу с помощью компьютера?

Я бы рекомендовал использовать какой-нибудь язык численного моделирования (Matlab, Octave, R, Python). Поскольку мне ближе Octave, я приведу пример для него.

octave:68> c = [7 10]'; octave:69> A = [1 1; 2 3]; octave:70> b = [5 12]; octave:71> [xopt fmax] = glpk(c, A, b); octave:72> xopt xopt =     3.0000    2.0000  octave:73> fmax fmax = 41 octave:74>

5. Заключение

Здесь я должен ещё раз обратить внимание на то, что оригинальная статья — это шедевр, несмотря на указанные мной недостатки. Нормальный учитель математики, физики, информатики, химии вполне мог бы разобраться и объяснить метод детям. Ну и важно понимать, что в тех условиях 1985 года, когда не было возможности использовать $\LaTeX$ , когда компьютеры были редкостью, когда никакого Octave или Python не было и в помине, а формат журнала не позволял растечься мыслею по древу, написать то, что было написано — это огромный шаг вперёд…

ссылка на оригинал статьи https://habr.com/ru/post/718460/